تخطيط (رياضيات)
الاستخطاط أو التخطيط Linearization في الرياضيات هي عملية الهدف منها تقريب معادلة أو نظام غير خطي بنظام خطي و ذلك لما تحمله النظم الخطية من سهولة في المعالجة. تستخدم هذه الطريقة في العديد من فروع العلوم مثل الهندسة التطبيقية، الفيزياء، الاقتصاد، وعلم البيئة.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
استخطاط دالة
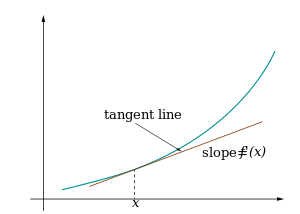
إن استخطاط دالة هو عبارة عن خط مستقيم يستخدم في أغراض تبسيط الحساب. عادة يتم استخطاط أي دالة عند نقطة باستخدام ميل الدالة عند ، وذلك بافتراض أن f(x) هو دالة مستمرة على المجال وأن قريبة جداً من النقطة .
يعطى الاستخطاط لدالة مستمرة عند النقطة بالمعادلة:
حيث , . مشتق الدالة هو ، وميل الدالة عند النقطة هو .
مثال
على سبيل المثال، قد تعلم أن ، ولكن وبدون آلة حاسبة ما الذي يمكن أن يكون تقريباً جيداً للقيمة ؟
من أجل إيجاد قيمة ، نستخدم معرفتنا بأن . وعندها يكون استخطاط عند النقطة is ، لأن الدالة تعرف ميل الدالة عند . وبتعويض قيمة ، يكون الاستخطاط عند 4 مساوياً . وفي هذه الحالة ، إذاً is يساوي تقريباً . القيمة الحقيقية قريباً جداً من 2.00024998, وبهذا يكون تقريب الاستخطاط ذو خطأ أقل من 1 بالمليون بالمائة.
مواضيع متعلقة
- مبرهنة الاستخطاط Linearization theorem
- مصفوفة جاكوبي
- متسلسلة تايلور



![{\displaystyle [a,b]}](https://www.marefa.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

















