تحويل لورنتس

في الفيزياء، تحويل لورنتس Lorentz transformation أو تحويل لورنتس-فتسجرالد Lorentz-Fitzgerald transformation يصف كيف أنه، حسب نظرية النسبية الخاصة، قياسات مختلفة في المكان والزمان من مراقبَين مختلفَين يمكن تحويلها إلى قياسات الاطار المرجعي الآخر. أي أن التحويل يُستخدم لتحويل الإحداثيات المكانية والزمانية (أو بشكل عام أي متجه رباعي الأبعاد) في إطار مرجعي عطالي س إلى الإحداثيات الأربعة في إطار مرجعي آخر ع. تعتمد تحويلات لورنتس على على وجود سرعة قصوي في الكون لا يمكن للأجسام تعديتها، ألا وهي سرعة الضوء c في الفراغ.
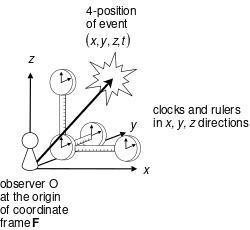
فاذا حصل الحدث في الإطار المرجعي العطالي (مختبر) س بالإحداثيات وشوهد الحدث نفسه من "المختبر" ع بالإحداثيات فيحتم مبدأ النسبية (تساوي القوانين الطبيعية في س و ع ) مع اعتبار سرعة الضوء c هي أقصي سرعة في الكون للأجسام ولانتقالم الطاقة، فتوصل لورنتس إلى التحويلات الآتية :
حيث :
- x و y و z هي إحداثيات المكان ،
- t إحداثية الزمن ،
- v سرعة الجسم
- سرعة الضوء في الفراغ .
و
- يدعى معامل لورنتس
كما توجد معادلات تحويل عكسية تسمى معادلات لورنتس العكسية.
تحويل لورنتس لإطارات في نسق عياري
الرفع في اتجاه x

Top: frame F' moves at velocity v along the x-axis of frame F.
Bottom: frame F moves at velocity −v along the x'-axis of frame F'.[1]
حيث:
- v هي السرعة النسبية بين الإطارين في اتجاه x،
- c هي سرعة الضوء،
- is the Lorentz factor (Greek lowercase gamma),
- (Greek lowercase beta), again for the x-direction.
The use of β and γ is standard throughout the literature.[2] For the remainder of the article - they will be also used throughout unless otherwise stated. Since the above is a linear system of equations (more technically a linear transformation), they can be written in matrix form:
According to the principle of relativity, there is no privileged frame of reference, so the inverse transformations frame F′ to frame F must be given by simply negating v.
Note that here, the same value of γ remains unchanged.
الرفع في اتجاهات y أو z
The above collection of equations apply only for a boost in the x-direction. The standard configuration works equally well in the y or z directions instead of x, and so the results are similar.
وللاتجاه y:
summarized by
where v and so β are now in the y-direction. For the z-direction:
summarized by
where v and so β are now in the z-direction.
The Lorentz or boost matrix is usually denoted by Λ (Greek capital lambda). Above the transformations have been applied to the four-position X,
The Lorentz transform for a boost in one of the above directions can be compactly written as a single matrix equation:
الرفع في أي اتجاه
الشكل المتجهي
For a boost in an arbitrary direction with velocity v, it is convenient to decompose the spatial vector r into components perpendicular and parallel to v:
so that
where · denotes the dot product, see also orthogonality for more information. Then, only time and the component in the direction of v;
are "warped" by the Lorentz factor:
- .
The second of these can be written as:
Collecting parallel and perpendicular components of r into one equation Starting from the transformation for r:
adding to eliminate :
now adding to eliminate :
Since and v are parallel we can write
in which v/v is a dimensionless unit vector pointing in the same direction as , and this leads to
This method applies for any Lorentz transformation written in an analogous way: components of the 3-vector parallel and perpendicular to the relative velocity.
الأشكال المصفوفية
تلك المعادلات يمكن التعبير عنها في شكل block matrix كالتالي
where I is the 3×3 identity matrix and β = v/c is the relative velocity vector (in units of c) as a column vector - in cartesian and tensor index notation it is:
βT = vT/c is the transpose - a row vector:
and β is the magnitude of β:
More explicitly stated:
The transformation Λ can be written in the same form as before,
which has the structure:[3]
and the components deduced from above are:
حيث δij هي دلتا كرونكر، and by convention: Latin letters for indices take the values 1, 2, 3, for spatial components of a 4-vector (Greek indices take values 0, 1, 2, 3 for time and space components).
Note that this transformation is only the "boost," i.e., a transformation between two frames whose x, y, and z axis are parallel and whose spacetime origins coincide. The most general proper Lorentz transformation also contains a rotation of the three axes, because the composition of two boosts is not a pure boost but is a boost followed by a rotation. The rotation gives rise to Thomas precession. The boost is given by a symmetric matrix, but the general Lorentz transformation matrix need not be symmetric.
جمع رفعين

The composition of two Lorentz boosts B(u) and B(v) of velocities u and v is given by:[4][5]
- ,
حيث
- B(v) is the 4 × 4 matrix that uses the components of v, i.e. v1, v2, v3 in the entries of the matrix, or rather the components of v/c in the representation that is used above,
- is the velocity-addition,
- Gyr[u,v] (capital G) is the rotation arising from the composition. If the 3 × 3 matrix form of the rotation applied to spatial coordinates is given by gyr[u,v], then the 4 × 4 matrix rotation applied to 4-coordinates is given by:[4]
- gyr (lower case g) is the gyrovector space abstraction of the gyroscopic Thomas precession, defined as an operator on a velocity w in terms of velocity addition:
- for all w.
The composition of two Lorentz transformations L(u, U) and L(v, V) which include rotations U and V is given by:[6]
Rapidity
The Lorentz transformation can be cast into another useful form by defining a parameter ϕ called the rapidity (an instance of hyperbolic angle) such that
so that
Equivalently:
Then the Lorentz transformation in standard configuration is:
التعبيرات الزائدية
From the above expressions for eφ and e−φ
ولذلك،
الدوران الزائدي للإحداثيات
Substituting these expressions into the matrix form of the transformation, we have:
وبذلك، فإن تحويل لورنتس يمكن رؤيته كـدوران زائدي للإحداثيات في فراغ منكوڤسكي، حيث المتغير ϕ يمثل الزاوية الزائدية للدوران، التي يكثر الاشارة إليها بإسم rapidity. وأحياناً يُصوّر هذا التحويل بمخطط منكوڤسكي، كما هو مبين في بداية المقال.
تأريخ
فكر لورنتس في تلك التحويلات بعد أن أتت تجربة ميكلسون ومورلي عام 1881 بنتيجة غير متوقعة . فقد أجرى العالمان "ميكلسون" و "مورلي " تجربتهما الشهيرة لتعيين سرعة الضوء فيما كان يسمى "أثير" ، اعتقد العلماء آنذاك بوجوده في الفراغ لتفسير انتقال الضوء فيه ، مثلما بنتقل الصوت في وسط مثل الهواء أو الماء (لا ينتقل الصوت في الفراغ) . وكانت تجربة ميكلسون ومورلي مبنية على فكرة تعيين سرعة الضوء في اتجاهين متعامدين أحدهما في اتجاه حركة الأرض في دورانها حول الشمس . وباعتبار أن الأرض تسبح في "أثير" بسرعة 30 كيلومتر في الثانية ، فكان لا بد وأن تختلف سرعة الضوء في اتجاهين عكسيين أو في اتجاهين متعامدين . ولكن لم يظهر في التجربة أي اختلاف في سرعة الضوء، بمعنى أنه لا يوجد أثير ينتقل بواستطه الضوء. وكانت تلك النتيجة غير متوقعة وحيرت العلماء.
فكانت فكرة لورنتس للخروج من ذلك المأزق أنه ربما يحدث في تجربة ميكلسون تقلص في طول المسافة التي كان يقيسها ميكلسون ومورلي في تجربتهما ، وأتت تحويلاته فعلا بتقلص لتلك المسافة متعلقا بالنسبة بين سرعة الأرض v في الفضاء وسرعة الضوء c. وفي عام 1905 صاغ ألبرت أينشتاين النظرية النسبية الخاصة -وكان عمره 25 سنة - وفسر مسألة انتشار الضوء على أساس أن الضوء هو أقصي سرعة في الكون و أنها ثابتة في الفراغ لا تتغير . وتتضمن النظرية النسبية تحويلات لورينتز .
في حياتنا اليومية نتعامل مع سرعات بطيئة جدا بالنسبة لسرعة الضوء ، وسرعة الضوء كبيرة جدا فهي تبلغ 300.000 كيلومتر في الثانية (أي يلف شعاع كهرومغناطيسي مثل الضوء حول الأرض سبع مرات في ثانية واحدة) . لذلك لا نلاحظ الـأثيرات النسبية (مثل تقلص الأطوال ، إبطاء زمني ، أو تراقص السرعات) عند تلك السرعات البطيئة ، وتصلح في تلك المسائل استخدام تحويل گاليليو بين إطارين مرجعين (وهذا هو ما تعودناه). أما عندما تقترب سرعة الجسم من سرعة الضوء فلا بد من استخدام تحويلات لورنتس، فتحويلات گاليليو هي تقريبية بمقارنتها بتحويلات لورنتس، ولا يصح استخدام تحويل گاليليو في سرعات كبيرة.
تغير الكتلة مع زيادة السرعة
تعودنا على ان الكتلة لا تتغير بزيادة السرعة . ويعود ذلك إلى أننا نعتبر أن السرعة تتزايد بتزايد الزمن الذي تؤثر فيه قوة على الجسم باعتبار تلك القوة ثابتة. ويقوم هذا الاستنتاج على القانون المعتاد لتجميع السرعات .ولكن النظرية النسبية الخاصة تقول أنه يوجد حد اقصى للسرعات ، أي اننا لا نستطيع في جميع الاحوال تطبيق قانون جمع السرعات المعتاد .
كيف نستطيع تعيين سرعة جسم بعد الثالنية الثانية لتأثير القوة عليه؟ إننا نجمع السرعتين ، السرعة التي اكتسبها خلال الثاتية الأولى مضافا إليها السرعة التي اكتسبها الجسم خلال الثانية الثانية وذلك طبقا لقانون جمع السرعات العادي . ولكننا نستطيع اجراء ذلك إلى ان نقترب من سرعة الضوء . وفي تلك الحالة لا يصح استخدام القانون المعتاد . فعندما نجمع السرعات طبقا للنطرية النسبية نجد انها تعطي سرعة اقل من السرعة التي يحسبها القانون العادي . وهذا معناه أن السرعات العالية لا تتناسب طرديا مع الزمن الذي تؤثر خلاله القوة على الجسم ، وإنما يتم ذلك أبطأ بكثير. ويتضح لنا ذلك بمعرفة وجود حد أقصى للسرعات .
فعندما تقترب سرعة جسم تحت تاثير قوة من سرعة الضوء فانها تزداد أقل فأقل ، بحيث لا تتعدى الحد الأقصى للسرعات . وطالما اعتبرنا ان سرعة الجسم تتناسب تناسبا طرديا مع زمن تاثير القوة على الجسن يحق لنا اعتبار ان الكتلة لا تعتمد على السرعة . ولكن عندما تقترب سرعة الجسم من سرعة الضوء فلا يصبح هذا التناسب بين الزمن والسرعة قائما ، وتصبح الكتلة معتمدة على السرعة . ونظرا لأن زمن التسريع يمكن أن يطول إلى مالانهاية بينما لن تتعدى سرعة الجسم الحد الاقصي للسرعة ، فنستنتج من ذلك أن الكتلة تزداد بزيادة السرعة ، وتتخذ قيمة لا نهاية عندما تصل سرعة الجسم سرعة الضوء.
وتبين الحسابات أن تغير كتلة الجسم بازدياد سرعته هو تغير ينم بنفس معدل تقلص طوله طبقا لمعادلة لورنتس. فإدا كان جسم يتحرك بسرعة 240.000 كيلومتر في الثانية تصل كتلته إلى 6و1 من كتلته في حالة السكون (سرعة الضوء تبلغ 300.000 كيلومتر في الثانية).
فكان من الطبيعي أنه عند تعاملنا مع سرعات اقل بكثير من سرعة اضوء أن نعتبر أن كتلته ثابتة لا تعتمد على السرعة ، مثلما نعتبر ان طوله لا يعتمد على سرعته . وقد اختبرت زيادة كتلة الإلكترون مع زيادة سرعته عمليا وثبتت تلك الحقيقة . فقد أصبح معتادا تسريع الالكترونات إلى سرعات قريبة من سرعة الضوء . ووصلنا إلى تسريع الإلكترونات في بعض معجلات الجسيمات إلى سرعة أقل 30 كيلومتر في الثانية من سرعة الضوء . ويمكن للفيزيائيين مقارنة كتلة الإلكترون الساكن بكتلة الإلكترون السريع . وتتفق نتائج التجارب على أن الكتلة تزداد بزيادة سرعة الجسم طبقا لمعادلات لورنتس، ويتفق ذلك تماما مع مبدأ النسبية.
انظر أيضا
- Ricci calculus
- Electromagnetic field
- تحويل گاليليو
- Hyperbolic rotation
- Invariance mechanics
- Lorentz group
- Principle of relativity
- Velocity-addition formula
- Algebra of physical space
- Relativistic aberration
- Prandtl–Glauert transformation
المصادر
- ^ University Physics – With Modern Physics (12th Edition), H.D. Young, R.A. Freedman (Original edition), Addison-Wesley (Pearson International), 1st Edition: 1949, 12th Edition: 2008, ISBN (10-) 0-321-50130-6, ISBN (13-) 978-0-321-50130-1
- ^ Relativity DeMystified, D. McMahon, Mc Graw Hill (USA), 2006, ISBN 0-07-145545-0
- ^ خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةGravitation, J.A. Wheeler 1973 - ^ أ ب Ungar, A. A. (1989). "The relativistic velocity composition paradox and the Thomas rotation". Foundations of Physics. 19: 1385–1396. Bibcode:1989FoPh...19.1385U. doi:10.1007/BF00732759.
- ^ Ungar, A. A. (2000). "The relativistic composite-velocity reciprocity principle". Foundations of Physics. Springer. 30 (2): 331–342. قالب:Citeseerx.
- ^ eq. (55), Thomas rotation and the parameterization of the Lorentz transformation group, AA Ungar - Foundations of Physics Letters, 1988































![{\displaystyle {\begin{aligned}\mathbf {r} '&=\gamma \mathbf {r} -\gamma \mathbf {v} t+[(1-\gamma )\mathbf {r} _{\bot }{\color {Violet}+(1-\gamma )\mathbf {r} _{\parallel }}]{\color {Violet}-(1-\gamma )\mathbf {r} _{\parallel }}\\&=\gamma \mathbf {r} -\gamma \mathbf {v} t+(1-\gamma )\mathbf {r} +(\gamma -1)\mathbf {r} _{\parallel }\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6777f57cf6f9d8e2233e67e9552115cad5562ea2)











![{\displaystyle B(\mathbf {u} )B(\mathbf {v} )=B\left(\mathbf {u} \oplus \mathbf {v} \right)\mathrm {Gyr} \left[\mathbf {u} ,\mathbf {v} \right]=\mathrm {Gyr} \left[\mathbf {u} ,\mathbf {v} \right]B\left(\mathbf {v} \oplus \mathbf {u} \right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8da53c00afa6c8762037a5a27409eae309dc96ba)

![{\displaystyle \mathrm {Gyr} [\mathbf {u} ,\mathbf {v} ]={\begin{pmatrix}1&0\\0&\mathrm {gyr} [\mathbf {u} ,\mathbf {v} ]\end{pmatrix}}\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8043bbcbbd9099d8e13a97b2e0f06cc35392e913)
![{\displaystyle {\text{gyr}}[\mathbf {u} ,\mathbf {v} ]\mathbf {w} =\ominus (\mathbf {u} \oplus \mathbf {v} )\oplus (\mathbf {u} \oplus (\mathbf {v} \oplus \mathbf {w} ))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f3460810e6aa6eac8b33ddfa0b3008bb5ebd153)
![{\displaystyle L(\mathbf {u} ,U)L(\mathbf {u} ,V)=L(\mathbf {u} \oplus U\mathbf {v} ,\mathrm {gyr} [\mathbf {u} ,U\mathbf {v} ]UV)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10f12a6f40c6d0c69a5e1ab011fcb61b8209a34e)


![{\displaystyle \phi =\ln \left[\gamma (1+\beta )\right]=-\ln \left[\gamma (1-\beta )\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47a501800747e94121c6b8c882307d341bd63e8d)




