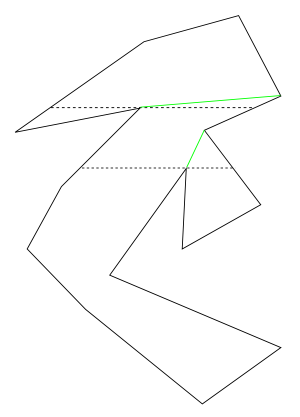
تثليث مضلع
التثليث المضلع، في علم الهندسة الحاسوبية، هو تقسيم مضلع إلى مجموعة من المثلثات.
تعريف
أن تثليث مضلع P هي عملية تجزئته إلي مثلثات لا تتداخل فيما بينها والذي مجموعها باتحادها (union) هو P بالذات. في التعريف الصارم، يشترط أن تكون زوايا (vertices) المثلثات واقعة على زواية المضلع. أما في التعريف المسهل، فيمكن لزوايا المثلثات أن تكون في أي مكان على الأضلاع أو في داخل المضلع.
التثليت هي حالات خاصة من المخططات البيانية للخطوط المستقيمة (planar straight-line graph).
المضلع المحدب هي حالة سهلة لتثليثها في الزمن الخطي. يكفي رسم خطوط من كل زاوية إلى الزاوية الأخرى في المضلع. وأظهر برنارد شازيل[1] في عام 1991 إمكانية تثليث المضلعات البسيطة في الزمن الخطي. لكن خوارزميته (algorithm) معقدة والرياضيون ما زالوا يبحثون عن حلول أسهل.
طرق التثليث
طريقة تقليم الأذن
إحدى الطرق لتثليث مضلع هي بالاعتماد على خاصية بأن لكل ضلع: على الأقل، "أذنتين" اثنين. والأذن في المضلع هو مثلث بحيث ضلعيه مرسومين على حد المضلع بينما الضلع الثالث داخل المضلع بشكل تام. وأسلوب تحديد المثلثات يتم بتحديد كل أذن ثم أزالت جزئها من المضلع، وتكرار العملية حتى يبقى مثلث واحد فقط. هذه الطريقة سهلت التحقيق إلا أنها ليست المثلى إلا أنها تفشل في حال ضلع مفرغ. بعضهم يسميها تشذيب الأذن (ear trimming) و البعض يسميها طريقة طرح الأذن (Subtracting ears method).
طريقة استعمال مضلع رتيب
المضلع الرتيب هو شكل من المضلعات لا يخترقه أي خط مستقيم في أكثر من نقطتين. ولتقطيع مضلع بسيط إلى مضلعات رتيبة، اتبع الخطوات التالية: ارسم خط ماسح (sweep line) أما عمودي أو أفقي. إذا كان الزوايا على نفس جهة الخط، فامسح الخط التالي في الجهة المقابلة. قسم المضلع بين النقطة الأصلية وأي من النقاط عليها.
انظر أيضاً
مراجع
- أماتو, نانسيM.; غودريدج, مايكل; Ramos, أدغارA. (2001), "خوارزمية عشوائية لتثليث مضلع بزمن خطي", Discrete & الهندسة الحاسوبية 26 (2): 245–265, doi:, ISSN 0179-5376, http://parasol.tamu.edu/publications/abstract.php?pub_id=185
- فورنيير, أ; مونتونو, د (1984), "تثليث مضلع ومسائل مماثلة", ACM Transactions on Graphics 3 (2): 153–174, doi:, ISSN 0730-0301
- مارك دو بيرغ وأخرون (2000). الهندسة الحاسوبية. Springer-Verlag. ISBN 3-540-65620-0. الفصل الثالث: تثليث المضلع: pp.45-61.