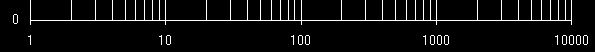المرشحات وتمثيل بود
المرشحات وتمثيل بود
يعد تمثيل بود أساسيا في فهم العلاقة بين دخل الدارة وخرجها من أجل التواترات المختلفة للتيار. سنحاول بداية دراسة العلاقة بين دخل دارة وخرجها من خلال تابع النقل، ثم سننتقل بعدها لدراسة تفصيلية لمخططات بود.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
استجابة دارة RC تسلسلية
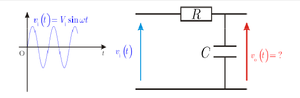
لتكن لدينا دارة RC المبينة في الشكل. نطبق على مدخل هذه الدارة فلطية جيبية نبضها وسعتها العظمى Vi بحيث:
وبشكل عقدي:
سنحاول الآن إيجاد استجابة الدارة أي الفلطية بين طرفي المكثفة vc، بدلالة الدخل vi.
نعلم أن الاستجابة ستكون أيضا تابعا جيبيا من الشكل:
وبشكل عقدي:
يمكننا الحصول على vo بسهولة من خلال تطبيق قانون مجزئ الفلطية:
الآن لنتحدث عما يسمى بتابع النقل. هو في الحقيقة التابع الموضوع بين قوسين أعلاه، فهو يعبر عن نسبة إشارة الخرج العقدية إلى إشارة الدخل العقدية.
إذا في دارة RC المدروسة، سيكون تابع النقل: وهو تابع للنبض المطبق، لذلك فهو يمكننا من دراسة نسبة الدخل إلى الخرج من أجل التواترات المختلفة المطبقة على الدارة.
نلاحظ أن طويلة تابع التحويل هي نسبة سعة الخرج إلى سعة الدخل، أي:
أما طور تابع التحويل فهو طور إشارة الخرج بعد طرح طور إشارة الدخل. وبما أن طور الدخل يساوي الصفر، فطور تابع التحويل هو نفسه طور إشارة الخرج .
نلاحظ وجود المقدار في علاقة تابع النقل، لذلك ومن أجل التبسيط، سنفرض أن: فيكون:
سنقوم الآن بدراسة كل من طويلة وطور تابع النقل للدارة RC.
أولا: طويلة تابع نقل الدارة RC
طويلة تابع النقل في هذه الحالة:
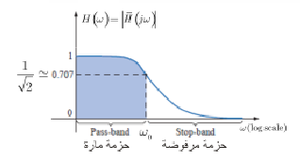
نقوم برسم المخطط البياني لتابع الطويلة. نلاحظ أنه من أجل قيم صغيرة فإن قيمة H قريبة جدا من الواحد، أي أن سعة فلطية كل من الدخل والخرج متقاربتان جدا. وهذا تماما ما يحصل عندما يكون لدينا تيار مستمر (حيث ) فتلعب المكثفة دور القاطعة، فتكون الفلطية على طرفيها مساوية لفلطية الدخل.
نلاحظ من المخطط أيضا أن قيم H تتناهى إلى الصفر من أجل تردداتكبيرة جدا. ففي هذه الحالة ستلعب المكثفة دور قاطعة مغلقة لا مقاومة لها (كونها مثالية)، وبالتالي فإن الفلطية بين طرفيها ستكون معدومة، وبالتالي فإن نسبة فلطية الخرج إلى فلطية الدخل هي الصفر.
لهذه الأسباب تسمى الدارة السابقة مرشح تمرير منخفض Low-Pass Filter لأنها تسمح بمرور التيار فقط من أجل التواترات المنخفضة. نسمي الترددتردد القطع، وهو تردد مميز للدارة.
ثانيا: طور تابع نقل الدارة RC
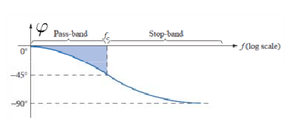
يعطى الطور بالعلاقة:
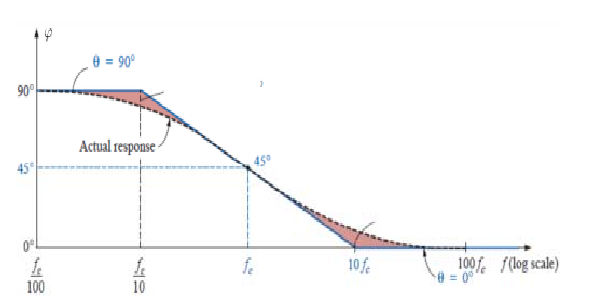
من الشكل نلاحظ أن الطور سالب دوما، وهذا يعني أن إشارة الخرج متأخرة دوما عن إشارة الدخل، ويزداد هذا التأخر بازدياد التردد المطبق على الدارة.
الآن وقد استعرضنا كلا من طويلة وطور تابع النقل فإننا سنتحدث الآن عن تمثيل بود.
تمثيل بود
يُعبر عن طويلة وطور تابع نقل دارة ما بدلالة التردد بالاستجابة الترددية للدارة. يقوم تمثيل بود بتسهيل المقارنة بين الاستجابة الترددية لدارات مختلفة، ومن أجل مجال واسع من الترددات.
ما يميز منحني بود لطويلة طور تابع النقل أي Hdb هو أن المحور الشاقولي بدلا من أن يمثل أو فإنه يقوم بتمثيل اللوغاريتم العشري لهما، أي: أو . أما المحور الشاقولي فإنه يقوم بتمثيل قيمة الديسيبل للطويلة، أي اللوغاريتم العشري لها مضروبة بالقيمة 20:
مخطط بود في الحقيقة هو مخطط لوغاريتمي. لذلك سنتناول بعض المعلومات السريعة عن المخططات اللوغاريتمية قبل متابعة الحديث عن مخطط بود.
المخطط اللوغاريتمي
هو، كما أشرنا من قبل، المخطط الذي يشير فيه المحور الشاقولي إلى لوغاريتم القيمة بدلا من القيمة ذاتها. ليكن لدينا محورا لمخطط خطي تقليدي يمثل مدى زمني لألف سنة. 0 100 200 300 400 500 600 700 800 900 1000 |_____|_____|_____|_____|_____|_____|_____|_____|_____|_____| لو اعتمدنا المخطط اللوغاريتمي لأصبح المحور على الشكل التالي: 1 10 100 1000 |_____________|_____________|______________| 100 101 102 103 ستكون تقسيمات المخطط اللوغاريتمي قوى العدد عشرة (في حال اللوغاريتم العشري)، أي الصفر والواحد والاثنان والثلاثة، هذا سيتيح تمثيلا لعدد أكبر من السنين بتقسيمات أقل. وبالتأكيد فإن أمورا عدة سوف تتغير.
الشيء الأول الذي سيتغير هو مواضع التقسيمات، فمن أجل معرفة موضع الرقم 2 علينا أن نقوم بحساب log10 20 فسنجد أنها تقريبا 0.3 أما بالنسبة للرقم 4 فسنجد أن قيمة اللوغاريتم هي 0.6. فالقيم كلها تتقارب نحو العشرة على النحو المشار إليه في المخطط أدناه.
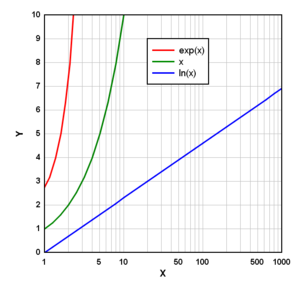
الشيء الأخير الذي يجب أن نشير إليه هو أن شكل المخططات البيانية للتوابع المألوفة لدينا سيكون مختلفا أيضا. وهذا أمر بدهي. فالخط المستقيم في مخطط لوغاريتمي هو الخط البياني لتابع . فكل نقطة من المحور الأفقي ولتكن x، يقابلها قيمة اللوغاريتم لها على المحور الشاقولي. لكن بما أن النقطة x هي في الحقيقة ، فأصبحت كل قيمة من المحور الأفقي تقابل نفسها على المحور الشاقولي. يبين الشكل مخططات لبعض التوابع المألوفة.
أما الآن، وقد تحدثنا عن كل من المخططات اللوغاريتيمية وطويلة تابع النقل وطوره، فسننتقل للحديث عن مخطط بود لتابع النقل.
مخطط بود لطويلة تابع النقل
لقد كان تابع النقل في دارة RC التي تعاملنا معها:
وقمنا بحساب طويلة تابع النقل فوجدناها:
الآن من أجل إيجاد مخطط بود، علينا أولا أن نحسب طويلة تابع النقل H بالديسيبيل، فنجد:
وبالتالي:
سنقوم باستعراض طريقة لرسم هذا المخطط بشكل تقريبي. حيث سندرس المخطط Hdb من أجل الترددات العالية والترددات المنخفضة.
عند الترددات المنخفضة أي من أجل قيم يمكننا إهمال فيكونHdb بالشكل الآتي:
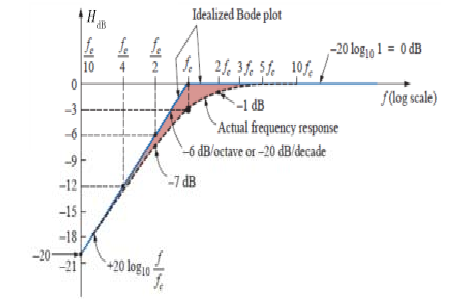
لذلك نرسم خطا مستقيما Hdb = 0 من 0 وحتى .
عند الترددات المرتفعة أي من أجل قيم يصبح الحد كبيرا بحيث يمكن إهمال الواحد فيمكن عندئذ كتابةHdb بالشكل الآتي:
وبالتالي لدينا الخط البياني:
في الحقيقة هذه المعادلة هي معادلة مستقيم مائل. لاحظ أنه يمكنك أن تنظر إلى أن تقابل x في معادلة المستقيم ، وبالتالي فإننا نرسم Hdb كمستقيم ميله . الواحدة هنا هي ديسيبيل/ديكيد، والمقصود بالديكيد decade تقسيمة المخطط اللوغاريتيمي أي المسافة بين و ، فهذا يعني أنه لو ازداد التردد بعشرة أضعاف، فإن التغير في مخطط Hdb سيكون .
للتحقق من ذلك، نقوم بالتعويض في المعادلة بـ فنجد:
من أجل رسم المستقيم، نعوّضHdb = 0 في معادلة المستقيم فنجد أن وبالتالي فإن . فالمستقيم يقطع المحور الأفقي في النقطة .
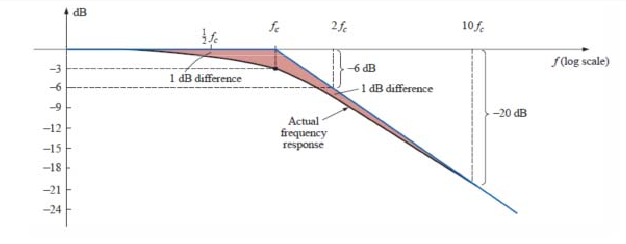
لدى مقارنة المستقيمين اللذين قمنا برسمهما مع مخطط بود الفعلي للدارة Hdb فإنناسنلاحظ أنهما مقارباه. وغالبا ما تستخدم المقاربات بدل التمثيل الحقيقي لمخططات بود.
أشرنا سابقا إلى الميل ذو الواحدة ديسيبيل/ديكيد، والذي يعبر عن مقدار التغير في Hdb عند تغير التردد إلى عشرة أضعافه. لو حاولنا تتبع تغير Hdb عند تغير التردد إلى ضعفه فقط، فإن هذا الميل يقدر بواحدة تسمى ديسيبيل/أوكتاف. ففي مثالنا هذا يمكننا الحصول عليها من خلال التعويض، فنجد:
دراسة خرج الدارة عند المقاومة
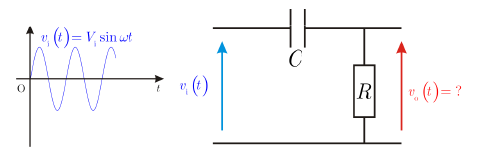سنقوم الآن بدراسة مشابهة لإشارة الخرج الملتقطة بين طرفي المقاومة R.
بتطبيق قانون مجزئ الفلطية، نجد أن
وبالتالي يكون تابع النقل للدارة:
فتكون الطويلة: ويكون الطور:
الآن يمكننا أن نكتب تابع النقل بالديسيبيل:
عند الترددات المنخفضة يمكننا إهمال 1 أمامفيكون Hdb بالشكل الآتي:
أي
إذا لدينا مستقيم ميله يقطع المحور الأفقي في النقطة .
عند الترددات المرتفعة نلاحظ أنه يمكننا إهمال النسبة أمام الواحد، فيمكن عندئذ كتابةHdb بالشكل الآتي:
ندعو هذه الدارة مرشح تمرير عالي. وها هو تمثيل بود للدارة.
ومن أجل رسم طور تابع النقل، نلاحظ أن من أجل الترددات المنخفضة، ومن أجل الترددات العالية، لذلك يتم تمثيل التابع وفق الشكل التالي:
بعد استعراض هذين المثالين، أصبح في مقدورك الحصول على تمثيل بود لأي دارة، بمجرد معرفة تابع النقل لها. وهذه بعض النماذج نتركك لتتحقق من صحتها بنفسك!
المرشح الكهربائي المطاوع
هو عبارة عن دارة كهربائية مكونة من عناصر كهربائية مطاوعة فقط (لا تولد الطاقة)، مصممة لتمرير إشارة معينة مرغوبة من بين خليط من الإشارات المرغوبة وغير المرغوبة.
تستخدم كثيرا في مجال الاتصالات حيث غالبا ما نرغب باستقبال أنواع محددة من الإشارات، لذلك يتم تصميم دارات تقوم بتمرير إشارات ترددات ذات تواتر معين، وترفض التواترات الأخرى، قد تكون دارات معقدة كما في التلفاز والمذياع والهاتف النقال، أو دارات بسيطة مثل دارة RC التي استعرضناها في المحاضرة السابقة. لهذا السبب فإن أجهزة الراديو العادية لا تستطيع أن تستقبل إشارات الراديو التي تستخدمها الشرطة.
هذه مخطط لطويلة تابع النقل لمرشح تمرير منخفض، فهو يقوم بتمرير الإشارات ذات التواتر المنخفض فقط.
بينما يقوم مرشح التمرير العالي بتمرير الإشارات ذات التواتر العالي فقط.
هنا يقوم مرشح تمرير حزمة بتمرير الإشارات التي ينتمي تواترها إلى مجال معين بينما يستبعد سائر الحزمة الأخرى.
أما مرشح رفض حزمة يقوم يمنع الإشارات التي ينتمي تواترها إلى مجال معين من المرور بينما يسمح لسائر الإشارات الأخرى.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
دراسة استجابة RC واقعية
في المحاضرة السابقة قمنا بدراسة استجابة دارة RC مثالية، حيث لا توجد مقاومة للمكثفة. الآن سندرس استجابة المقاومة في حال وجود مكثفة لها مقاومة. وهذا يكافئ وجود مقاومة موصولة على التسلسل مع المكثفة.
نعلم أن استجابة الدارة من الشكل: أو عقديا:
بتطبيق مجزئ الفلطية نجد أن فرق الكمون بين طرفي المقاومة هو:
وبالتالي وإذا فرضنا أن فسيكون تابع النقل على الشكل الآتي:
الآن نستطيع أن نحصل على كل من طويلة تابع النقل وطوره:
و
إذا سيكون Hdb على الشكل الآتي:
لو رجعنا إلى Hdb لدارة RC المثالية في المحاضرة المادية، لوجدنا أن الفرق هو وجود الحد الإضافي الذي لا يتعلق بالنبض فهو مقدار ثابت، وبالتالي فإن مخطط بود الجديد سينتج عن القديم بانسحاب على المحور الشاقولي.
بما أن المقدار مقدار أصغر من الواحد، فإن لوغاريتم هذا المقدار سيكون سالبا، وبالتالي فإن انسحاب مخطط بود سيكون نحو الأسفل.
وهذا هو المخطط الجديد الذي ينتج عن مجموع الحدين المشكلين لـ Hdb :
