ضياء
في الفلك، الضياء أو اللمعان Luminosity هو مقدار الطاقة الإشعاعية (Radiant Energy) التي يُطلقها جسم ما (النجوم خصوصا) في الثانية الواحدة. تُقاس الطاقة الإشعاعية للنجوم بطريقتين: الظاهرية (وهي حساب الطاقة المرئية فقط وتقاس بالقدر الظاهري) و البولومترية (وهي حساب الطاقة الحقيقية للنجم وهي "السطوع" يتم تحديدها من خلال حساب كل الإشعاع الصادر من النجم بكل الأطياف ويتم ذلك من خلال حساب حرارة النجم). حيث أن الطريقة الأولى تقيس طاقة النجم التي تصل إلى الأرض بينما الثانية تُقاس بناء على بعد ثابت من النجم وهو 10 فراسخ فلكية. يتم قياس السطوع بوحدة الواط ولكن عادة ما يستخدم سطوع الشمس كمقياس لتسهيل حسابه ويُكتب: . ويبلغ سطوع الشمس 3.846×1026 واط وأيضا كثيرا ما يستخدم القدر المطلق كوحدة لقياسه.
إن السطوع هو مقياس مطلق للنجم ليس له علاقة بالمسافة أو بعده عنا، وبالتالي سواء حُسب من خلال القدر المطلق للأشعة المرئية أو كامل الإشعاع والحرارة للنجم يجب أن توحد المسافة لكل النجوم وكأنها مصطفة على نفس البعد من الأرض. والقدر الظاهري هو لمعان النجم كما هو مشاهد من الأرض والذي يختلف حسب بعد النجم.
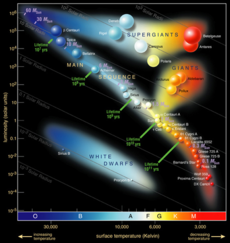
يعتمد مقدار سطوع النجم على كثافته. وقد قسم الفلكيون سطوع النجوم إلى خمسة أقدار يُرمز لها بالأرقام الرومانية. وكلما ازداد الرقم أصبح اللمعان أقل، حيث أن النجوم من القدر "V" (بالأرقام الحديثة "5") هي أقل النجوم سطوعا. وهناك قدر سادس أخير حيث إن القدر "I" (بالأرقام الحديثة "1") ينقسم إلى قدرين.
أصناف السطوع النجمي الصنف، الوصف / مثال
Ia، نجم فوق العملاق / منكب الجوزاء، رجل الجبار.
Ib، نجوم فوق العملاقة عاتمة / نجم الجدي.
II، نجوم عملاقة ساطعة / مينتاكا (نجم في حزام كوكبة الجبار).
III، نجوم عملاقة اعتيادية / السماك الرامح.
IV، نجوم دون العملاقة / آخر النهر (نجم جنوبي ساطع).
V، التسلسل الرئيسي / الشمس، الشعرى اليمانية.
قياس الضياء
 مقالة مفصلة: استضواء
مقالة مفصلة: استضواء
في القياس الضوئي، يستخدم الضياء خطأ في بعض الأحيان للدلالة على الاستضواء وهو كثافة شدة الإضاءة في اتجاه محدد. وحدة الاستضواء في نظام الوحدات الدولي هي قنديلة في المتر المربع.
 مقالة مفصلة: الفضاء اللوني ص ش ض
مقالة مفصلة: الفضاء اللوني ص ش ض
قد يشار أحيانا خطأ إلى ض في الفضاء اللوني ص ش ض على أنه الضياء. وتحسب ض في هذه الحالة 1/2 (MAX + MIN) حيث MAX و MIN هي أعلى وأخفض قيم لمكونات ح خ ز عند تحويلها إلى الفضاء اللوني ص ش ض.
 مقالة مفصلة: دالة الضياء
مقالة مفصلة: دالة الضياء
دالة الضياء إنگليزية: luminosity function أو دالة التألق[1] أو الدالة الضيائية[1] وتعرف أيضا بتابع الفعالية الضوئية يصف متوسط الحساسية البصرية للعين البشرية للضوء عند الأطوال الموجية المختلفة. وهناك دالتان للضياء تستخدمان عادة. عند مستويات الإضاءة اليومية، دالة الضياء للرؤية النهارية تقارب بطريقة أفضل استجابة العين البشرية. وعند مستويات الإضاءة المنخفضة، تتغير استجابة العين البشرية، ويمكن استخدام منحني الرؤية الغلسية.
القدر
| التجميع | النطاق | مثال | VMag |
|---|---|---|---|
| أول قدر | < 1.5 | Vega | 0.03 |
| ثاني قدر | 1.5 to 2.5 | Denebola | 2.14 |
| ثالث قدر | 2.5 to 3.5 | Rastaban | 2.79 |
| رابع قدر | 3.5 to 4.5 | Sadalpheretz | 3.96 |
| خامس قدر | 4.5 to 5.5 | Pleione | 5.05 |
| سادس قدر | 5.5 to 6.5 | 54 Piscium | 5.88 |
| سابع قدر | 6.5 to 7.5 | HD 40307 | 7.17 |
| ثامن قدر | 7.5 to 8.5 | HD 113766 | 7.56 |
| تاسع قدر | 8.5 to 9.5 | HD 149382 | 8.94 |
| عاشر قدر | 9.5 to 10.5 | HIP 13044 | 9.98 |

صيغة الضياء
معادلة شتفان-بولتسمان applied to a black body gives the value for luminosity for a black body, an idealized object which is perfectly opaque and non-reflecting:[3]
- ,
حيث A هي المساحة، T هي درجة الحرارة (بالكلڤن) و σ هي ثابت شتفان-بولتسمان، بقيمة 5.670373(21)×10−8 W m−2 K−4.[4]
Imagine a point source of light of luminosity that radiates equally in all directions. A hollow sphere centered on the point would have its entire interior surface illuminated. As the radius increases, the surface area will also increase, and the constant luminosity has more surface area to illuminate, leading to a decrease in observed brightness.
- ,
حيث
- is the area of the illuminated surface.
- is the flux density of the illuminated surface.
The surface area of a sphere with radius r is , so for stars and other point sources of light:
- ,
where is the distance from the observer to the light source.
It has been shown that the luminosity of a star (assuming the star is a black body, which is a good approximation) is also related to temperature and radius of the star by the equation:[3]
- ,
where
- σ is the Stefan–Boltzmann constant 5.67×10−8 W·m−2·K−4.
Dividing by the luminosity of the Sun and cancelling constants, we obtain the relationship:[3]
- ,
where and are the radius and temperature of the Sun, respectively.
For stars on the main sequence, luminosity is also related to mass:
- .
صيغ القدر
الظاهر
The magnitude of a star is a logarithmic scale of observed visible brightness. The apparent magnitude is the observed visible brightness from Earth, and the absolute magnitude is the apparent magnitude at a distance of 10 parsecs. Given a visible luminosity (not total luminosity), one can calculate the apparent magnitude of a star from a given distance (ignoring extinction):
حيث
- is the apparent magnitude of the star (a pure number)
- is the apparent magnitude of the Sun (also a pure number)
- is the visible luminosity of the star
- is the solar visible luminosity
- is the distance to the star
- is the distance to the Sun
Or simplified, given , :
- , where is measured in .
Bolometric
The difference in bolometric magnitude is related to the luminosity ratio according to:
which makes by inversion:
حيث
- is the Sun's (sol) luminosity (bolometric luminosity)
- is the star's luminosity (bolometric luminosity)
- is the bolometric magnitude of the Sun
- is the bolometric magnitude of the star.
تحديات حاسوبية
An example of two distinct debated scenarios are:
| Parameter | Scenario I | Scenario II |
|---|---|---|
| Angular Diameter | Bester 1996: 56.6 ± 1.0 mas [5] | Perrin 2004: 43.33 ± 0.04 mas [6] |
| Distance | Harper 2008: 197 ± 45 pc [7] | van Leeuwen 2007: 152 ± 20 pc [8] |
| Temperature | Smith 2009: 3,300 K [5] | Perrin 2004: 3,641 K [6] |
To determine the star's luminosity, there are 3 computational steps:
- 1) convert the star's angular diameter in arcseconds into its radius in astronomical units (AU);
- 2) convert the star's radius in AU into its solar radius ; and finally
- 3) convert its solar radius and temperature (kelvin) into solar luminosity.
Arcseconds to AU
The calculations begin with the formula for a star's angular diameter, as follows:
حيث
represents Betelgeuse's angular diameter in arcseconds,
the Distance from Earth in parsecs
Betelgeuse's diameter in AU, and
Betelgeuse's Radius in AU. Therefore:
- (rounded)
- (rounded)
الوحدة الفلكية إلى R☉
To convert the above into solar units, the math is straightforward. Since 1 AU = 149,597,871 km and the mean diameter of the Sun = 1,392,000 km (hence a mean radius of 696,000 km), the calculation is as follows:
R☉ إلى L☉
Incorporating the R☉ results into the luminosity formula outlined earlier where B = Betelgeuse, L = Luminosity, R = Radius and T = Temperature, we can calculate Betelgeuse's luminosity per each scenario, as follows:
These luminosity calculations do not take into consideration error factors relating to angular diameter or distance measurements nor any diminution caused by extinction, which in the case of Betelgeuse has been estimated at around 3.1%. Also, while the calculations are correct and useful, in practice they are often performed in reverse because the distance to most stars[بحاجة لمصدر], and hence their size, cannot be determined directly while quantities such as the luminosity and temperature can be estimated from other observable quantities.[بحاجة لمصدر]
الهامش
- ^ أ ب وفقا لمعجم المصطلحات العلمية والفنية والهندسية الجديد
- ^ "COROT discovers its first exoplanet and catches scientists by surprise". وكالة الفضاء الأوروپية. 3 May 2007. Retrieved 2 July 2012.
- ^ أ ب ت خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةAUSTRALIA2004 - ^ "CODATA Value: Stefan-Boltzmann constant". The NIST Reference on Constants, Units, and Uncertainty. US National Institute of Standards and Technology. June 2011. Retrieved 2013-11-03.
{{cite web}}: External link in|work= - ^ أ ب خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةSMITH2009 - ^ أ ب خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةPERRIN2004 - ^ خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةHARPER2008 - ^ خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةVANLEEUWEN2007
للاستزادة
- Böhm-Vitense, Erika (1989). "Chapter 6. The luminosities of the stars". Introduction to Stellar Astrophysics: Volume 1, Basic Stellar Observations and Data. Cambridge University Press. pp. 41–48. ISBN 978-0-521-34869-0.
{{cite book}}: External link in|chapterurl=|chapterurl=ignored (|chapter-url=suggested) (help)

















![{\displaystyle m_{\rm {star}}=m_{\odot }-2.5\log _{10}\left[{\frac {L_{\rm {star}}}{L_{\odot }}}\left({\frac {d_{\odot }}{d_{\rm {star}}}}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa13db5bce810b9d7667302abaefae0e83742cab)






















