الدارات الخطية من المرتبة الأولى

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 تعريف

الدارة الخطية من الدرجة الأولى: هي الدارة التي تحكمها معادلة تفاضلية من الدرجة الأولى من الشكل:

حيث كل من و ثوابت، و تابع للفلطية أو التيار بالنسبة للزمن.

الأمجد توفيق اصطيف ساهم بشكل رئيسي في تحرير هذا المقال

يمكن تمثيل كل دارة خطية ثنائية القطب من الدرجة الأولى بثنائي قطب مكافئ مكون من عنصرين أساسيين: مقاومة ووشيعة، أو مقاومة ومكثفة، مربوطتين على التسلسل والتفرع. سنقوم في هذا الفصل بدراسة التراكيب المختلفة لهذه الدارات، عند تطبيق نوعين مختلفين من الإشارة: الإشارة الخطوية والإشارة الجيبية.

 تابع الخطوة

ملف:Unitfunction.png يعطى تابع الخطوة بالعلاقة أدناه، حيث يعطي قيمة ثابتة E من أجل t > 0 وقيمة معدومة من أجل t < 0.

 أولا: دارة RC تسلسلية

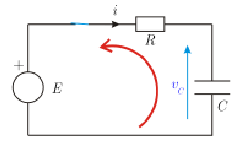
 دارة الشحن

لتكن لدينا الدارة المبينة في الشكل. نقوم بإغلاق القاطعة عن t = 0، نفرض أن المكثفة غير مشحونة في البداية، وبالتالي تكون القيمة الابتدائية للفلطية على طرفي المكثفة معدومة . نقوم بتطبيق قانون كرشوف للفلطية فنجد:

ونعلم أن التيار في الدارة يعطى بالعلاقة: ،نعوض في معادلة كرشوف فنحصل على المعادلة التفاضلية: وحلها (حاول أن تتحقق منه!) هو:

A هو ثابت المكاملة الكيفي، نقوم باستخدام القيمة الابتدائية ونعوّضها في المعادلة السابقة فنجد أن وبالتالي تصبح معادلة الفلطية: .

وبالتالي يمكننا الحصول على معادلة التيار:

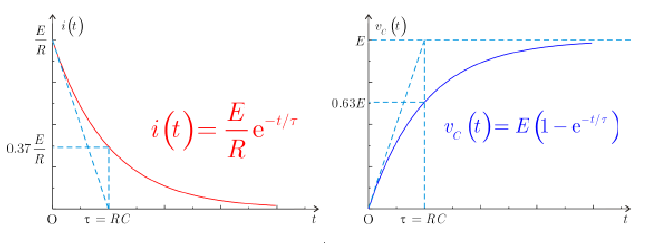
نقوم برسم المخطط البياني لكل من الفلطية والتيار بالنسبة للزمن. لاحظ كيف تتزايد قيمة الفلطية بين طرفي المكثفة من الصفر لتبلغ نظريا القيمة العظمى لها E في اللانهاية. أما بالنسبة للتيار، فهو يأخذ قيمة عظمى في البداية E/R ثم تتناقص مع مرور الزمن لتبلغ الصفر في اللانهاية.

لنحاول إيجاد معادلة المماس لمنحني الفلطية في اللحظة 0. نحصل على الميل من معادلة المشتق، وهو التيار، فنجد أن المماس يقطع المقارب E في النقطة .

عندما نكون في اللحظة الزمنية نلاحظ أن الفلطية تصبح: . يرمز لهذا الزمن والذي تشحن فيه 63% من المكثفة على النحو التالي: ، ويسمى الثابت الزمني للدارة.

يمكننا أن نلاحظ أيضا أنه ومن أجل زمن ، تصبح الفلطية: . فالمقدار مقدار مميز للدارة RC ويستخدم في العديد من التطبيقات.

تعطى شحنة المكثفة بالعلاقة: ، فبعد زمن ستصل شحنة المكثفة إلى 99% بالمئة من قيمتها النهائية.

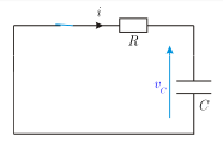
 دارة التفريغ

في هذه الدارة نقوم بقصر منبع الفلطية، لتتكون الدارة المبينة بالشكل، وبتطبيق قانون كرشوف للفلطية نحصل على المعادلة التفاضلية:

وحلها: ، وبما أن القيمة الابتدائية للفلطية بين طرفي المكثفة المشحونة هي E فتكون معادلة الفلطية: .

وكما فعلنا في دارة الشحن نحصل على عبارة التيار من خلال العلاقة:

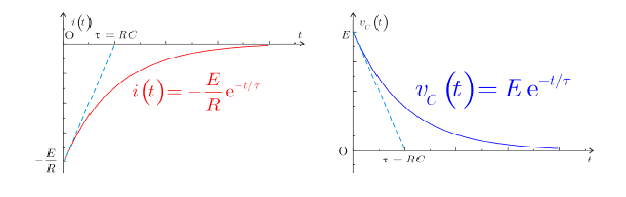
نقوم من جديد بدراسة التمثيل البياني لكل من التابعين.

لاحظ كيف تتغير قيمة التيار فجأة من E/R- إلى الصفر، وكيف تتناقص شحنة المكثفة من E حتى الصفر. المماس للمنحني من أجل الزمن t = 0 يقطع محور الزمن عند .

فبعد فترة زمنية طويلة، ستكون القيمة النهائية لكل من التيار والفلطية صفرا، وبالتالي لن يمر أي تيار كهربائي في الدارة.

 الإشارة المستطيلة

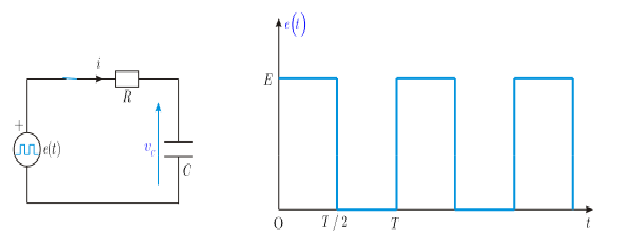خلال دور واحد T، يعطي منبع الفلطية ذو الإشارة المستطيلة فلطية ثابتة E خلال نصف دور، وفلطية معدومة في نصف الدور الآخر. سنستخدم هذا المنبع بدل المنبع الذي يقدم إشارة خطوية في دارة RC السابقة، وندرس تأثير ذلك على استجابة الدارة، وعلى التيار المار فيها. لهذا الغرض سنقوم برسم الخطين البيانيين لكل من الإشارة المطبقة والتيار المار في الدارة.

عندما يكون دور الإشارة المستطيلة T أكبر بكثير من الثابت الزمني للدارة، ستُشحن المكثفة في نصف دور وتفرّغ في نصف الدور الآخر بسرعة كبيرة. لهذا السبب نلاحظ من الخط البياني أن التيار يتناقص بحدة من E/R إلى الصفر في نصف الدور الأول (دور الشحن)، ليعود بعد ذلك ويتناقص بحدة أيضا من E/R إلى الصفر (ولكنه يأخذ جهة معاكسة لجهة الشحن، لهذا تكون قيمته المطلقة سالبة).

أما عندما يكون دور الإشارة المستطيلة T أصغر بكثير من الثابت الزمني للدارة، فما إن يبدأ التيار بالمرور وتبدأ المكثفة بشحن نفسها حتى تنعدم الفلطية التي يقدمها المنبع، فلا تصل شحنة المكثفة (نسبة إلى شحنتها الكلية) إلا إلى نسبة ضئيلة. هذا يشبه إلى حد بعيد قيامك بتشغيل وإطفاء التلفاز بشكل متكرر وسريع. لهذا السبب نلاحظ أن قيمة التيار تتناقص ببطء وأنها لا تصل أبدا إلى الصفر.

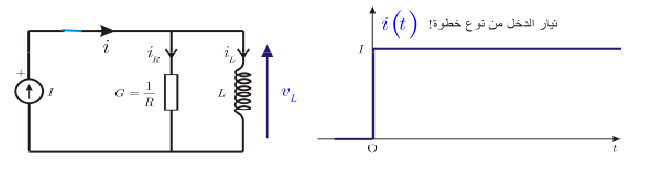
 ثانيا: دارة RL تسلسلية:

لتكن لدينا الدارة المبينة بالشكل. تيار الدخل خطوي، يأخذ قيمة ثابتة I من أجل زمن

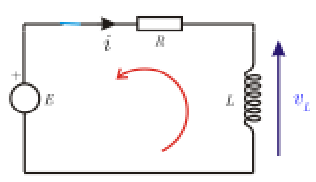
سنقوم بتحويل منبع التيار إلى فلطية، وسندرس الدارة بشكل مشابه لما قمنا به سابقا. وسنفترض أن الدارة في حالة راحة، أي أن التيار معدوم في الوشيعة لحظة تطبيق التيار t = 0.

بتطبيق قانون كرشوف للفلطية نجد:

ونعلم أن فلطية الوشيعة تعطى بالعلاقة:

نعوض في المعادلة السابقة فنحصل على المعادلة التفاضلية التالية:، وهي بالطبع معادلة تفاضلية من الدرجة الأولى. حلها هو: ، حيث A ثابت المكاملة يتعلق بالشروط الابتدائية. وسنجد أنه من أجل فسيكون . بالطبع يمكننا الحصول على فلطية الوشيعة من خلال الاشتقاق، فنجد:

. يسمى المقدار الثابت الزمني للدارة.

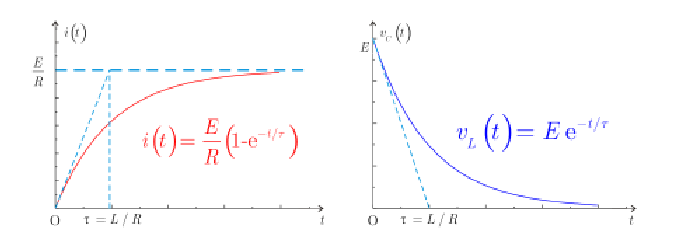
لنلق الآن نظرة على المخططين البيانيين لكل من تيار الوشيعة وفلطيتها. نلاحظ أن مماس منحني التيار يقطع المقارب في اللحظة الزمنية الموافقة للثابت الزمني للدارة، ونلاحظ أيضا أن :

أما بالنسبة لمنحني الفلطية فنجد أن المماس عند t = 0 يقطع محور السينات عند الثابت الزمني للدارة، كما نلاحظ أن:

لهذا السبب فإن الدارة تصل إلى الحالة النهائية بعد زمن بتقريب جيّد

أما من أجل فستكون قيمة التيار:

 سلوك الدارات في النمط الجيبي

لقد أشرنا في الفصل السابق إلى إمكانية تمثيل المقادير الجيبية باستخدام الأعداد العقدية. لهذا الأمر أهمية كبيرة، إذ إن تطبيق قوانين كرشوف على التمثيل العقدي لكل من التيار والفلطية والممانعات سيعطي نتائج صحيحة.

بالإضافة إلى اعتماد هذا المبدأ في دراسة سلوك الدارات في النمط الجيبي، علينا أن نتذكر ميزة هامة للنمط الجيبي، وهي أن كل التوابع الزمنية الجيبية للتيارات والفلطيات في الدارة لها نبض المنبع المحرض نفسه، وهذا يسمح بتبسيط حل معادلات الدارات.

قبل أن ندرس نموذجا في كيفية دراسة استجابة دارة في نمط جيبي (في المحاضرة القادمة إن شاء الله)، سنقوم باستعراض لكيفية تمثيل ممانعات دارات مختلفة.

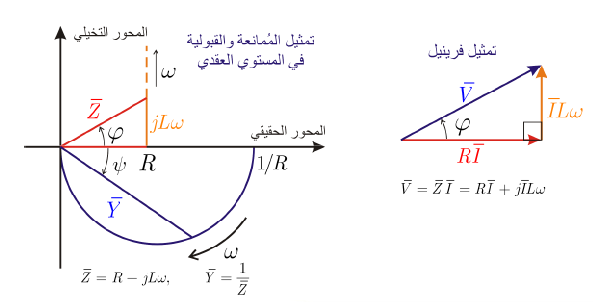
 دارة RC تسلسلية

تعطى الممانعة العقدية للدارة بالعلاقة:

وبما أنها مقدار عقدي فيمكن كتابتها بالشكل:

يمكن حساب طويلة وطور الممانعة من خلال علاقات التحويل إلى المطاور (التي تحدثنا المحاضرة الماضية) فنجد:

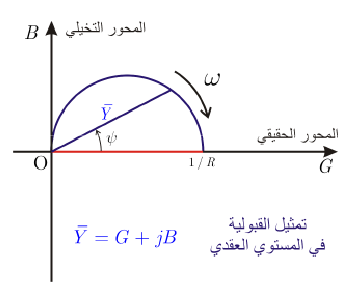
قبولية الدارة هي مقلوب الممانعة، وتعطى بالعلاقة:

نلاحظ أن الجزء الحقيقي من الممانعة ثابت لا يتعلق بالنبض المطبق ، أما الجزء التخيلي فهو يسعى نحو الصفر من أجل قيم كبيرة له، ويسعى نحو اللانهاية من أجل قيم صغيرة للنبض.

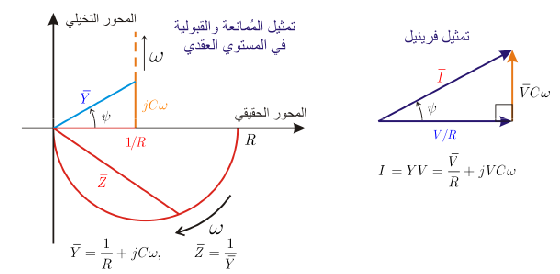
التمثيل البياني يمكننا تمثيل الممانعة الكلية هي حصيلة جمع ممانعة المقاومة الحقيقية تماما إلى ممانعة المكثفة التخيلية تماما، وستأخذ الشكل المبين في المخطط البياني.

لو قمنا بضرب كل من الأشعة في المخطط بالتيار العقدي، فسنحصل على ما يسمى بتمثيل فرينيل، وهكذا سيمثل شعاع كل ممانعة شعاع الفلطية المار بتلك الممانعة،

من أجل تمثيل القبولية، سنعتمد طريقة هندسية لتمثيل مقلوب عدد عقدي بيانيا. نعلم بداية أن زاوية مقلوب عدد عقدي تساوي زاوية العدد بالقيمة المطلقة وتعاكسه بالإشارة، لذلك يمكن تمثيل ذلك بيانيا بسهولة. أما بالنسبة للطويلة فيمكن البرهان على أن النقطة الممثلة لمقلوب عدد عقدي تقع على الدائرة التي قطرها هو مقلوب الجزء الحقيقي والمارة من مركز الإحداثيات. لذلك ستكون القبولية في دارتنا:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

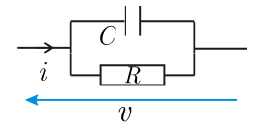
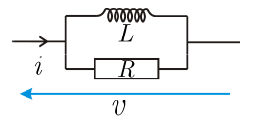
 دارة RC تفرعية

تعطى القبولية العقدية للدارة بالعلاقة:

حيث: ،

نلاحظ أن الجزء الحقيقي من القبولية ثابت لا يتعلق بالنبض المطبق ، أما الجزء التخيلي فهو يسعى نحو الصفر من أجل قيم صغيرة له، ويسعى نحو اللانهاية من أجل قيم كبيرة للنبض.

وهذا هو التمثيل البياني للمانعة والقبولية:

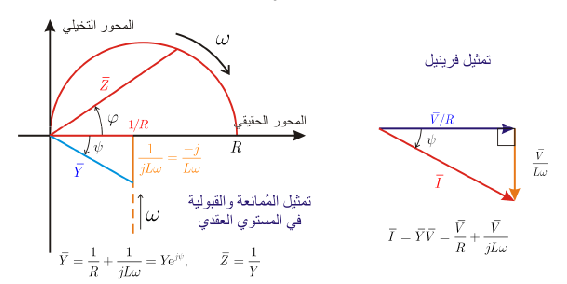
 دارة RL تفرعية

تعطى القبولية العقدية للدارة بالعلاقة:

حيث: ،

نلاحظ أن الجزء الحقيقي من القبولية ثابت لا يتعلق بالنبض المطبق ، أما الجزء التخيلي فهو يسعى نحو الصفر من أجل قيم كبيرة للنبض، ويسعى نحو اللانهاية من أجل القيم الصغيرة.

ويمثل الشكل أدناه التمثيل البياني لكل من الممانعة والقبولية:

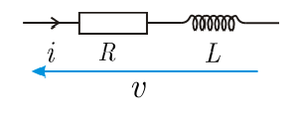
 دارة RL تسلسلية

تعطى الممانعة العقدية للدارة بالعلاقة:

حيث:

، قبولية الدارة هي مقلوب الممانعة، وتعطى بالعلاقة:

نلاحظ أن الجزء الحقيقي من الممانعة ثابت لا يتعلق بالنبض المطبق ، أما الجزء التخيلي فهو يسعى نحو الصفر من أجل قيم صغيرة للنبض، ويسعى نحو اللانهاية من أجل القيم الكبيرة.

التمثيل البياني