التفاف (رياضيات) Involution (mathematics)
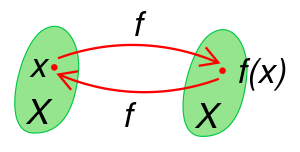
في الرياضيات، an involution, involutory function, or self-inverse function[1] is a function f that is its own inverse,
- f(f(x)) = x
for all x in the domain of f.[2] Equivalently, applying f twice produces the original value.
السمات العامة
Any involution is a bijection.
The identity map is a trivial example of an involution. Examples of nontrivial involutions include negation (x ↦ −x), reciprocation (x ↦ 1/x), and complex conjugation (z ↦ z) in arithmetic; reflection, half-turn rotation, and circle inversion in geometry; complementation in set theory; and reciprocal ciphers such as the ROT13 transformation and the Beaufort polyalphabetic cipher.
The composition g ∘ f of two involutions f and g is an involution if and only if they commute: g ∘ f = f ∘ g.[3]
التفافات في فئات محدودة
The number of involutions, including the identity involution, on a set with n = 0, 1, 2, ... elements is given by a recurrence relation found by Heinrich August Rothe in 1800:
- and for
The first few terms of this sequence are 1, 1, 2, 4, 10, 26, 76, 232 (المتتالية A000085 في OEIS); these numbers are called the telephone numbers, and they also count the number of Young tableaux with a given number of cells.[4] The number an can also be expressed by non-recursive formulas, such as the sum
The number of fixed points of an involution on a finite set and its number of elements have the same parity. Thus the number of fixed points of all the involutions on a given finite set have the same parity. In particular, every involution on an odd number of elements has at least one fixed point. This can be used to prove Fermat's two squares theorem.[5]
الالتفاف في مختلف مجالات الرياضيات
الدوال ذات القيم الحقيقية
The graph of an involution (on the real numbers) is symmetric across the line y = x. This is due to the fact that the inverse of any general function will be its reflection over the line y = x. This can be seen by "swapping" x with y. If, in particular, the function is an involution, then its graph is its own reflection.
Some basic examples of involutions include the functions
Besides, we can construct an involution by wrapping an involution g in a bijection h and its inverse (
). For instance :
الهندسة الإقليدية
A simple example of an involution of the three-dimensional Euclidean space is reflection through a plane. Performing a reflection twice brings a point back to its original coordinates.
Another involution is reflection through the origin; not a reflection in the above sense, and so, a distinct example.
These transformations are examples of affine involutions.
الهندسة الإسقاطية
An involution is a projectivity of period 2, that is, a projectivity that interchanges pairs of points.[6]
- Any projectivity that interchanges two points is an involution.
- The three pairs of opposite sides of a complete quadrangle meet any line (not through a vertex) in three pairs of an involution. This theorem has been called Desargues's Involution Theorem.[7] Its origins can be seen in Lemma IV of the lemmas to the Porisms of Euclid in Volume VII of the Collection of Pappus of Alexandria.[8]
- If an involution has one fixed point, it has another, and consists of the correspondence between harmonic conjugates with respect to these two points. In this instance the involution is termed "hyperbolic", while if there are no fixed points it is "elliptic". In the context of projectivities, fixed points are called double points.[6]
Another type of involution occurring in projective geometry is a polarity that is a correlation of period 2.[9]
الجبر الخطي
In linear algebra, an involution is a linear operator T on a vector space, such that قالب:Itco2 = I. Except for in characteristic 2, such operators are diagonalizable for a given basis with just 1s and −1s on the diagonal of the corresponding matrix. If the operator is orthogonal (an orthogonal involution), it is orthonormally diagonalizable.
For example, suppose that a basis for a vector space V is chosen, and that e1 and e2 are basis elements. There exists a linear transformation f that sends e1 to e2, and sends e2 to e1, and that is the identity on all other basis vectors. It can be checked that f(f(x)) = x for all x in V. That is, f is an involution of V.
For a specific basis, any linear operator can be represented by a matrix T. Every matrix has a transpose, obtained by swapping rows for columns. This transposition is an involution on the set of matrices. Since elementwise complex conjugation is an independent involution, the conjugate transpose or Hermitian adjoint is also an involution.
The definition of involution extends readily to modules. Given a module M over a ring R, an R endomorphism f of M is called an involution if قالب:Itco2 is the identity homomorphism on M.
Involutions are related to idempotents; if 2 is invertible then they correspond in a one-to-one manner.
In functional analysis, Banach *-algebras and C*-algebras are special types of Banach algebras with involutions.
Quaternion algebra, groups, semigroups
In a quaternion algebra, an (anti-)involution is defined by the following axioms: if we consider a transformation then it is an involution if
- (it is its own inverse)
- and (it is linear)
An anti-involution does not obey the last axiom but instead
This former law is sometimes called antidistributive. It also appears in groups as (xy)−1 = (y)−1(x)−1. Taken as an axiom, it leads to the notion of semigroup with involution, of which there are natural examples that are not groups, for example square matrix multiplication (i.e. the full linear monoid) with transpose as the involution.
نظرية الحلقات
In ring theory, the word involution is customarily taken to mean an antihomomorphism that is its own inverse function. Examples of involutions in common rings:
- complex conjugation on the complex plane, and its equivalent in the split-complex numbers
- taking the transpose in a matrix ring.
Group theory
In group theory, an element of a group is an involution if it has order 2; that is, an involution is an element a such that a ≠ e and a2 = e, where e is the identity element.[10] Originally, this definition agreed with the first definition above, since members of groups were always bijections from a set into itself; that is, group was taken to mean permutation group. By the end of the 19th century, group was defined more broadly, and accordingly so was involution.
A permutation is an involution if and only if it can be written as a finite product of disjoint transpositions.
The involutions of a group have a large impact on the group's structure. The study of involutions was instrumental in the classification of finite simple groups.
An element x of a group G is called strongly real if there is an involution t with xt = x−1 (where xt = x−1 = t−1 ⋅ x ⋅ t).
Coxeter groups are groups generated by a set S of involutions subject only to relations involving powers of pairs of elements of S. Coxeter groups can be used, among other things, to describe the possible regular polyhedra and their generalizations to higher dimensions.
Mathematical logic
The operation of complement in Boolean algebras is an involution. Accordingly, negation in classical logic satisfies the law of double negation: ¬¬A is equivalent to A.
Generally in non-classical logics, negation that satisfies the law of double negation is called involutive. In algebraic semantics, such a negation is realized as an involution on the algebra of truth values. Examples of logics that have involutive negation are Kleene and Bochvar three-valued logics, Łukasiewicz many-valued logic, the fuzzy logic 'involutive monoidal t-norm logic' (IMTL), etc. Involutive negation is sometimes added as an additional connective to logics with non-involutive negation; this is usual, for example, in t-norm fuzzy logics.
The involutiveness of negation is an important characterization property for logics and the corresponding varieties of algebras. For instance, involutive negation characterizes Boolean algebras among Heyting algebras. Correspondingly, classical Boolean logic arises by adding the law of double negation to intuitionistic logic. The same relationship holds also between MV-algebras and BL-algebras (and so correspondingly between Łukasiewicz logic and fuzzy logic BL), IMTL and MTL, and other pairs of important varieties of algebras (respectively, corresponding logics).
In the study of binary relations, every relation has a converse relation. Since the converse of the converse is the original relation, the conversion operation is an involution on the category of relations. Binary relations are ordered through inclusion. While this ordering is reversed with the complementation involution, it is preserved under conversion.
علم الحاسب
The XOR bitwise operation with a given value for one parameter is an involution on the other parameter. XOR masks in some instances were used to draw graphics on images in such a way that drawing them twice on the background reverts the background to its original state.
Two special cases of this, which are also involutions, are the bitwise NOT operation which is XOR with an all-ones value, and stream cipher encryption, which is an XOR with a secret keystream.
This predates binary computers; practically all mechanical cipher machines implement a reciprocal cipher, an involution on each typed-in letter. Instead of designing two kinds of machines, one for encrypting and one for decrypting, all the machines can be identical and can be set up (keyed) the same way.[11]
Another involution used in computers is an order-2 bitwise permutation. For example. a color value stored as integers in the form (R, G, B), could exchange R and B, resulting in the form (B, G, R): f(f(RGB)) = RGB, f(f(BGR)) = BGR.
الفيزياء
Legendre transformation, which converts between the Lagrangian and Hamiltonian, is an involutive operation.
Integrability, a central notion of physics and in particular the subfield of integrable systems, is closely related to involution, for example in context of Kramers–Wannier duality.
See also
References
- ^ Robert Alexander Adams, Calculus: Single Variable, 2006, ISBN 0321307143, p. 165
- ^ Russell, Bertrand (1903), Principles of mathematics (2nd ed.), W. W. Norton & Company, Inc, p. 426, ISBN 9781440054167, https://books.google.com/books?id=63ooitcP2osC&q=involution%20subject%3A%&pg=PR3
- ^ Kubrusly, Carlos S. (2011), The Elements of Operator Theory, Springer Science & Business Media, Problem 1.11(a), p. 27, ISBN 9780817649982, https://books.google.com/books?id=g-UFYTO8SbMC&pg=PA27.
- ^ Knuth, Donald E. (1973), The Art of Computer Programming, Volume 3: Sorting and Searching, Reading, Mass.: Addison-Wesley, pp. 48, 65
- ^ Zagier, D. (1990), "A one-sentence proof that every prime p ≡ 1 (mod 4) is a sum of two squares", American Mathematical Monthly 97 (2): 144, doi:.
- ^ أ ب A.G. Pickford (1909) Elementary Projective Geometry, Cambridge University Press via Internet Archive
- ^ J. V. Field and J. J. Gray (1987) The Geometrical Work of Girard Desargues, (New York: Springer), p. 54
- ^ Ivor Thomas (editor) (1980) Selections Illustrating the History of Greek Mathematics, Volume II, number 362 in the Loeb Classical Library (Cambridge and London: Harvard and Heinemann), pp. 610–3
- ^ H. S. M. Coxeter (1969) Introduction to Geometry, pp. 244–8, John Wiley & Sons
- ^ John S. Rose. "A Course on Group Theory". p. 10, section 1.13.
- ^ Goebel, Greg (2018). "The Mechanization of Ciphers". Classical Cryptology.
Further reading
- Ell, Todd A.; Sangwine, Stephen J. (2007). "Quaternion involutions and anti-involutions". Computers & Mathematics with Applications. 53 (1): 137–143. arXiv:math/0506034. doi:10.1016/j.camwa.2006.10.029. S2CID 45639619.
- Knus, Max-Albert; Merkurjev, Alexander; Rost, Markus; Tignol, Jean-Pierre (1998), The book of involutions, Colloquium Publications, 44, With a preface by J. Tits, Providence, RI: American Mathematical Society, ISBN 0-8218-0904-0
- Hazewinkel, Michiel, ed. (2001), "Involution", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
External links
 Media related to Involution at Wikimedia Commons
Media related to Involution at Wikimedia Commons