انعكاس (رياضيات)

أن تتابع الانعكاس على محورين متوازيين يسمى: "تحويل" (translation). انعكس الشكل البني فنتج الأخضر ثم انعكس الأخضر فأنتج الأزرق . والانتقال هو من البني إلى الأزرق.

أن تتابع الانعكاس على محورين غير متوازيين يسمى: "دوران" (rotation) حول نقطة التقاء المحورين

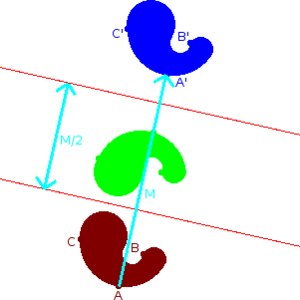
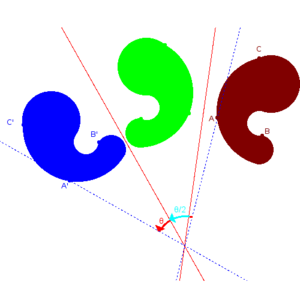
الانعكاس إنگليزية: Reflection أو Reflexion في الرياضيات، هي دالة التي تحول شكل ما إلى صورة مرآته (المعكوسة). فمثلا، انعكاس شكل الحرف "p" بالنسبة لخط أفقي (أو مرآة) يصبح بالشكل "q". لعكس مسطح ثنائي الأبعاد، يستعمل خط كمرآة و يُسمى محور الإنعكاس (axis of Reflection)، بينما يلزم لانعكاس جسم ثلاثي الأبعاد مثل القطة مستوى ثنائي الأبعاد مرآة. ويعتبر الانعكاس في بعض الأحيان حالة خاصة من حالات الانقلاب (inversion).

وبالمفهوم الهندسي، لإيجاد الانعكاس لنقطة ما، يتم إسقاط خط عمودي على الخط (أو المستوى) المستعمل كمحور الانعكاس، ثم مد الخط بشكل مستقيم في الجهة الأخرى من المحور وبنفس المسافة.

ولتحديد الانعكاس لرسم ما، يتم تحديد انعكاسات كل النقاط المؤلفة له على الناحية الأخرى من محور الانعكاس.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 ملاحظات

• القيام بانعكاس مرتين على نفس المحور يعود بنا إلى الشكل الأصلي.
• الانعكاس يحافظ على المسافات بين النقاط المعكوسة.
• أن الانعكاس لا يؤثر على النقاط الموجودة على المرآة أو على المحور.
• بعد الانعكاس في المرآة يكون أصغر ببعد واحد من الفضاء المعكوس (مثلاً إذا كانت المرآة موجودة في الفضاء الثلاثي الأبعاد فإن الصورة المعكوسة عليها تكون في الفضاء الثنائي الأبعاد وهكذا).

ومن هذه الملاحظات يمكننا تعريف الانعكاس كالآتي:

الإنعكاس هو دالة معكوسة نفسها متساوية الأبعاد لفضاء إقليدي بحيث نقاطها الثابتة هي فضاء أفيني كوديمي أول.^{[بحاجة لمصدر]}

 المعادلات

في حالة متجه a في الفضاء الإقليدي Rⁿ ، فإن معادلة الإنعكاس في المستوي الفائق من خلال المصدر المتعامد مع a هي:

$\mathrm {Ref} _{a}(v)=v-2{\frac {v\cdot a}{a\cdot a}}a$

بحيث v·a هي نتيجة ضرب متجه v في a ولاحظ ان الطرف الثاني في المعادلة هو ضعف اسقاط v على a ويمكن بسهولة إثبات:

• Ref_a(v) = -v إذا كانت v متوازية مع a و

• Ref_a(v) = v, إذا كانت v متعامدة مع a

وبما أن الإنعكاسات هذه هي ايزوميترية في فضاء إقليدي ذات مصدر محدد، فيكن تمثيلها بمصفوفة متعامدة والتي هي:

$R_{ij}=\delta _{ij}-2{\frac {a_{i}a_{j}}{\|a\|^{2}}}$

بحيث δ_ij هي دلتا كرونيكر. والمعادلة لإنعكاس في فضاء أفيني $v\cdot a=c$ هي:

$\mathrm {Ref} _{a,c}(v)=v-2{\frac {v\cdot a-c}{a\cdot a}}a.$

 انظر أيضاً

• انعكاس (فيزياء)
• تحويل
• انعكاس انزلاقي
• مجموعة افريزية (هندسة)

 وصلات خارجية

• الأنعكاس بالنسبة لخط على موقع cut-the-knot
• شرح الأنعكاس الثنائي الأبعاد
• شرح الأنعكاس الثلاثي الأبعاد
• Eric W. Weisstein, انعكاس at MathWorld.