البطاء المغناطيسي
البِطاء ،Hysteresis ظاهرة تكون فيها حالةُ جملة فيزيائية ذاتَ علاقة بتاريخها السابق، ويكون البطاء عادة على صورة تأخر استجابة مفعول فيزيائي عن المتغير الذي سبب حدوثه. ويحدث البطاء في حقول من العلم مختلفة، فالبطاء الميكانيكي يكون المتغير فيه الإجهاد stress، وتكون الاستجابة المتغيرة هي الانفعال أو التشوه strain. أما البطاء المغنطيسي فيحدث في المواد الحديدية المغنطيسية، ويكون المتغير فيه الحقلَ المغنطيسي (ح) وتكون الاستجابة المتغيرة التمغنط (مغ).[1]
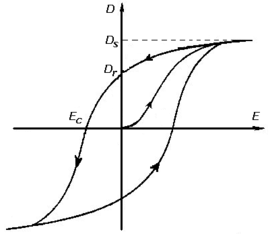
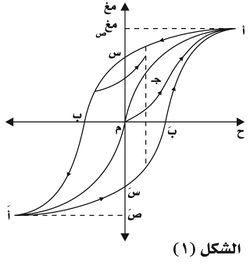
فإذا أخذت عينة غير ممغنطة من جسم حديدي المغنطيسية أو أزيل تمغنطها، وأخضعت لحقل مغنطيسي تتزايد شدته من الصفر فإن تمغنطها يتزايد من الصفر ببطء ثم بشدة ثم يتباطأ بعدها حتى يبلغ قيمة الإشباع مغص عند أ عندما تبلغ شدة الحقل المغنطيسي القيمة حع، ويتم ذلك وفق المنحني م جـ أ الذي يسمى منحني التمغنط الأولي. وعندما تُخفض قيمة الحقل إلى الصفر انطلاقاً من النقطة أ يتناقص التمغنط ببطء أشد من ازدياده في منحني التمغنط الأولي، ولا ينعدم هذا التمغنط بانعدام ح بل يحتفظ بتمغنط متبقٍ مغر. ولكي ينعدم يجب عندئذ أن يعكس اتجاه الحقل ح (وذلك بعكس اتجاه التيار المُمَغنط) ويُزاد في قيمته حتى يبلغ القيمة م ب = - حب، ويسمى هذا الحقل باسم الحقل القاهر coercive. وبالاستمرار في إنقاص ح تنعكس جهة مغ وتزداد شدته حتى تبلغ نقطة الإشباع أَ المناظرة للنقطة أ، وذلك عندما تساوي قيمة الحقل المغنطيسي (-حع). ويطلق على المنحني أرب أَ فرع التراجع.
وحين يُزاد الحقل مجدداً من القيمة ـ حع إلى القيمة + حع يرسم التمغنط الفرع أَ رَ بَ أ المناظر للفرع أ ر ب أََ بالنسبة إلى نقطة الأصل م، وينغلق منحني التمغنط مؤلفاً ما يسمى دورة البطاء المغنطيسي المبينة في الشكل. ودورة البطاء هذه هي الدورة العظمى، أما إذا لم تسمح قيمة ح ببلوغ الإشباع فتكون دورة البطاء دورة خاصة، وهناك عدد غير محدود من الدورات الخاصة، وتقع جميعاً ضمن الدورة العظمى. ويمكن الحصول على دورات خاصة تتناقص مساحاتها بالتدريج حتى تنعدم بجعل شدة التيار المتناوب الممغنط تتناقص تدريجياً حتى الصفر تقريباً، ويمكن استخدام هذه الطريقة لإزالة تمغنط المادة الحديدية المغنطيسية.
وإذا كانت دورات البطاء المغنطيسي المتناظرة المرتسمة بين الحقلين الحديين +حع و حع تستقر في أعقاب عدة دورات وتصبح قابلة للتراكب بعضها فوق بعض، فإن دورات البطاء اللامتناظرة المرتسمة، على سبيل المثال، بين الحقلين الحديين صفر و+حع تنزاح تدريجياً، ويسعى مركز ثقل الدورة إلى اللحاق بمنحنٍ يسمى المنحني اللابطائي، ويطلق على هذه الظاهرة اسم الزحف reptation، وإذا كان ن عدد الدورات اللامتناظرة فإن زحف الدورة يتغير إجمالاً كتغير لغ ن.
كذلك فإنه يمكن للصدمات والاهتزازات والتشوهات الميكانيكية أن تحدث للتمغنط في منطقة البطاء تغيرات لاعكوسة تكون أحياناً بالغة الأهمية، ويحدث الشيء نفسه بتغيرات درجة الحرارة.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
التاريخ
الآثار
في الهندسة
أنظمة التحكم

الدوائر الإلكترونية
تصميم واجهة المستخدم
في الميكانيكا
الرجوعية المرنة

Contact angle hysteresis
Adsorption hysteresis
Matric potential hysteresis
في المواد
البطاء الكهربائي والمغناطسيسي
البطاء المغناطيسي
إن البلورة الحديدية المغنطيسية الكاملة وذات الأبعاد الكبيرة (الحجم الكبير) لا تبدي عملياً ظاهرة البطاء المغنطيسي التي تنجم عن مختلف أنواع عيوب هذه البلورات، وعلى هذا يُعدّ الحجم الصغير عيباً، فالحبيبات الدقيقة جداً التي أبعادها من مرتبة 0.01 مكرون (أي 10-8 متر) تمتلك حقلاً مغنطيسياً قاهراً عالياً، وتتمتع بعزم مغنطيسي متغيّر القيمة يشغل اتجاهين مستقريْن متوازيين ومتعاكسين؛ وللانتقال من أحدهما إلى الآخر يجب تطبيق حقل مغنطيسي كبير كبراً كافياً لكي يجتاز العزم حاجز الكمون الذي يفصل بين الاتجاهين والناجم عن اللاتناحي anisotropy في الشكل، أو عن اللاتناحي المغنطيسي البلوري للحبيبة. وتتكوّن العيوب الأساسية في المواد الضخمة، ولاسيما في المواد الكثيرة البلورات، من تلاصق الحبيبات، ومن الفجوات ومن وجود مواد أقل مغنطيسية أو أكثر مغنطيسية من الركازة matrix ومن الإجهادات الداخلية المتوزعة توزعاً غير منتظم. ويكون أثر هذه العيوب أكثر بروزاً كلما قربت أبعادها من 0.1 مكرون (من أجل الحديد)؛ كما أن أثر هذه العيوب يزداد أيضاً كلما ازداد اللاتناحي المغنطيسي والتخصُّر المغنطيسي magnetostriction للجسم.
وتوصف المادة الحديدية المغنطيسية بأنها قاسية إذا كان الحقل القاهر حب كبيراً وتكون دورة البطاء عندئذ عريضة؛ أما إذا كان حب صغيراً، ومن ثم تكون دورة البطاء ضيقة، فتوصف المادة حينئذ بأنها لينة. وعلى العموم، يكون التمغنط المتبقي في أي دورة كسراً من تمغنط الإشباع يقع بين 0.5 و1، أما الحقل القاهر فيتغير في مجالات عريضة جداً من 0.01 أورستد oersted من أجل الخليطة سوبرمالُويْ supermalloy (النيكل 78%، المولبدين 4%، والحديد 18% ) حتى 10000 أورستد في حالة خليطة البلاتين والكوبلت PtCo وخليطة السماريوم Samarium والكوبالت SmCo.
وللحصول على مادة لينة ببطاء ضئيل يجب استعمال مادة شديدة النقاوة وذات تخصُّر مغنطيسي ضعيف ولاتناحٍ مغنطيسي بلوري ضئيل، ويتطلب عكس ذلك الحصول على مادة قاسية صالحة لمغنطيس دائم. وقد بذلت المساعي لأجل التطبيقات الصناعية في تهيئة مواد لها صفات مغنطيسية خاصة باستعمال خلائط مختلفة.
ضياع الطاقة بالبطاء المغنطيسي
تسخن قطعة الحديد في أثناء دورة البطاء وتتناسب الطاقة المتبددة (طا) في أثناء دورة بطاء واحدة مع حجم الجسم الحديدي ومع مساحة دورة البطاء، ولما كان مُستَخدِم المواد الممغنطة يهتم بحقل التحريض (تح) أكثر مما يهتم بالتمغنط (مغ) فإنه يرسم دورة البطاء بالإحداثيين (تح، مع). وهناك قانون تجريبي اقترحه شتايْنمِتْز Steinmetz وهو طا= ب تح ع- α حيث ب و α ثابتان يتعلقان بالمادة المدروسة، وتقرب قيمة α كثيراً من 1.6 أما (ب) فإنها في الواحدات العملية نحو بضع عشرات أومئات في المواد اللينة وبضعة ألوف في المواد القاسية.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
تطبيقات البطاء المغنطيسي
تتصف المواد القاسية بتمغنط متبق وحقل قاهر شديدين، لذلك تستعمل هذه المواد في صنع المغانط الدائمة، فتعطى هيئة قضيب يوضع في داخل ملف يمر فيه تيار كهربائي قوي، وحين يخرج القضيب يحتفظ بتمغنط قريب من تمغنط الإشباع. وأكثر المواد استعمالاً في هذا الصدد الفولاذ المسقي وخليطة ألنيكو Alnico (ألمنيوم 8%، كوبلت 24%، نيكل 14%، حديد 51%، نحاس 3%)، ومن الواضح أن زوال التمغنط يبدأ في الطرفين ثم يزحف نحو الوسط إلا إذا كان المغنطيس على هيئة حذوة حصان ومجهزاً بحافظة تعدم الحقل المزيل للتمغنط. وللحصول على حقل مغنطيسي شديد جداً ضمن حجم صغير جداً في الهواء يلجأ إلى صنع مغانط كهربائية، يتألف كل منها من قطعتين معدنيتين متقابلتين وجهاً لوجه تؤلفان قطبي المغنطيس الكهربائي الشمالي والجنوبي، وتفصل بينهما فجوة ضيقة تسمى الحجيرة. وللمغانط الكهربائية استعمالات عديدة في غير مجال البحث العلمي، منها الأجراس الكهربائية ورفع الأثقال.
غير أن لظاهرة البطاء المغنطيسي أثراً ضاراً في ميادين أخرى وذلك بسبب تسخينها للمادة؛ ففي نوى المحولات والمنوبات التي تعمل في التيارات المتناوبة تحدث دورة البطاء عدداً من المرات في الثانية يساوي تواتر التيار، مما يؤدي إلى خسران كبير في الطاقة وتسخين شديد في النواة، لذا تصنع هذه النوى من مواد لينة مغنطيسياً تتصف دورة بطائها بتمغنط متبق وحقل قاهر صغيرين، وأكثر المواد استعمالاً لهذا الغرض خلائط الحديد بالنيكل مثل نوميتال numetal (نيكل 75%، حديد 17%، نحاس 5%، كروم أو منغنيز 2%) ومثل البرمالوي permalloy (نيكل 75%، حديد 22%، مولبدين أو منغنيز 5%).
البطاء الكهربائي
Liquid-solid phase transitions
في علم الأحياء
بيولوجيا الخلية والمورثات
علم الأعصاب
فسيولوجيا الجهاز التنفسي
في الاقتصاد
ارتفاع البطالة بشكل دائم
نظرية الألعاب وضوابط رأس المال
التطبيقات
اعتبارات إضافية
نماذج للبطاء المغناطيسي
الطاقة
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
انظر أيضا
- Remanence
- Hysteresivity
- Path dependence
- Backlash (engineering)
- Metastability
- Bean's critical state model
المصادر
- ^ توفيق قسام. "ماجد عبد الفتاح أول متحدث رسمي باسم الرئاسة في مصر". الموسوعة العربية. Retrieved 2011-05-24.
قراءات إضافية
- Mark Krasnosel'skii and Alexei Pokrovskii, Systems with Hysteresis, Springer-Verlag, New York, 1989.
- Isaak D. Mayergoyz, Mathematical Models of Hysteresis and their Applications: Second Edition (Electromagnetism), Academic Press, 2003.
- The Science of Hysteresis (3-volume set), ed. by Isaak D. Mayergoyz, Giorgio Bertotti, Academic, 2005.