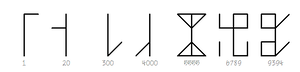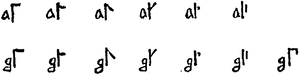الأعداد السيسترسية

Numbers written with Cistercian numerals. From left to right: 1 in units place, 2 in tens place (20), 3 in hundreds place (300), 4 in thousands place (4,000), then compound numbers 5,555, 6,789, 9,394.
أنظمة الأرقام حسب الثقافة
الأرقام الهندية العربية
العربية المغربية
العربية المشرقية
الخمير 		العائلة الهندية
البراهمية
التايلندية
أرقام شرق آسيا
الصينية
سوژو
عصي العد 		اليابانية
الكورية 
الأرقام الأبجدية
أبجد
الأرمنية
السيريلية
جعيز 		العبرية
اليونانية (Ionian)
أريابهاتا
 
أنظمة أخرى
Attic
البابلية
المصرية
الإتروسكية 		المايا
الرومانية
Urnfield
قائمة مواضيع نظم الأرقام
Positional systems by base
عشري (10)
2, 4, 8, 16, 32, 64
1, 3, 9, 12, 20, 24, 30, 36, 60, more…
عرض • نقاش • تعديل
The entry for the word 'aqua' in an early-thirteenth-century concordance from Brussels. Each character is a page/column number. These early Cistercian forms, with 3 and 4 swapped for 7 and 8, plus single and double dots for 5 and 6 and a triangular 9, are found in only one other surviving manuscript. The numbers are,
21, 41, 81, 85, 106, 115,
146, 148, 150, 169, 194, 198,
267, 268, 272, 281, 284, 295,
296, 317, 343, 368, 378, 387,
403, 404, 405, 420, 434, 435,
436, 446, 476, 506, 508, 552,
566, 591, 601, 604, 628, 635,
659, 678, 686, 697, 724, 759,
779, 783, 803, 818, 834, 858.

الأعداد السيسترسية أو "الشيفرة" حسب مصطلحات القرن التاسع عشر، طورت من قبل نظام الرهبنة السيسترسي في بدايات القرن الثالث عشر تقريباً في نفس الوقت الذي قدمت فيه الأرقام العربية إلى شمال غرب أوروپا. إنها أكثر تعقيداً من العربية أو الأرقام الرومانية، يمكن لرمز واحد أن يشير لأي عدد صحيح ما بين 1 وحتى 9،999. أساس الأرقام هو عصا إما أفقية أو شاقولية، ووضعية الرقم على العصا تشير إلى قيمة المنزلة (آحاد، عشرات، مئات، آلاف). تكون الأرقام مركبة على عصا واحدة للإشارة لأرقام أعقد. توقف السيسترسيون عن استخدام هذا النظام مفضلين عليه نظام الأرقام العربية، ولكن استمر استخدامه بشكل طفيف خارج النظام حتى بدايات القرن العشرين.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

التاريخ

كان واضحاً أن الأرقام وفكرة تشكيلها على وصلات بناءً على نظام ترقيم من منزلتين (1-99) قد وصل إلى السيسترسية عن طريق جون من باسينگستوك، رئيس شمامسة ليسيستر، والذي يبدو أنه بناها على الموجز الإنگليزي من القرن العشرين (آرس نوتاريا). [nb 1] في الشهادات الأولى، في أديرة مقاطعة هاينوت، لم يستخدم النظام السيسترسي لأرقام أكبر من 99 ولكنه توسع بعد فترة قصيرة إلى أربع منازل فوصلت الأرقام إلى 9،999. [2]


يعود تاريخ المخطوطات القليلة الباقية من السيسترسية إلى ما بين القرنين الثالث عشر والخامس عشر وتغطي منطقة من إنگلترة إلى إيطاليا، نورماندي إلى السويد. لم تستخدم الأرقام لأغراض حسابية أو الكسور أو المحاسبة ولكن للدلالة على الأعوام، التصفيح (ترقيم الصفحات)، تقسيم النصوص، ترقيم الملاحظات والقوائم الأخرى، الفهارس، مواعيد عيد الفصح، وأرقام الأسطر في النوتات الموسيقية. [3]


Samples of mixed alphabetic-Cistercian notation used for foliation in a late thirteenth-century manuscript. Shown are a1 to a6 and g1 to g7.

رغم أن استعمالها كان مقتصراً على النظام السيسترسي، ظهر استخدام لها خارجه. ورد استخدام كل من الأعداد السيسترسية و العربية الهندية في أطروحة نورمندية تعود إلى أواخر القرن الخامس عشر. في إحدى الحالات المعروفة، حفرت الأعداد السيسترسية على أغراض، مشيرةً إلى الترقيم والزوايا وأعداد أخرى على اسطرلاب بريسيليوس الذي يعود إلى القرن الرابع عشر والذي صنع في پيكاردي الفرنسية. [4]

بعد توقف السيسترسية عن استخدام نظام الأعداد، ظهرت استخدامات قليلة له خارج النظام. في عام 1533، أدخل هنريك كورنيليوس أگريپا ڤون نيتيشيم توصيفاً لتلك الأرقام في مؤلفه ثلاثة كتب عن الفلسفة الباطنية. [5]

استخدمت الأعداد السيسترسية من قبل معايري النبيذ في منطقة بروج حتى القرن الثامن عشر على الأقل. [6][7][8]

في أواخر القرن الثامن عشر، اعتمد فرسان الصليب الأحمر في پاريس الأعداد لاستخدام مجهول، وفي بداية العرن العشرين، راقت لـ النازية فكرة استخدام الأعداد في الترميز الآري. [3][9][10][11]

الخبير الحديث في الأعداد السيسترسية هو ديڤيد كينگ.[12][1]


الشكل

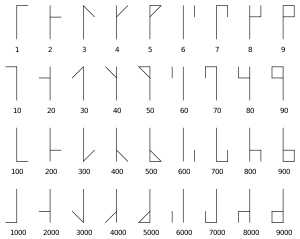
The vertical forms of the digits (1–9, 10–90, 100–900 and 1,000–9,000), with an innovative form of 5 as engraved on an early-sixteenth-century Norman astrolabe.

كانت العصا الأفقية أكثر شيوعاً حين كانت تستخدم الأعداد بين السيسترسيين. بينما استخدمت العصا الشاقولية فقط في شمال فرنسا في القرنين الرابع عشر والخامس عشر. أثناء إعادة إحياء النظام في القرنين الثامن عشر والعشرين في فرنسا وألمانيا استخدمت العصا الأفقية. هناك أيضاً تصنيف تاريخي يدل على أن الزاوية تدل على قيمة المنزلة. القيم المنزلية المعروضة هنا أكثر شيوعاً في السيسترسية والوحيدة المستخدمة لاحقاً. [3][13] استخدام بدائل رسومية بعصا أفقية، [nb 2] أول خمسة أرقام هي ꜒ 1, ꜓ 2, ꜒꜓ 3, ꜓꜒ 4, ꜍ 5. وعكسها يعطي العشرات ˥ 10, ˦ 20, ˦˥ 30, ˥˦ 40, ꜈ 50 . وقلبها يعطي المئات ꜖ 100, ꜕ 200, ꜖꜕ 300, ꜕꜖ 400, ꜑ 500 . أما عكسها وقلبها في آن معاً يعطي الآلاف ˩ 1,000, ˨ 2,000, ˨˩ 3,000, ˩˨ 4,000, ꜌ 5,000. لذا فإن ⌶ (الرقم 1 في كل زاوية) هو الرقم 1،111. (اختلفت الصيغ نفسها حسي التاريخ والدير، على سبيل المثال، الأرقام الموجودة هنا الدالة على 3 و 4 استبدلت في بعض المخطوطات بأشكال 6 و7، و قد ترسم الـ 5 مع نقطة في الأسفل (꜎ etc.)، أو مع شطب صغير شاقولي مكان النقطة، أو مع مثلث يضم العصوين ، والذي في مخطوطات أخرى أشار إلى 9.) [13][1]


A fourteenth-century Norman manuscript that used only Cistercian numerals. These were horizontal to fit the flow of the text. Note the round form of the digit 9. Numbers were later retranscribed with Hindu-Arabic digits in the margin notes: here we see 4,484, 715 and 5,199.

كانت الأرقام الأفقية مثلها، ولكنها استدارت 90 درجة بعكس عقارب الساعة. ( ˾ ل 1, ⌐ ل 10, ⌙ل 100—أي ⌴ ل 101—and ¬ for 1,000, كما يظهر في اليسار)[2][1]


حذف رقم من زاوية كان يعني قيمة الصفر من أجل تكوين العشرة، ولكن لم يكن هناك الرقم صفر. (لم يكن هناك عصا فارغة). [14]


الأعداد العليا

حين انتشرت الأعداد خارج النظام في القرنين الخامس عشر والسادس عشر، وجدت أرقام الملايين عبر تركيب أرقام "الآلاف". مثلاً، أظهرت أطروحة نورماندية عن الحساب تعود لأواخر القرن الخامس عشر رقم 10،000 كربط بين ⌋ "1,000" موجوداً تحدت ⌉ "10" (وكذلك الحال بالنسبة إلى أرقام أكبر)،وفي نوڤيوماگاس عام 1539، كتب "المليون" عبر رسم ¬ "1,000" تحت واحد آخر مثله. [15] احتوت رسومات سيسترسية أخرى تعود لأواخر القرن الثالث عشر على أرقام أفقية مختلفة للمضاعفات الدنيا للعشرة عما تحمله الأرقام الشاقولية للمضاعفات الكبرى للعشرة، ولكن يحتمل أن المضاعفة قد بدأت تستخدم في ذلك الوقت، كانت قد تغطي أرقاماً إلى عشرات الملايين (أفقي 100 to 103، شاقولي 104 to 107). [16] استخدم عالم رياضيات في القرن السادس عشر الأرقام الشاقولية للقيم الاعتيادية، والأرقام الأفقية للملايين وأدارها 45 درجة أكثر عكس عقارب الساعة للمليارات و90 درجة أخرى للتريليونات، لم يكن واضحاً كيف يشار إلى مضاعفات العشرة ولم يعتمد هذا الأسلوب أحد آخر. [17]


Notes

  1. ^
    A copy of the ciphers in a treatise on penmanship (c. 1300 CE) commonly attributed to John of Tilbury, with the corresponding Basingstoke numerical values.
    ادعى كاتب سيرة حياة باسينگستوك أنه تعلم نظامه من معلمه في أثينا. ولكن لا يوجد مواز لذلك في نظام الأرقام اليوناني. على الأغلب أن باسينگستوك حصل على فكرة نظام الترقيم الأبجدي في اليونان وطبقة على آرس نوتاريا إنكليزية، مثل التي تظهر على اليمين، تنسب إلى جون من تيلبيري. [1]
  2. ^ Cistercian numerals are not supported by Unicode, and are here substituted with Chao tone letters. Depending on the fonts you have installed, it may be that only the ones and twos will display properly. (The Under-ConScript Unicode Registry has tentatively assigned the units to PUA values U+EBA1 to U+EBAF.)

References

  1. ^ أ ب ت ث Chrisomalis, Stephen (2010). Numerical notation : a comparative history. Cambridge: Cambridge University Press. p. 350. doi:10.1017/CBO9780511676062. ISBN 978-0-511-67683-3. OCLC 630115876.
  2. ^ أ ب King, David A. (2001). The Ciphers of the Monks : a: a forgotten number-notation of the Middle Ages. Stuttgart: F. Steiner. pp. 16, 29, 34, 41. ISBN 3-515-07640-9. OCLC 48254993.
  3. ^ أ ب ت King, David (1993). "Rewriting history through instruments: The secrets of a medieval astrolabe from Picardy". In Anderson, R. G. W.; Bennett, J. A. & Ryan, W. F. (eds.). Making Instruments Count: Essays on Historical Scientific Instruments Presented to Gerard L'Estrange Turner. University of Michigan. ISBN 978-0860783947.
  4. ^ King, David A. (1992). "The Ciphers of the Monks and the Astrolabe of Berselius Reconsidered". In Demidov, Sergei S.; Rowe, David; Folkerts, Menso & Scriba, Christoph J. (eds.). Amphora. Basel: Birkhäuser. pp. 375–388. doi:10.1007/978-3-0348-8599-7_18. ISBN 978-3-0348-8599-7.
  5. ^ Agrippa von Nettesheim, Heinrich Cornelius (1533). "De notis Hebraeorum et Chaldaeorum". De Occulta Philosophia (in اللاتينية). p. 141.
  6. ^ Meskens, Ad; Bonte, Germain; De Groot, Jacques; De Jonghe, Mieke & King, David A. (1999). "Wine-Gauging at Damme [The evidence of a late medieval manuscript]". Histoire & Mesure. 14 (1): 51–77. doi:10.3406/hism.1999.1501.
  7. ^ Beaujouan, Guy (1950). "Les soi-disant chiffres grecs ou chaldéens (XIIe – XVIe siècle)". Revue d'histoire des sciences (in الفرنسية). 3 (2): 170–174. doi:10.3406/rhs.1950.2795.
  8. ^ Sesiano, Jacques (1985). "Un système artificiel de numérotation au Moyen Age". In Folkerts, Menso & Lindgren, Uta (eds.). Mathemata : Festschrift für Helmuth Gericke (in الفرنسية). Stuttgart: F. Steiner Verlag. ISBN 3-515-04324-1. OCLC 12644728.
  9. ^ King (2001:243, 251)
  10. ^ De Laurence, Lauron William (1915). The Great Book of Magical Art, Hindu Magic and East Indian Occultism (in الإنجليزية). Chicago: De Laurence Co. p. 174.
  11. ^ Beard, Daniel Carter (1918). The American boys' book of signs, signals and symbols. New York Public Library. Philadelphia : Lippincott. p. 92.
  12. ^ King, David (1995). "A forgotten Cistercian system of numerical notation". Citeaux Commentarii Cistercienses. 46 (3–4): 183–217.
  13. ^ أ ب King (2001:39)
  14. ^ King (2001:427)
  15. ^ King (2001:156, 214)
  16. ^ King (2001:182–185)
  17. ^ King (2001:210)

External links

تمّ الاسترجاع من "https://www.marefa.org/w/index.php?title=الأعداد_السيسترسية&oldid=2287678"