إسقاط متواز
في الجبر الخطي والتحليل الدالي، الإسقاط، هو تحويل خطي لـP من الفضاء المتجهي إلى نفسها مثل P 2 = P. ويعني هذا، أنه كلما تم تطبيق P مرتين على أي قيمة، فإنها ستعطي نفس النتيجة إذا ما تم تطبيقها مرة واحدة. وتترك الصورة بلا تغيير.[1] على الرغم من كونه مجرد ملخص ، فإن هذا التعريف لـ "الإسقاط" يضفى الطابع الرسمي ويعمم فكرة الإسقاط الهندسي. كما يمكن اعتباره أثراً للإسقاط على الأجسام الهندسية بفحص تأثير الإسقاط على النقاط الموجودة على الجسم.
أمثلة مبسطة
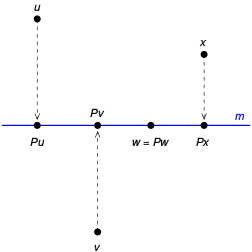
الإسقاط العمودي
هذا الإسقاط يشمل أساليب تمثيل هندسي مثل طريقة مونج والأكسونومتري العمودية (ايزوميتري، ديميتري،تريميتري)
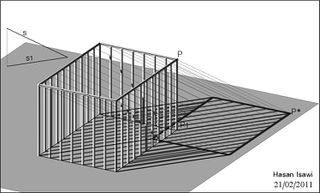
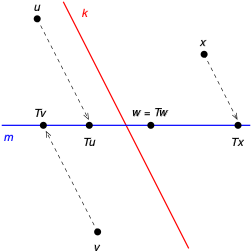
الإسقاط المائل
حسب التوازي أو عدمة بين أحد المستويات الاحداثية (xy, yz, xz) ومستوى الإسقاط π، يمكن تصنيف الإسقاط المائل إلى نوعين من الأكسونومتري:
- اكسونومتري كافاليرا، عندما يكون هناك توازي أو تطابق بين أحد المستويات الإحداثية ومستوى الاسقاط π.
- اكسونومتري عامة، عندما لا يوجد هناك توازي بين أحد المستويات الاحداثية مع π.
الخصائص والتصنيف
الصيغ الأساسية
الإسقاطات على الفضاء المتجهي المعياري
التطبيقات
تلعب الإسقاطات (العمودية وغيرها) دوراً رئيسياً في الخوارزميات لبعض مشاكل الجبر الخطية:
- QR decomposition (see Householder transformation and Gram–Schmidt decomposition);
- Singular value decomposition
- Reduction to Hessenberg form (the first step in many eigenvalue algorithms)
- الانكفاء الخطي
- Projective elements of matrix algebras are used in the construction of certain K-groups in Operator K-theory
انظر أيضاً
- Centering matrix, which is an example of a projection matrix.
- Orthogonalization
- Invariant subspace
- Properties of trace
- Dykstra's projection algorithm to compute the projection onto an intersection of sets
الهوامش
- ^ Meyer, pp 386+387
المصادر
- Banerjee, Sudipto; Roy, Anindya (2014), Linear Algebra and Matrix Analysis for Statistics, Texts in Statistical Science (1st ed.), Chapman and Hall/CRC, ISBN 978-1420095388
- Dunford, N.; Schwartz, J. T. (1958). Linear Operators, Part I: General Theory. Interscience.
- Meyer, Carl D. (2000). Matrix Analysis and Applied Linear Algebra. Society for Industrial and Applied Mathematics. ISBN 978-0-89871-454-8.
وصلات خارجية
- MIT Linear Algebra Lecture on Projection Matrices at YouTube, from MIT OpenCourseWare
- Linear Algebra 15d: The Projection Transformation at YouTube, by Pavel Grinfeld.
- Planar Geometric Projections Tutorial – a simple-to-follow tutorial explaining the different types of planar geometric projections.