نظرية النمط

في الرياضيات، المنطق، المعلوماتية، نظرية النمط هي أي نظام شكلي بإمكانه القيام مكان نظرية المجموعات البسيطة، أو دراسة التشكيل بشكل عام، وهي أيضاً منهج لبناء المنطق الصوري توضع بواسطته تفرقة بين الموضوعات ذات المستويات المختلفة (الأنماط)، ويهدف هذا المنهج إلى استبعاد المفارقات أو التناقضات من المنطق ونظرية الأعداد وكان إرنست شرودر أول من وضع نظرية الأنماط، وطبقها على منطق الفئات (1890)، وفي الأعوام 1908 - 1910 بنى برتراند رسل نسقاً تفصيلياً من نظرية الأنماط وطبقة على أساس التفرقة (طبقاً للأنماط) بين :

الافراد (نمط 1)

الصفات (نمط 2)

صفات الصفات (نمط 3)

وكذلك أدخل راسل تقسيم الأنماط إلى رتب، وليست نظرية النمط سوى واحدة من المناهج لإزالة التناقضات عن الأبنية في نظرية التعدد والمنطق الصوري وصاغ برتراند رسل نظرية النمط وكان ذلك بسبب اكتشافه تعارضا paradoxon في نظرية المجموعات البسيطة سمية بمفارقة رسل.

تعريف النمط: هو أساس تكرار قيمة، إما بالشكل أو بالأرقام.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

مثال: نحو اللغة الطبيعية

نبدأ بمثال لتشجيع التعريفات الجبرية التالية.

أتمتة النحو

مولدو النحو

	1x	1y	2x	2y	3x	3y	4x	4y	5x	5y	6x	6y	7x	7y	8x	8y	9x	9y	10x	10y	11x	11y	12x	12y
1x	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	1	-	-
1y		-	1	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
2x			-	1	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
2y				-	1	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
3x					-	-	-	-	-	-	-	-	-	1	-	-	-	-	-	-	-	-	-	-
3y						-	1	-	-	-	-	-	-	-	1	-	-	-	-	-	-	-	-	-
4x							-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
4y								-	1	-	1	-	-	-	-	-	-	-	-	-	-	-	-	-
5x									-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
5y										-	1	-	-	-	-	-	-	-	-	-	-	-	-	-
6x											-	-	-	-	-	-	-	-	-	-	-	-	-	-
6y												-	1	-	-	-	-	-	-	-	-	-	-	-
7x													-	1	-	-	-	-	-	-	-	-	-	-
7y														-	-	-	-	-	-	-	-	-	-	-
8x															-	-	-	-	-	-	-	-	-	-
8y																-	1	-	-	-	-	-	-	-
9x																	-	-	-	-	-	-	-	-
9y																		-	1	-	-	-	-	-
10x																			-	-	-	-	-	-
10y																				-	1	-	-	-
11x																					-	1	-	-
11y																						-	1	-
12x																							-	-
12y																								-

الأسس الجبرية

مدفوعين بالمثال، فإن لدينا التعريفات التالية:

1. A generator $g{\in }G$ , drawn as

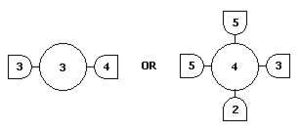
is the primitive of Pattern Theory that generates the observed signal. Structurally, it is a value with interfaces, called bonds $b{\in }B$ , which connects the $g$ 's to form a signal generator. 2 neighboring generators are connected when their bond values are the same. Similarity self-maps $s{\in }S$ s: G -> G express the invariances of the world we are looking at, such as rigid body transformations, or scaling.

2. Bonds glue generators into a configuration, c, which creates the signal against a backdrop Σ, with global features described locally by a bond coupling table called $\rho$ . The boolean function $\rho$ is the principal component of the regularity 4-tuple <G,S, $\rho$ ,Σ>, which is defined as

\rho (c)=\prod _{{\text{neighboring bonds }}b',b''\in c}\rho (b',b'').

$\rho$ seems to capture the notion of allowable generator neighbors. That is, Regularity is the law of the stimulus domain defining, via a bond table, what neighbors are acceptable for a generator. It is the laws of the stimulus domain. Later, we will relax regularity from a boolean function to a probability value, it would capture what stimulus neighbors are probable.

Σ is the physical arrangement of the generators. In vision, it could be a 2-dimensional lattice. In language, it is a linear arrangement.

3. An image (C mod R) captures the notion of an observed Configuration, as opposed to one which exists independently from any perceptual apparatus. Images are configurations distinguished only by their external bonds, inheriting the configuration’s composition and similarities transformations. Formally, images are equivalence classes partitioned by an Identification Rule "~" with 3 properties:

ext(c) = ext(c') whenever c~c'
sc~sc' whenever c~c'
sigma(c1,c2) ~ sigma(c1',c2') whenever c1~c1', c2~c2' are all regular.

A configuration corresponding to a physical stimulus may have many images, corresponding to many observer perception's identification rule.

4. A pattern is the repeatable components of an image, defined as the S-invariant subset of an image. Similarities are reference transformations we use to define patterns, e.g. rigid body transformations. At first glance, this definition seems suited for only texture patterns where the minimal sub-image is repeated over and over again. If we were to view an image of an object such as a dog, its is not repeated, yet seem like it seems familiar and should be a pattern. (Help needed here).

5. A deformation is a transformation of the original image that accounts for the noise in the environment and error in the perceptual apparatus. Grenander identifies 4 types of deformations: noise and blur, multi-scale superposition, domain warping, and interruptions.

المثال الثاني Directed boundary

Configuration

Image

Generators

This configuration of generators generating the image is created by primitives woven together by the bonding table, and perceived by an observer with the identification rule that maps non "0" & "1" generators to a single boundary element. Nine other undepicted generators are created by rotating each of the non-"0"&"1" generators by 90 degrees. Keeping the feature of "directed boundaries" in mind, the generators are cooked with some thought and is interpreted as follows: the "0" generator corresponds to interior elements, "1" to the exterior, "2" and its rotations are straight elements, and the remainder are the turning elements.

With Boolean regularity defined as Product (all nbr bonds), any configurations with even a single generator violating the bond table is discarded from consideration. Thus only features in its purest form with all neighboring generators adhering to the bond table are allowed. This stringent condition can be relaxed using probability measures instead of Boolean bond tables.

p(c)=\prod _{{\text{neighboring bonds }}b',b''\in c}A(b',b'')

The new regularity no longer dictates a perfect directed boundary, but it defines a probability of a configuration in terms of the Acceptor function A(). Such configurations are allowed to have impurities and imperfections with respect to the feature of interest.

With the benefit of being given generators and complete bond tables, a difficult part of pattern analysis is done. In tackling a new class of signals and features, the task of devising the generators and bond table is much more difficult.

Again, just as in grammars, identifying the generators and bond tables require some thought. Just as subtle is the fact that a configuration is not the signal we observe. Rather, we observe its image as silhouette projections of the identification rule.

جدول حقيقة الروابط البولية
قيم الروابط	0	1	2	3	4	5
0	1	—	—	—	1	—
1		1	—	—	—	1
2			—	1	—	—
3				—	—	—
4					—	—
5						—

العشوائية الداخلية

Pattern Theory defines order in terms of the feature of interest given by p(c).

Energy(c) = −log P(c)

الإحصاء

Grenander's Pattern Theory treatment of Bayesian inference in seems to be skewed towards on image reconstruction (e.g. content addressable memory). That is given image I-deformed, find I. However, Mumford's interpretation of Pattern Theory is broader and he defines PT to include many more well-known statistical methods. Mumford's criteria for inclusion of a topic as Pattern Theory are those methods "characterized by common techniques and motivations", such as the HMM, EM algorithm, dynamic programming circle of ideas. Topics in this section will reflect Mumford's treatment of Pattern Theory. His principle of statistical Pattern Theory are the following:

Use real world signals rather than constructed ones to infer the hidden states of interest.
Such signals contain too much complexity and artifacts to succumb to a purely deterministic analysis, so employ stochastic methods too.
Respect the natural structure of the signal, including any symmetries, independence of parts, marginals on key statistics. Validate by sampling from the derived models by and infer hidden states with Bayes’ rule.
Across all modalities, a limited family of deformations distort the pure patterns into real world signals.
Stochastic factors affecting an observation show strong conditional independence.

Conditional probability for local properties

N-gram Text Strings: See Mumford's Pattern Theory by Examples, Chapter 1.

MAP ~ MDL (MDL offers a glimpse of why the MAP probabilistic formulation make sense analytically)

Conditional probability for hidden-observed states

Bayes Theorem for Machine translation

Supposing we want to translate French sentences to English. Here, the hidden configurations are English sentences and the observed signal they generate are French sentences. Bayes theorem gives p(e|f)p(f) = p(e, f) = p(f|e)p(e) and reduces to the fundamental equation of machine translation: maximize p(e|f) = p(f|e)p(e) over the appropriate e (note that p(f) is independent of e, and so drops out when we maximize over e). This reduces the problem to three main calculations for:

p(e) for any given e, using the N-gram method and dynamic programming
p(f|e) for any given e and f, using alignments and an expectation-maximization (EM) algorithm
e that maximizes the product of 1 and 2, again, using dynamic programming

The analysis seems to be symmetric with respect to the two languages, and if we think can calculate p(f|e), why not turn the analysis around and calculate p(e|f) directly? The reason is that during the calculation of p(f|e) the asymmetric assumption is made that source sentence be well formed and we cannot make any such assumption about the target translation because we do not know what it will translate into.

We now focus on p(f|e) in the three-part decomposition above. The other two parts, p(e) and maximizing e, uses similar techniques as the N-gram model. Given a French-English translation from a large training data set (such data sets exists from the Canadian parliament):

       NULL   And    the    program      has    been    implemented
                     Le     programme    a ete     mis en application

the sentence pair can be encoded as an alignment (2, 3, 4, 5, 6, 6, 6) that reads as follows: the first word in French comes from the second English word, the second word in French comes from the 3rd English word, and so forth. Although an alignment is a straightforward encoding of the translation, a more computationally convenient approach to an alignment is to break it down into four parameters:

Fertility: the number of words in the French string that will be connected to it. E.g. n( 3 | implemented ) = probability that “implemented” translates into three words – the word's fertility
Spuriousness: we introduce the artifact NULL as a word to represent the probability of tossing in a spurious French word. E.g. $p 1$ and its complement will be $p 0 = 1 - p 1$ .
Translation: the translated version of each word. E.g. t(a | has ) = translation probability that the English "has" translates into the French "a".
Distortion: the actual positions in the French string that these words will occupy. E.g. d( 5 | 2, 4, 6 ) = distortion of second position French word moving into the fifth position English word for a four-word English sentence and a six-word French sentence. We encode the alignments this way to easily represent and extract priors from our training data and the new formula becomes

{\begin{aligned}p(f|e)&={\text{Sum over all possible alignments an of }}p(a,f|e)\\&=n_{0}(v_{0}|\sum _{j=1}^{l}{v_{j}})\cdot \prod _{j=1}^{l}n(v_{j}|e_{j})v_{j}!\cdot \prod _{j=1}^{m}t(f_{j}|e_{a_{j}})\cdot \prod _{j:a_{j}\not =0}^{m}d(j|a_{j},l,m)\end{aligned}}

For the sake of simplicity in demonstrating an EM algorithm, we shall go through a simple calculation involving only translation probabilities t(), but needless to say that it the method applies to all parameters in their full glory. Consider the simplified case (1) without the NULL word (2) where every word has fertility 1 and (3) there are no distortion probabilities. Our training data corpus will contain two-sentence pairs: bc → xy and b → y. The translation of a two-word English sentence “b c” into the French sentence “x y” has two possible alignments, and including the one-sentence words, the alignments are:

                         b c   b c   b
                         | |    x    |
                         x y   x y   y

called Parallel, Crossed, and Singleton respectively.

To illustrate an EM algorithm, first set the desired parameter uniformly, that is

t(x | b ) = t(y | b ) = t(x | c ) = t(y | c ) = ¹⁄₂

Then EM iterates as follows

ملف:Em iterations.jpg

Iterations of an EM algorithm

The alignment probability for the “crossing alignment” (where b connects to y) got a boost from the second sentence pair b/y. That further solidified t(y | b), but as a side effect also boosted t(x | c), because x connects to c in that same “crossing alignment.” The effect of boosting t(x | c) necessarily means downgrading t(y | c) because they sum to one. So, even though y and c co-occur, analysis reveals that they are not translations of each other. With real data, EM also is subject to the usual local extremum traps.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

HMMs for speech recognition

ملف:Ski recording.jpg

Vibrational breakdown of "ski"

For decades, speech recognition seemed to hit an impasse as scientists sought descriptive and analytic solution. The sound wave p(t) below is produced by speaking the word “ski”.

انظر أيضاً

وصلات خارجية

هذه بذرة مقالة عن الرياضيات تحتاج للنمو والتحسين، ساهم في إثرائها بالمشاركة في تحريرها.

الكلمات الدالة: