قطع مكافئ
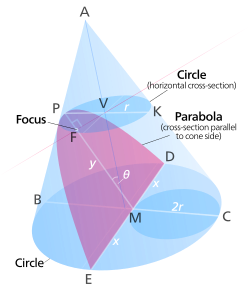
القطع المكافئ Parabola (ويقال له الشلجم والصواب الشلجمي أي ذو شكل الشلجم) هو شكل ثنائي الأبعاد و هو قطع مخروطي، ينشأ من قَطْع سطح مخروطي دائري قائم بمستو موازٍ لراسم هذا السطح (أي الخط المولد له). بمعلومية نقطة (البؤرة) "Focus" وخط مستقيم مقابل في المستوى (الدليل) "directrix"، يكون القطع المكافئ هو المحل الهندسي للنقاط الواقعة في هذا المستوى والتي تبعد عن البؤرة بمسافة مساوية لبعدها عن الدليل. الخط العمودي على الدليل ويمر بالبؤرة يسمى "محور التماثل"، ونقطة تقاطع القطع المكافئ مع محور التماثل تسمى رأس القطع المكافئ "vertex". رأس القطع المكافئ هي نقطة تقع عليه يحدث عندها تغير في اتجاه وأطراد الدالة (أي فترات االتزايد والتناقص) ويكون عندها ميل المماس مساويًا للصفر. قد يكون القطع المكافئ مفتوحًا إلى أعلى أو مفتوحًا إلى أسفل أو إلى اليمين أو اليسار.
للقطوع المكافئة أهمية كبيرة وتطبيقات متعددة، بداية من مرايا السيارات ومصابيحها الأمامية إلى تصميم الصواريخ البالستية. كما أن لها استخدامات كثيرة في الفيزياء والهندسة ومجالات أخرى عديدة.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
هندسيا
القطع المكافئ هو مقطع مخروطي ينتج عن قطع المخروط بمستو مماس للمخروط أو مواز لمستو آخر مماس للمخروط .
تاريخ

أقدم من عمل على دراسة القطوع المخروطية، طبقًا لما هو معروف لدينا، هو منانخيموس في القرن الرابع ق.م. فقد أوجد طريقة لحل مسألة مضاعفة المكعب باستخدام القطوع المكافئة، وقد كان من الصعب حل مثل هذه المسألة بإنشاءات الفرجار والمسطرة. أما أبولونيوس فقد اكتشف العديد من خصائص القطوع المخروطية، كما يعود إليه الفضل في تسمية هذا النوع من القطوع بالقطع المكافئ. خاصية البؤرة-الدليل للقطع المكافئ، يعود الفضل فيها إلى پاپوس السكندري.
أوضح جاليليو أن المقذوفات تتخذ مسارًا على هيئة قطع مكافئ؛ ذلك نتيجة انتظام عجلة الجاذبية الأرضية.
قبل اختراع التليسكوب العاكس كانت فكرة تكون صورة من خلال مرآة القطع المكافئ؛ معروفة. في النصف الأول من القرن السابع عشر اقترح مجموعة من علماء الرياضيات، أمثال رينيه ديكارت ومارين مارسين وجيمس جريجوري، تصميمات لمرايا القطع المكافئ. لكن إسحاق نيوتن تحاشى استخدام هذا النوع من المرايا عندما قام ببناء أول تلسكوب عاكس عام 1668م، وذلك لصعوبة تصنيعها مقارنة بالمرايا الكرية. في الوقت الراهن تستخدم عواكس القطع المكافئ في أغلب التلسكوبات العاكسة الحديثة ، وفي التلسكوبات الفضائية ، وأطباق الاستقبال التلفازي المعدنية، وأطباق اتصالات الساتل الصناعية ، ومستقبلات الرادار.
المعادلة في الإحداثيات الديكارتية
إذا افترضنا أن دليل القطع المكافئ هو الخط x = −p، وأن بؤرته هي النقطة (p, 0). وإذا كانت (x, y) نقطة تنتمي للقطع المكافئ وأنها، من تعريف بابوس للقطع المكافئ، تبعد عن البؤرة مسافة مساوية لبعدها عن الدليل، هذا يعني أن:
بتربيع طرفي المعادلة وبعد التبسيط نحصل على
وهي معادلة القطع الكافئ في صورة من أبسط صوره، ويلاحظ أن محور هذا القطع أفقي. ولتعميم هذه المعادلة نتخيل أن القطع المكافئ أزيح بحيث يكون رأسه هو النقطة (h, k)، بالتالي تصير معادلته
بتبديل الإحداثيات x و y نحصل على المعادلة المقابلة للقطع المكافئ رأسي المحور
المعادلة الأخيرة يمكن كتابتها على الصورة
وبالتالي فإن أي دالة في x إذا كانت كثيرة حدود من الدرجة الثانية فهي قطع مكافئ ذو محور رأسي.
وللتعميم أكثر نقول أن القطع المكافئ هو منحن في المستوى الديكارتي يُعرف بالمعادلة غير القابلة للاختزال والتي على الصورة:
بحيث أن
حيث كل المعاملات حقيقية، وكل من A و B لا يساويان الصفر، ويوجد أكثر من حل وحيد، بحيت تكون مجموعة الحل أزاوج مرتبة على الصورة (x, y)، وهي جميع النقاط الواقعة على المنحنى. كما أن المعادلة غير قابلة للاختزال، بمعنى أنه لا يمكن تحليلها إلى حاصل ضرب معادلتين لا يُشترط أن تكونا خطيتين.
تعريفات هندسية أخرى

القطع المكافئ يمكن تعريفه باعتباره قطع مخروطي اختلافه المركزي يساوي الواحد الصحيح؛ نتيجة لذلك تكون كل القطوع المكافئة متشابهة، بمعنى أن لها نفس الشكل مهما تغير حجمها. ويعتبر القطع المكافئ أيضا نهاية قطوع ناقصة متتابعة، إحدى بؤرتيهم ثابتة والأخرى حرة لتتحرك بعيدًا في اتجاه واحد، بهذا المنطق يمكن النظر إلى القطع المكافئ باعتباره قطع ناقص إحدى بؤرتيه تقع عند ما لا نهاية. القطع المكافئ هو أيضًا تحول عكسي للمنحنى القلبي.
للقطع المكافئ محور تماثل عاكس وحيد، يمر ببؤرته ويتعامد على دليله، ونقطة تقاطع هذا المحور مع القطع المكافئ تدعى رأس القطع المكافئ. دوران القطع المكافئ حول محوره في الإحداثيات ثلاثية الأبعاد يولد شكلًا يعرف بالسطح المكافئي الدوراني.
معادلات
إحداثيات ديكارتية
محور تماثل رأسي
حيث
- .
الصورة البارمترية:
محور تماثل أفقي
حيث
- .
الصورة البارمترية:
قطع مكافئ عام
الصورة العامة للقطع المكافئ هي
هذه النتيجة مشتقة من المعادلة المخروطية العامة المذكور بأعلى:
وبما أنه للقطع المكافئ يكون
- .
معادلة القطع المكافئ العام الذي بؤرته (F(u, v ودليله على الصورة
هي
الوتر البؤري العمودي والإحداثيات القطبية
في الإحداثيات القطبية، القطع المكافئ الذي بؤرته في نقطة الأصل ودليله موازٍ لمحور الصادات تكون معادلته
حيث l هو نصف الوتر البؤري العمودي semilatus rectum (المسافة من البؤرة إلى القطع المكافئ مقاسة عبر خط عمودي على محور تماثله). لاحظ أن هذا مساوٍ لضعف المسافة من البؤرة إلى رأس القطع المكافئ أو المسافة العمودية من رأس المنحنى إلى الوتر البؤري العمودي latus rectum.
الوتر البؤري العمودي هو الوتر المار بالبؤرة وفي نفس الوقت يتعامد على المحور وطوله يساوي 2l.
رأس القطع المكافئ
الإحداثي السيني لرأس القطع المكافئ هو ، ويمكن الحصول عليه عن طريق اشتقاق المعادلة الأصلية للقطع ، وبوضع قيمة المشتقة بصفر (لأن رأس القطع المكافئ هو نقطة حرجة؛ بمعنى أن ميل المماس عنده مساوٍ للصفر)، بحل المعادلة نحصل على الإحداثي السيني لرأس المنحنى، أما الإحداثي الصادي فيمكن الحصلول عليه بالتعويض بقيمة الإحداثي السيني في المعادلة الأصلية كالتالي:
وبالتبسيط:
وبالتالي نقطة رأس القطع المكافئ هي
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
اشتقاق إحداثيات البؤرة ومعادلة الدليل
لتحديد إحداثيات النقطة البؤرية لقطع مكافئ بسيط ذي محور تماثل موازٍ لمحور الصادات (محور تماثل رأسي)، ورأسه يقع عند نقطة الأصل (0,0)، ولتكن معادلته على الصورة:
فإن أي نقطة على القطع المكافئ ستقع على مسافة من النقطة البؤرية (0,f) مساوية للمسافة بينها وبين الدليل L، الذي يتعامد على محور تماثل القطع المكافئ (في هذه الحالة يوزاي محور السينات)، ويمر بالنقطة (0,f-)، وبالتالي فإن أي نقطة (P=(x,y على القطع المكافئ ستكون على مسافة متساوية من كلتا النقطتين (0,f) و (x,-f).
أي خط FP يصل بين البؤرة وأي نقطة على القطع المكافئ يتساوى في الطول مع أي خط QP مرسوم عموديًا من هذه النقطة الواقعة على القطع المكافئ إلى الدليل ويقطعه في النقطة Q.
المثلث القائم الذي وتره FP، وطولا ضلعي قائمته هما: x و f-y (المسافة الرأسية بين F و P)، يكون طول وتره
(لاحظ أن ²(f-y) و²(y-f) يعطيان نفس الناتج لأنهما مربعان.)
طول الخط QP يساوي المسافة الرأسية بين النقطة P ومحور السينات (أي المسافة y) بالإضافة إلى المسافة الرأسية من محور السينات إلى الدليل (أي المسافة f).
هاتان القطعتان المستقيمتان متساويتان في الطول، وكما ذكر سابقًا y=ax² وبالتالي
بتربيع الطرفين
بطرح الحدود المتشابهة من الطرفين
بقسمة x² من الطرفين (بفرض أن x لا تساوي الصفر)
وبالتالي للقطع المكافئ الذي على الصورة f(x)=x²، المعامل a يساوي 1، وبالتالي فإن النقطة البؤرية F هي (0,¼)
كما ذكر أعلاه، هذا هو اشتقاق النقطة البؤرية لقطع مكافئ بسيط، رأسه في نقطة الأصل ويتماثل حول محور الصادات، أما بالنسبة لأي قطع مكافئ معمم، معادلته على الصورة القياسية
- ,
بؤرته تقع عند النقطة
والتي يمكن كتابتها على الصورة
والدليل يعطى بالعلاقة
والتي يمكن أن تكتب على الصورة
قطع مخروطي وشكل من الدرجة الثانية
المخطط والوصف والتعريفات
أمثلة لمعادلات قطع مكافئ رأسه ( 0 ، 0 )
ص تربيع = 4×أس( فتحته يمين اتجاه س + )ومعادلة دليله س = -أ
ص تربيع = - 4 × أس ( فتحته يسار اتجاه س - )ومعادلة دليله س = أ
س تربيع = 4×أ ص ( فتحته أعلى اتجاه ص + )ومعادلة دليله ص = -أ
س تربيع = - 4 × أص ( فتحته تحت اتجاه ص - )ومعادلة دليله ص= أ
مرايا مرصد كيك
مرصد كيك الفلكي في هاواي ينكون من مرصدين ، كل منهما مزود بمرآة مقعرة في شكل قطع زائد . معظم التلسكوبات الحديثة تعمل بمرايا في شكل القطع المكافيء ، ويصل قطر بعضها نحو 8 متر.وهي تعمل على تجميع قدر كبير من الضوء وتصور أجراما كونية قريبة وبعيدة . تمكن الإنسان من اكتشاف أجراما صغيرة جدا ,اجراما بعيدة جدا ، وبفضل تلك الأجهزة الدقيقة تعرف الإنسان الحديث على أشياء كثيرة في الكون .
كذلك يعمل تلسكوب هابل الفضائي بمرايا مقعرة بشكل القطع المكافيء.
كما تشكل أطباق استقبال التلفاز في شكل قطع مكافيء لاستقبال وتركيز أمواج التلفزة في بؤرة تضخم الإشارات .
لا تصلح مرآة كرية (جزء من الكرة) كمرآة لتلسكوب حيث أنها تكون عدة بؤر خلف بعضها البعض ، ولا تجمع الأشعة في بؤرة واحدة. تلك الظاهرة تسمى إزاغة كرية ونتيجتها تكوين صورة غير واضحة.
معرض
Click on any image to enlarge it.
A bouncing ball captured with a stroboscopic flash at 25 images per second. Note that the ball becomes significantly non-spherical after each bounce, especially after the first. That, along with spin and air resistance, causes the curve swept out to deviate slightly from the expected perfect parabola.
The path (in red) of Comet Kohoutek as it passed through the inner solar system, showing its nearly parabolic shape. The blue orbit is the Earth's
The supporting cables of suspension bridges follow a curve which is intermediate between a parabola and a catenary.
The Rainbow Bridge across the Niagara River, connecting Canada (left) to the الولايات المتحدة (right). The parabolic arch is in compression, and carries the weight of the road.
Parabolic shape formed by a liquid surface under rotation. Two liquids of different densities completely fill a narrow space between two sheets of transparent plastic. The gap between the sheets is closed at the bottom, sides and top. The whole assembly is rotating around a vertical axis passing through the centre. (See Rotating furnace)
Parabolic microphone with optically transparent plastic reflector, used to overhear referee conversations at an American college football game.
Array of parabolic troughs to collect solar energy
Edison's searchlight, mounted on a cart. The light had a parabolic reflector.
Physicist Stephen Hawking in an aircraft flying a parabolic trajectory to simulate zero-gravity
معرض مخططات
Click on any image to enlarge it. To shrink back, return to previous page.
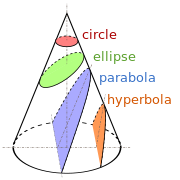
The parabola is a member of the family of conic sections.
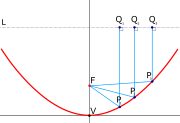
Parabolic curve showing directrix (L) and focus (F). The distance from any point on the parabola to the focus (PnF) equals the perpendicular distance from the same point on the parabola to the directrix (PnQn).
اقرأ أيضا
- Catenary
- سطح مكافئ
- قطع ناقص
- قطع زائد
- مرآة قكع مكافيء
- Parabolic dome
- Parabolic partial differential equation
- Parabolic reflector
- Paraboloid
- Quadratic equation
- Quadratic function
- Rotating furnace, paraboloids produced by rotation
- Rotation of axes
- Translation of axes
- Universal parabolic constant
الهامش
ملاحظات
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
وصلات خارجية
- Hazewinkel, Michiel, ed. (2001), "Parabola", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
- Eric W. Weisstein, Parabola at MathWorld.
- Interactive parabola-drag focus, see axis of symmetry, directrix, standard and vertex forms
- Archimedes Triangle and Squaring of Parabola at cut-the-knot
- Two Tangents to Parabola at cut-the-knot
- Parabola As Envelope of Straight Lines at cut-the-knot
- Parabolic Mirror at cut-the-knot
- Three Parabola Tangents at cut-the-knot
- Module for the Tangent Parabola
- Focal Properties of Parabola at cut-the-knot
- Parabola As Envelope II at cut-the-knot
- The similarity of parabola at Dynamic Geometry Sketches, interactive dynamic geometry sketch.