شبكات عصبونية

حنان كبريته ساهم بشكل رئيسي في تحرير هذا المقال

Simplified view of a feedforward artificial neural network

الشبكات العصبونية Neural network، مجموعة مترابطة من العصبونات البيولوجية أو العصبونات الاصطناعية لذلك يمكننا الحديث عن :

• شبكات عصبونية بيولوجية: تمثلها الدماغ أو أي جزء منه .
• شبكات عصبونية اصطناعية: و هي عبارة عن نماذج حاسوبية ، أو ميكانيكية أو الكترونية تقوم بمحاكاة عمل العصبونات و اتصالاتها . لكن هذه الشبكات الاصطناعية قد تطورت و تنوعت طرق عملها بحيث نشأت منها بعض النواع لا تشابه بأي حال طريقة عمل أي شبكة بيولوجية .

الشبكات العصبونية الاصطناعية هي من أهم المواضيع التي تعالجها المعلوماتية العصبونية ولها دور كبير في مجالات الذكاء الإصطناعي وهي طريقة يحاول فيها العلماء محاكاة Simulation عملية معالجة المعلومات في الدماغ البشري. كما أن المشابك العصبونية أيضا مناسبة لدراسة بعض الظواهر الدماغية خاصة من الناحية المعلوماتية لذلك فإن نجاحات هذا المجال العلمي متصلة بشكل وثيق بالنجاحات في مجال النيوروبيولوجيا.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 التاريخ

المقالة الرئيسية: Connectionism

قاد علم العصبونات الباحثين إلى بناء نماذج رياضية تحاكي سلوك العصبونات متمثلةً بالشبكات العصبونية الصناعية. تعود هذه الفكرة إلى عام 1940 عندما قَدَّم ماكولوش McCulloch وبيتس Pitts أول نموذج تجريدي للخلية العصبية. وقد وضع هيب Hebb قانون التعلّم Learning law في عام 1949، شرح فيه كيفية تعلّم الخلايا العصبية. ووضع روسنبلات Rosenblat في عام 1950 خوارزمية تعلم البيرسبترون Perceptron.

طور كونن Kohonen عام 1977 نماذج الذاكرة المترابطة، وطبق هوبفيلد Hopfield عام 1982 فكرة تصغير الطاقة في الفيزياء على الشبكات العصبونية. وقدم هينتون Hinton وسيجنوسكي Sejnowski وآكلي Ackley في المدة 1983ـ1984 آلة بولتزمان Boltzman.

وضعت خوارزمية الانتشار التراجعي Back Propagation في عامي 1985 و1986، مما فتح المجال واسعاً أمام البيرسبترون متعدّد الطبقات Multi Layer Perceptron نحومزيد من التطور. وقد أدى هذا التطور إلى استخدام مفهوم الشبكات العصبونية في العديد من المجالات المتقدمة.

 مبدأ عمل الشبكات العصبونية الصناعية

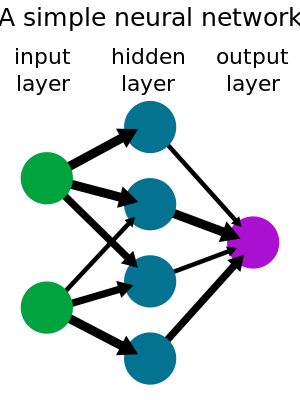
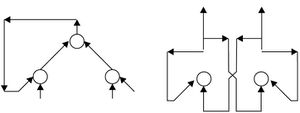
تستقبل العصبونات مداخل تناظر النبضات الكهروكيمياوية التي تستقبلها النهايات العصبية في الخلية الطبيعية، وتناظر مخارج العصبون الصنعي الإشارات الخارجة من الخلية الطبيعية عن طريق المحور العصبي، فتؤدي بعض المداخل إلى تحريض العصبون وأخرى تميل إلى إخماده. وعندما يتجاوز تراكم التأثير مستوى العتبة، يتحرَّض العصبون ويرسل إشارات إلى عصبونات أخرى فيتحدد مستوى التحريض بمجموع المداخل المثقّلة حسب العلاقة: (الشكل 1)

(الشكل 1)

تُمثَل الشبكة العصبونية كما هو مبين في الشكل رقم (1) بمجموعة عقد وارتباطات، وتشير العقدة إلى العصبون بينما تشير الأسهم إلى الارتباطات التي تمر عبرها الإشارات بين العصبونات.

تحل الشبكات العصبونية المشكلات بالتعلّم الذاتي والتنظيم الذاتي، وتستمد ذكاءها من سلوك ارتباط الوحدات الحسابية البسيطة في عصبونات متعددة.

معالجة المعلومات العصبية

 المخ، الشبكات العصبية والحواسب

 الشبكات العصبونية والذكاء الصناعي

المقالة الرئيسية: شبكات عصبونية اصطناعية

 خصائص الشبكات العصبونية الصنعية

يتطلب بناء الشبكة العصبونية الصنعية تحديد طوبولوجيا الشبكة وخصائص العقد،وتحديد ديناميكية المنظومة.

 طوبولوجيا الشبكة

تشير طوبولوجيا الشبكة إلى الإطار العام لمخطط الارتباط الداخلي الذي يُحدّد بعدد الطبقات وعدد العقد في الطبقة الواحدة، توجد عادة في الشبكات العصبونية طبقات ثلاث هي: طبقة الدخل، والطبقة المخفية، وطبقة الخرج.

تُصنّف الشبكات العصبونية وفقاً لمخطط الارتباط الداخلي في:

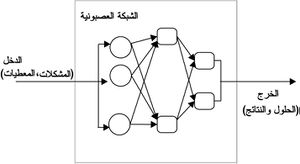
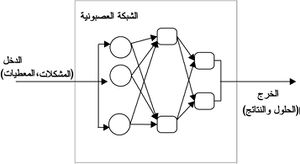
• ـ شبكات تغذية أمامية: يكون لارتباطاتها الاتجاه نفسه من وحدات الدخل إلى وحدات الخرج. ويبين الشكل رقم (2) أمثلة على شبكات تغذية أمامية.

الشكل (2) أمثلة على شبكات تغذية أمامية

الشكل (3) أمثلة على شبكات عودية

كما يمكن أن تكون الارتباطات في الشبكة العصبونية متناظرة أو غير متناظرة، إلا أن جميع هذه الارتباطات توزّن بعوامل weight factors يمكن ضبطها في أثناء تعلّم الشبكة.

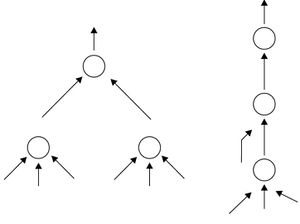
• ـ شبكات عودية: تحتوي على ارتباطات راجعة أو حلقات. ويبين الشكل رقم (3) أمثلة على شبكات عودية.

 خصائص العقد

الشكل (4)

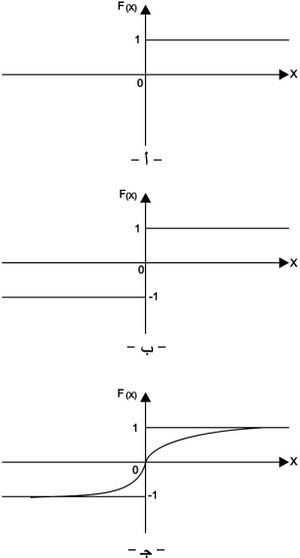
تكون مستويات تحريض العقد إما قيماً متقطعة وإما قيماً مستمرة، ويعتمد ذلك على تابع التحويل المختار. فتأخذ مثلاً مستويات التحريض في حالة تابع الحد الفاصل Hard-Limiting شكل (4 ـ أ) إحدى القيمتين إما 0 أو1، وفي تابع التحويل (الإشارة) Sign Function (الشكل 4 ـ ب) إحدى القيمتين إما 1 و-1، وفي تابع التحويل Sigmoid Function (الشكل 4 ـ ج) مجالاً مستمراً [0,1] وفقاً للعلاقة الآتية:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 دينامية المنظومة

تتحقق دينامية الشبكات العصبونية بقدرتها على التعلّم،وذلك بتعديل أوزان ارتباطاتها الداخلية. وتتعلم أغلب الشبكات بنوعين من أنواع خوارزميات التعلّم هي:

• التعلّم المراقب: تضبط قوة الارتباطات الداخلية ووزنها بحسب الفرق بين مخارج الشبكة المطلوبة التي تحدد من قبل المراقب،والمخارج الفعلية من أجل دخل معين.

• التعلّم غير المراقب: لا تتطلب هذه الخوارزميات مخارج هدف. تُقدم نماذج دخل إلى الشبكة العصبونية التي تقوم بضبط أوزان ارتباطاتها آلياً لتجميع نماذج الدخل في مجموعات حسب تشابهها.

د ـ أنواع الشبكات العصبونية:

يمكن تصنيف الشبكات العصبونية في النماذج الآتية:

نماذج التصنيف: تستخدم لتصنيف معطيات الدخل في صنف من عدد محدد من الأصناف، يدخل ضمن هذا النوع من النماذج الشبكات الآتية: البيرسبترون وحيد الطبقة Single-Layer Perceptron، والبيرسبترون متعدد الطبقات Multi-layer Perceptron،والعنصر الموائم الخطي Adaptive Linear Element.

نماذج الترابط: تستخدم من أجل استرجاع عنصر ما اعتماداً على جزء من العنصر نفسه أوباستخدام عنصر آخر. يدخل ضمن هذه النماذج شبكات هوبفيلد Hopfield Networks والذواكر المترابطة Associative Memories.

نماذج الأمثَلة: من أجل إيجاد أفضل الحلول الممكنة لمسألة ما، وذلك تحت شروط معينة. ومن الشبكات العصبونية المستخدمة في تطبيقات نماذج الأمثلة: شبكات هوبفيلد، وآلات بولتزمان Boltzmann machines.

نماذج الترتيب الذاتي: ترتب المعطيات المدخلة باستخدام قدرات التعلم التنافسي، ويدخل ضمنها شبكات كونن Kohonen Networks.

هـ ـ تطبيقات الشبكات العصبونية:

للشبكات العصبونية تطبيقات فعالة وجيدة في مجالات هندسية وعلمية كثيرة، وخاصةً عند التعامل مع حجم كبير من المعطيات منها:

• ـ اكتساب المعارف.

• ـ معالجة اللغات الطبيعية.

• ـ التعرف على المحارف.

• ـ ضغط الصور.

• ـ التنبؤات المالية: مثل التنبؤ بسوق البورصة.

• ـ تطبيقات طبية : مثل التشخيص الطبي.

• ـ المنظومات المساعدة في اتخاذ القرار.

• ـ معالجة الإشارة والرؤية الآلية والروبوتية.

• ـ التحكم والأتمتة.

و ـ الآفاق المستقبلية:

يسعى الباحثون في مجال الشبكات العصبونية الصنعية أن تصل هذه الشبكات في المستقبل إلى محاكاة كاملة للدماغ الإنساني وأن تصبح الآلة تحس وتشعر. ولا يقتصر مستقبل الشبكات العصبونية على ذلك، وإنما يطمح إلى تحقيق أهداف مهمة لتطوير المنظومات المعتمدة على الشبكات العصبونية وفقاً لما يأتي:

1ـ مكاملة المنطق العائم مع الشبكات العصبونية.

2ـ تطوير الشبكات العصبونية النبضية.

3ـ تطوير الشبكات العصبونية العتادية.

4ـ تطوير تقنيات الشبكات العصبونية الموجودة لتمكنها في المستقبل أن تسمح بروبوت يمكنه أن يرى ويحس ويتنبأ بالعالم المحيط، والتنبؤ بسوق البورصة، وعزف الموسيقى، والتحويل الآلي للوثائق المكتوبة بخط اليد إلى وثائق بتنسيق معالج الكلمات،والتشخيص الطبي الذاتي، وأكثر من ذلك.

 انظر أيضا

• ADALINE
• Adaptive resonance theory
• Biological cybernetics
• Biologically inspired computing
• Cerebellar model articulation controller
• Cognitive architecture
• Cognitive science
• Connectomics
• Cultured neuronal networks
• Deep learning
• Deep Image Prior
• Digital morphogenesis
• Efficiently updatable neural network
• Exclusive or
• Gene expression programming
• Generative adversarial network
• Group method of data handling
• Habituation
• In situ adaptive tabulation
• Memristor
• Multilinear subspace learning
• Neural network software
• Nonlinear system identification
• Parallel constraint satisfaction processes
• Parallel distributed processing
• Predictive analytics
• Radial basis function network
• Self-organizing map
• Simulated reality
• Support vector machine
• Tensor product network
• Time delay neural network

 المصادر

• الموسوعة العربية

 قراءات إضافية

• Arbib, Michael A. (Ed.) (1995). The Handbook of Brain Theory and Neural Networks.
• Alspector, U.S. Patent 4٬874٬963 "Neuromorphic learning networks". October 17, 1989.
• Agre, Philip E. (1997). Computation and Human Experience. Cambridge University Press. ISBN 0-521-38603-9., p. 80
• Yaneer Bar-Yam (2003). Dynamics of Complex Systems, Chapter 2. {{cite book}}: External link in |title= (help)
• Yaneer Bar-Yam (2003). Dynamics of Complex Systems, Chapter 3. {{cite book}}: External link in |title= (help)
• Yaneer Bar-Yam (2005). Making Things Work. {{cite book}}: External link in |title= (help) See chapter 3.
• Bertsekas, Dimitri P. (1999). Nonlinear Programming.
• Bertsekas, Dimitri P. & Tsitsiklis, John N. (1996). Neuro-dynamic Programming.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Bhadeshia H. K. D. H. (1992). "Neural Networks in Materials Science". ISIJ International. 39: 966–979. doi:10.2355/isijinternational.39.966. {{cite journal}}: External link in |title= (help)
• Boyd, Stephen & Vandenberghe, Lieven (2004). Convex Optimization. {{cite book}}: External link in |title= (help)CS1 maint: multiple names: authors list (link)
• Dewdney, A. K. (1997). Yes, We Have No Neutrons: An Eye-Opening Tour through the Twists and Turns of Bad Science. Wiley, 192 pp. See chapter 5.
• Egmont-Petersen, M., de Ridder, D., Handels, H. (2002). "Image processing with neural networks - a review". Pattern Recognition. 35 (10): 2279–2301. doi:10.1016/S0031-3203(01)00178-9.{{cite journal}}: CS1 maint: multiple names: authors list (link)
• Fukushima, K. (1975). "Cognitron: A Self-Organizing Multilayered Neural Network". Biological Cybernetics. 20: 121–136. doi:10.1007/BF00342633.
• Frank, Michael J. (2005). "Dynamic Dopamine Modulation in the Basal Ganglia: A Neurocomputational Account of Cognitive Deficits in Medicated and Non-medicated Parkinsonism". Journal of Cognitive Neuroscience. 17 (1): 51–72. doi:10.1162/0898929052880093. PMID 15701239.
• Gardner, E.J., & Derrida, B. (1988). "Optimal storage properties of neural network models". Journal of Physics a. 21: 271–284. doi:10.1088/0305-4470/21/1/031.{{cite journal}}: CS1 maint: multiple names: authors list (link)
• Hadzibeganovic, Tarik & Cannas, Sergio A. (2009). "A Tsallis' statistics based neural network model for novel word learning". Physica A: Statistical Mechanics and its Applications. 388(5): 732–746.{{cite journal}}: CS1 maint: multiple names: authors list (link)
• Krauth, W., & Mezard, M. (1989). "Storage capacity of memory with binary couplings". Journal de Physique. 50: 3057–3066. doi:10.1051/jphys:0198900500200305700.{{cite journal}}: CS1 maint: multiple names: authors list (link)
• Maass, W., & Markram, H. (2002). "On the computational power of recurrent circuits of spiking neurons". Journal of Computer and System Sciences. 69(4): 593–616. {{cite journal}}: External link in |title= (help)CS1 maint: multiple names: authors list (link)
• MacKay, David (2003). Information Theory, Inference, and Learning Algorithms. {{cite book}}: External link in |title= (help)
• Mandic, D. & Chambers, J. (2001). Recurrent Neural Networks for Prediction: Architectures, Learning algorithms and Stability. Wiley.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Minsky, M. & Papert, S. (1969). An Introduction to Computational Geometry. MIT Press.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Muller, P. & Insua, D.R. (1995). "Issues in Bayesian Analysis of Neural Network Models". Neural Computation. 10: 571–592.{{cite journal}}: CS1 maint: multiple names: authors list (link)
• Reilly, D.L., Cooper, L.N. & Elbaum, C. (1982). "A Neural Model for Category Learning". Biological Cybernetics. 45: 35–41. doi:10.1007/BF00387211.{{cite journal}}: CS1 maint: multiple names: authors list (link)
• Rosenblatt, F. (1962). Principles of Neurodynamics. Spartan Books.
• Sun, R. & Bookman,L. (eds.) (1994.). Computational Architectures Integrating Neural and Symbolic Processes. Kluwer Academic Publishers, Needham, MA. {{cite book}}: |author= has generic name (help); Check date values in: |year= (help)CS1 maint: multiple names: authors list (link)
• Sutton, Richard S. & Barto, Andrew G. (1998). Reinforcement Learning : An introduction. {{cite book}}: External link in |title= (help)CS1 maint: multiple names: authors list (link)
• Van den Bergh, F. Engelbrecht, AP. "Cooperative Learning in Neural Networks using Particle Swarm Optimizers". CIRG 2000.
• Wilkes, A.L. & Wade, N.J. (1997). "Bain on Neural Networks". Brain and Cognition. 33 (3): 295–305. doi:10.1006/brcg.1997.0869. PMID 9126397.{{cite journal}}: CS1 maint: multiple names: authors list (link)
• Wasserman, P.D. (1989). Neural computing theory and practice. Van Nostrand Reinhold.
• Jeffrey T. Spooner, Manfredi Maggiore, Raul Ord onez, and Kevin M. Passino, Stable Adaptive Control and Estimation for Nonlinear Systems: Neural and Fuzzy Approximator Techniques, John Wiley and Sons, NY, 2002.
• Peter Dayan, L.F. Abbott. Theoretical Neuroscience. MIT Press.
• Wulfram Gerstner, Werner Kistler. Spiking Neuron Models:Single Neurons, Populations, Plasticity. Cambridge University Press.
• Steeb, W-H (2008). The Nonlinear Workbook: Chaos, Fractals, Neural Networks, Genetic Algorithms, Gene Expression Programming, Support Vector Machine, Wavelets, Hidden Markov Models, Fuzzy Logic with C++, Java and SymbolicC++ Programs: 4th edition. World Scientific Publishing. ISBN 981-281-852-9.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 وصلات خارجية

• LearnArtificialNeuralNetworks - Robot control and neural networks
• Review of Neural Networks in Materials Science
• Artificial Neural Networks Tutorial in three languages (Univ. Politécnica de Madrid)
• Introduction to Neural Networks and Knowledge Modeling
• Another introduction to ANN
• Next Generation of Neural Networks - Google Tech Talks
• Performance of Neural Networks
• Neural Networks and Information
• PMML Representation - Standard way to represent neural networks