حدسية كپلر
في الرياضيات، حدسية كپلر Kepler conjecture هي حدسية حول تعبئة الكرات في الفضاء الإقليدي. تنص هذه الحدسية على أن لايوجد أي ترتيب لتعبئة كرات متساوية الحجم يكون ذو كثافة أكبر من كثافة التعبئة المتراصة في شكل هرم مسدس HCP، حيث تكون هذه الكثافة تساوي حوالي 74%.
شرح الحدسية
تخيل ملء علبة كبيرة بكمية من الكرات الصغيرة. كلما زادت كثافة الكرات داخل العلبة كلما زاد عدد الكرات الممكن وضعها داخل العلبة، حيث أن الكثافة متناسبة مع الحجم الذي تشغله الكرات داخل العلبة. حتى نحصل على أكبر عدد للكرات في العلبة هناك حاجة لإيجاد ترتيب يعطي أكبر كثافة، بحيث تكون الكرات متراصة إلى بعضها البعض بأكبر درجة ممكنة.
توضح التجارب أن إسقاط الكرات بعشوائية سيعطي كثافة حوالي 65%. بينما من الممكن الحصول على كثافة عالية عن طريق ترتيب الكرات على النحو التالي:
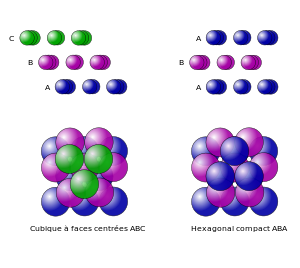
- ابدأ بطبقة من الكرات تشكل مسدس
- الكرة التالية في الصف التالي توضع في أسفل نقطة فوق الطبقة الأولى (مثلما ترتب البرتقالات في محلات بيع الفواكة)
- تعطي هذه الطريقة نوعين من الترتيب هما:
- الترتيب المكعبي مركز الأوجه HCC
- الترتيب الموشوري المسدسي HCP
كلا هذين الترتيبين له كثافة وسطية تساوي
وحدسية كيبلر تقول أن هذا الرقم هو أكبر كثافة من الممكن الوصول لها في تعبئة الكرات.
مراجع
وصلات خارجية
- Eric W. Weisstein, Kepler Conjecture at MathWorld.
- Front page of 'On the six-cornered snowflake'
- Thomas Hales' home page
- Flyspeck project home page
- Overview of Hales' proof
- Article in American Scientist by Dana Mackenzie
- Flyspeck I: Tame Graphs, verified enumeration of tame plane graphs as defined by Thomas C. Hales in his proof of the Kepler Conjecture