تعبئة متراصة (رياضيات)

hcp and fcc close-packing of spheres

في الهندسة المتقطعة، التعبئة المتراصة لمجموعة كرات هو عبارة عن ترتيب لكرات ضمن شبكة منتظمة منتهية بحيث تشغل هذه الكرات أصغر حجم ممكن في الفضاء الثلاثي الأبعاد.

{\frac {\pi }{3{\sqrt {2}}}}\simeq 0.74048.

حدسية كپلر تقول أنها أعلى كثافة يمكن تحقيقها بأي ترتيب للكرات، سواء كانت منتظمة أو غير منتظمة. This conjecture is now widely considered proven by T. C. Hales.^[1]^[2]

برهن كارل فريدرش گاوس أن أكبر كثافة وسطية من الممكن أن تصل إليه لتعبئة متراصة ضمن شبكة منتظمة هو ${\frac {\pi }{3{\sqrt {2}}}}\simeq 0.74048$ . كما تنص حدسية كپلر أنه يتم الوصول إلى النسبة العظمى للكثافة بتعبئة متراصة لكرات ضمن شبكة منتظمة أو غير منتظمة.

هناك نوعان من الشبكات التي تمكن من الوصول لأعلى كثافة:

مكعب مركزي الوجوه FCC
تعبئة متراصة موشور مسدس HCP.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

مشكلة القنابل

Cannonballs piled on a triangular (front) and rectangular (back) base

{\text{pitch}}_{Z}={\sqrt {6}}\cdot {d \over 3}\approx 0.81649658d,

مقارنة بين hcp و fcc

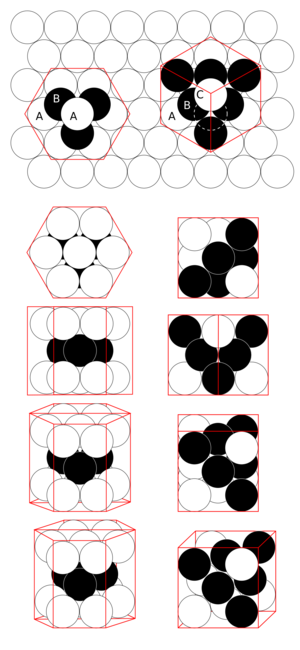
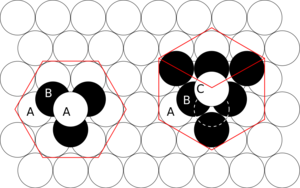
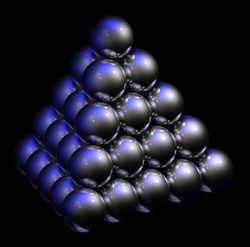
Figure 1 – The hcp lattice (left) and the fcc lattice (right). The outline of each respective Bravais lattice is shown in red. The letters indicate which layers are the same. There are two "A" layers in the hcp matrix, where all the spheres are in the same position. All three layers in the fcc stack are different. Note the fcc stacking may be converted to the hcp stacking by translation of the upper-most sphere, as shown by the dashed outline.	Figure 2 – Thomas Harriot, circa 1585, first pondered the mathematics of the cannonball arrangement or cannonball stack, which has an fcc lattice. Note how adjacent balls along each edge of the regular tetrahedron enclosing the stack are all in direct contact with one another. This does not occur in an hcp lattice, as shown in Fig. 3.	Figure 3 – Shown here is a stack of eleven spheres of the hcp lattice illustrated in Fig. 1. The hcp stack differs from the top 3 tiers of the fcc stack shown in Fig. 2 only in the lowest tier; it can be modified to fcc by an appropriate rotation or translation.

توليد العقود

Simple hcp lattice

ملف:Animated-HCP-Lattice.gif

An animation of hcp lattice generation.

مؤشرات ميلر

Miller-Bravais index for hcp lattice

انظر أيضاً

الهامش

^ Hales, T. C. (1998). "An overview of the Kepler conjecture". Arxiv preprint math. {{cite journal}}: Cite journal requires |journal= (help)
^ "Mathematics: Does the proof stack up?".