متتالية حسابية

Visual proof of the derivation of arithmetic progression formulas – the faded blocks are a rotated copy of the arithmetic progression

المتتالية الحسابية في الرياضيات هي متتالية من الأعداد بحيث يكون الفرق بين أي عددين متتالين ثابتا. على سبيل المثال فإن 3, 5, 7, 9, 11, 13, … هي متتالية حسابية لها أساس يساوي 2.

تتميز المتتاليات بصفة "التقطع" الناجمة عن ارتباط المتتاليات بالأعداد الطبيعية التي يدركها فكرنا أكثر مما يدرك الأعداد الأخرى كالأعداد الحقيقية أو المركبة (العقدية). والدليل على ذلك ظهور واستخدام الأعداد الطبيعية قبل سائر أنماط الأعداد الأخرى.

إذا كان الحد الأول من المتتالية الحسابية هو $a_{1}$ والفرق بين حدين متتاليين هو $d$ عندها يعبر عن الحد ذو الترتيب $n$ من متتالية حسابية بالعلاقة التالية:

$\ a_{n}=a_{1}+(n-1)d,$

أو بشكل عام

$\ a_{n}=a_{m}+(n-m)d.$

$\ a_{n}=a_{m}+(n-m)d$.

A finite portion of an arithmetic progression is called a finite arithmetic progression and sometimes just called an arithmetic progression. The sum of a finite arithmetic progression is called an arithmetic series.

The behavior of the arithmetic progression depends on the common difference d. If the common difference is:

• positive, then the members (terms) will grow towards positive infinity;
• negative, then the members (terms) will grow towards negative infinity.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الجمع

2	+	5	+	8	+	11	+	14	=	40
14	+	11	+	8	+	5	+	2	=	40
16	+	16	+	16	+	16	+	16	=	80

Computation of the sum 2 + 5 + 8 + 11 + 14. When the sequence is reversed and added to itself term by term, the resulting sequence has a single repeated value in it, equal to the sum of the first and last numbers (2 + 14 = 16). Thus 16 × 5 = 80 is twice the sum.

The sum of the members of a finite arithmetic progression is called an arithmetic series. For example, consider the sum:

$2+5+8+11+14$

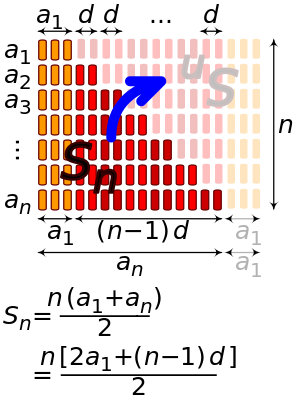
This sum can be found quickly by taking the number n of terms being added (here 5), multiplying by the sum of the first and last number in the progression (here 2 + 14 = 16), and dividing by 2:

${\frac {n(a_{1}+a_{n})}{2}}$

In the case above, this gives the equation:

$2+5+8+11+14={\frac {5(2+14)}{2}}={\frac {5\times 16}{2}}=40.$

This formula works for any real numbers $a_{1}$ and $a_{n}$. For example:

$\left(-{\frac {3}{2}}\right)+\left(-{\frac {1}{2}}\right)+{\frac {1}{2}}={\frac {3\left(-{\frac {3}{2}}+{\frac {1}{2}}\right)}{2}}=-{\frac {3}{2}}.$

 الاشتقاق

Animated proof for the formula giving the sum of the first integers 1+2+...+n.

To derive the above formula, begin by expressing the arithmetic series in two different ways:

$S_{n}=a_{1}+(a_{1}+d)+(a_{1}+2d)+\cdots +(a_{1}+(n-2)d)+(a_{1}+(n-1)d)$

$S_{n}=(a_{n}-(n-1)d)+(a_{n}-(n-2)d)+\cdots +(a_{n}-2d)+(a_{n}-d)+a_{n}.$

Adding both sides of the two equations, all terms involving d cancel:

$\ 2S_{n}=n(a_{1}+a_{n}).$

Dividing both sides by 2 produces a common form of the equation:

$S_{n}={\frac {n}{2}}(a_{1}+a_{n}).$

An alternate form results from re-inserting the substitution: $a_{n}=a_{1}+(n-1)d$:

$S_{n}={\frac {n}{2}}[2a_{1}+(n-1)d].$

Furthermore, the mean value of the series can be calculated via: $S_{n}/n$:

${\overline {n}}={\frac {a_{1}+a_{n}}{2}}.$

The formula is very similar to the mean of a discrete uniform distribution.

In 499 AD Aryabhata, a prominent mathematician-astronomer from the classical age of Indian mathematics and Indian astronomy, gave this method in the Aryabhatiya (section 2.18).

According to an anecdote, young Carl Friedrich Gauss reinvented this method to compute the sum 1+2+3+...+99+100 for a punishment in primary school.

 حاصل الضرب

The product of the members of a finite arithmetic progression with an initial element a₁, common differences d, and n elements in total is determined in a closed expression

$a_{1}a_{2}\cdots a_{n}=d{\frac {a_{1}}{d}}d\left({\frac {a_{1}}{d}}+1\right)d\left({\frac {a_{1}}{d}}+2\right)\cdots d\left({\frac {a_{1}}{d}}+n-1\right)=d^{n}{\left({\frac {a_{1}}{d}}\right)}^{\overline {n}}=d^{n}{\frac {\Gamma \left(a_{1}/d+n\right)}{\Gamma \left(a_{1}/d\right)}},$

where $x^{\overline {n}}$ denotes the rising factorial and $\Gamma$ denotes the Gamma function. (The formula is not valid when $a_{1}/d$ is a negative integer or zero.)^{[بحاجة لمصدر]}

This is a generalization from the fact that the product of the progression $1\times 2\times \cdots \times n$ is given by the factorial $n!$ and that the product

$m\times (m+1)\times (m+2)\times \cdots \times (n-2)\times (n-1)\times n$

for positive integers $m$ and $n$ is given by

${\frac {n!}{(m-1)!}}.$

Taking the example 3, 8, 13, 18, 23, 28, ..., the product of the terms of the arithmetic progression given by a_n = 3 + (n-1)×5 up to the 50th term is

$P_{50}=5^{50}\cdot {\frac {\Gamma \left(3/5+50\right)}{\Gamma \left(3/5\right)}}\approx 3.78438\times 10^{98}.$

 الحيود المعياري

The standard deviation of any arithmetic progression can be calculated as

$\sigma =|d|{\sqrt {\frac {(n-1)(n+1)}{12}}}$

where $n$ is the number of terms in the progression and $d$ is the common difference between terms. The formula is very similar to the standard deviation of a discrete uniform distribution.

 التقاطعات

The intersection of any two doubly infinite arithmetic progressions is either empty or another arithmetic progression, which can be found using the Chinese remainder theorem. If each pair of progressions in a family of doubly infinite arithmetic progressions have a non-empty intersection, then there exists a number common to all of them; that is, infinite arithmetic progressions form a Helly family. However, the intersection of infinitely many infinite arithmetic progressions might be a single number rather than itself being an infinite progression.

 ملخص الصيغ

If

$a_{1}$ is the first term of an arithmetic progression.

$a_{n}$ is the nth term of an arithmetic progression.

$d$ is the difference between terms of the arithmetic progression.

$n$ is the number of terms in the arithmetic progression.

$S_{n}$ is the sum of n terms in the arithmetic progression.

${\overline {n}}$ is the mean value of arithmetic series.

then

1. $\ a_{n}=a_{1}+(n-1)d,$

2. $\ a_{n}=a_{m}+(n-m)d.$

3. $S_{n}={\frac {n}{2}}[2a_{1}+(n-1)d].$

4. $S_{n}={\frac {n}{2}}(a_{1}+a_{n}).$

5. ${\overline {n}}$ = $S_{n}/n$

6. ${\overline {n}}={\frac {a_{1}+a_{n}}{2}}.$

7. $d={\frac {a_{m}-a_{n}}{m-n}};m\neq n$.

 انظر أيضاً

• Primes in arithmetic progression
• Linear difference equation
• Arithmetico-geometric sequence
• Generalized arithmetic progression, a set of integers constructed as an arithmetic progression is, but allowing several possible differences
• Harmonic progression
• Heronian triangles with sides in arithmetic progression
• Problems involving arithmetic progressions
• Utonality

 المراجع

• Sigler, Laurence E. (trans.) (2002). Fibonacci's Liber Abaci. Springer-Verlag. pp. 259–260. ISBN 0-387-95419-8.

 وصلات خارجية

• Hazewinkel, Michiel, ed. (2001), "Arithmetic series", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104 
• Eric W. Weisstein, Arithmetic progression at MathWorld.
• Eric W. Weisstein, Arithmetic series at MathWorld.