خوارزمية
الخوارزمية هي عبارة عن منهج فعال effective method يهدف لأداء مهمة أو حل مشكلة ما يعبر عنه بمجموعة محددة من التعليمات المتسلسلة لمعالجة حاسوبية، تهدف إلى الحصول على نتائج محددة اعتباراَ من معطيات ابتدائية». وسميت الخوارزمية بهذا الاسم نسبة إلى العالم المسلم الطاشقندي الأصل أبو جعفر محمد بن موسى الخوارزمي الذي كتب رسالة مهمة عن المنهج الجبري القرن التاسع الميلادي.[1] وأصله كما يدل اسمه من خوارزم، وقد عاش في بغداد من سنة 780م إلى 847م في عهد الخليفة المأمون. وقد برع هذا العالم في الرياضيات والفلك، وترك بصمات في التراث الحضاري العالمي، فقد وضع الخوارزمي مبادئ علم الجبر وألف كتاب «الجبر والمقابلة»، وهو أول من سمّى علم الجبر بهذا الاسم، ثم انتشر هذا العلم وانتقل اسمه إلى جميع اللغات تقريباَ. ألف الخوارزمي كتاباً في الحساب، ترجم إلى اللاتينية بعد ثلاثة قرون تحت عنوان Algoritmi de nemero indriun، ثم أطلق على جداول الضرب والقسمة والحساب العشري اسم Algorisms. ظلت هذه الكلمة متداولة في أوربا حتى أصبحت مصطلحاَ يحمل مدلولاً جديداً مرتبطاً بالبرمجة Algorithm. تستخدم ألفاظ أخرى للدلالة على بعض الخوارزميات المعينة كألفاظ الإجرائية procedure والمنهج method والتقنية technique. تسمى عملية تطبيق دخل على الخوارزمية لاستخراج خرج، بعملية التحسيب.
فعندما يُطلب من خبير في البرمجة أن يصنع برنامجاً، سواء لحل مسألة رياضية أو لاختراع لعبة أو لبناء برنامج تطبيقي يخدم أغراضاً محددة، فإن أول ما يفكر به المتخصص، بعد فهم المسألة ودراستها دراسة كافية، هو وضع استراتيجية للحل بطريقة تمكّن، فيما بعد، من ترجمة هذه الاستراتيجية إلى لغة يفهمها الحاسوب. تسمى هذه الاستراتيجية في أوساط المختصين بالبرمجة باسم «الخوارزمية».
تستخدم الخوارزميات في عمليات الحساب ومعالجة المعطيات والعديد من الحقول الأخرى. (في بعض الخيارات المتقدمة قد لا تكون التعليمات متسلسلة ولا حتى أن تكون منتهية، انظر خوارزمية غير حتمية nondeterministic algorithm).
كل خوارزمية هي عبارة عن قائمة بتعليمات معرفة ومحددة لأداء مهمة ما. تصف التعليمات عملية تحسيب يتم إجراؤها ليتم الانتقال من حالة ابتدائية إلى حالات متتابعة ومنتهية بحالة نهائية. وليس من الضروري أن يكون الانتقال من حالة إلى التي تليها حتمياً، فبعض الخوارزميات مثل الخوارزميات العشوائية randomized algorithms تتضمن نوعاً من العشوائية.
بدأ التشكل الجزئي للمفهوم مع محاولات حل "مشكلة القرار" Entscheidungsproblem التي طرحت من قبل ديفيد هيلبرت David Hilbert في عام 1928، ثم تطورت تشكلات لاحقة مع محاولات تعريف قابلية الحساب الفعال effective calculability[2]، أو المنهج الفعال [3]effective method، ومنها كانت التوابع العودية (التراجعية) لكل من Gödel (1930) وHerbrand (1934) وKleene (1935)، وتحليل لمبدا الذي طرحه Alonzo Church عام 1936، و"التشكيل 1" "Formulation 1" الذي طرحه Emil Post عام 1936، وآلة تورنگ التي طرحها آلان تورنگ في أواخر ثلاثينيات القرن العشرين.
عندما توصف خوارزمية ما بأنها "مستمرة" فإما أن يعني هذا أنها تنفذ على معطيات تمثل كميات مستمرة رغم أن هذه المعطيات تمثل بتقريب متقطع (تدرس مثل هذه الخوارميات في التحليل العددي) أو أنها خوارزمية في صيغة معادلة تفاضلية والتي تنفذ بشكل مستمر على المعطيات، وعلى حاسوب تماثلي[4].
أصل الكلمة
كلمة خوارزم (algorithm) في الأصل كانت مقتصرة على خوارزمية تتكون تراكيب الثلاثة فقط وهي: التسلسل (sequence) ، الاختيار (selection)، التكرار (repetition).
- التسلسل: تكون الخوارزمية عبارة عن مجموعة من التعليمات المتسلسلة، هذه التعليمات قد تكون إما بسيطة أو من النوعين التاليين.
- الاختيار: بعض المشاكل لايمكن حلها بتسلسل بسيط للتعليمات، وقد تحتاج إلى اختبار بعض الشروط وتنظر إلى نتيجة الاختبار، إذا كانت النتيجة صحيحة تتبع مسار يحوي تعليمات متسلسلة، وإذا كانت خاطئة تتبع مسار آخر مختلف من التعليمات. هذه الطريقة هي ماتسمى اتخاذ القرار أو الاختيار.
- التكرار: عند حل بعض المشاكل لا بد من إعادة نفس تسلسل الخطوات عدد من المرات. وهذا مايطلق عليه التكرار.
وقد أثُبت أنه لاحاجة إلى تراكيب إضافية.استخدام هذه التراكيب الثلاث يسهل فهم الخوارزمية واكتشاف الأخطاء الواردة فيها وتغييرها.
خصائص الخوارزمية
- مجموعة دقيقة من القواعد والتعليمات يفهمها الجميع
- تطبق على معطيات قابلة للتغيير
- تعطي نتيجة
- مجموعة منتهية من التعليمات
- تعرف مجال متحولات الدخل
- يجب أن تكون فعالة، أي زمن التنفيذ أقل من حد معين.
إن الصفات الأساسية التي تملكها الخوارزميات هي:
ـ أنها تتألف من مجموعة من القواعد الدقيقة التي يفهمها الجميع.
ـ تطبق على معطيات قابلة للتغيير.
ـ تسعى لبناء نتيجة نحصل عليها عندما يكون اختيار المعطيات ناجحاً.
إن التعريف الوارد في المقدمة غير كاف من وجهة نظر المعلوماتيين، إذ يعرِّف Knuth في كتابه «فن البرمجة» الخوارزمية، بأنها مجموعة من القواعد (أو التعليمات) التي تتميز بالصفات الآتية:
ـ يجب أن تكون هذه المجموعة منتهية، وتنتهي بعد عدد منته من العمليات.
ـ يجب أن تكون محددة ودقيقة، بمعنى أن كل تعليمة يجب أن توصف من دون لَبْس.
ـ يجب تحديد مجال تعريف المعطيات المُدخلة إن وجدت (أعداد صحيحة، حقيقية، أحرف،...).
ـ يجب أن يكون هنالك نتيجة (واحدة على الأقل).
ـ يجب أن تكون فعّالة، أي أن يتمكن شخص من تنفيذ العمليات كلها في وقت منته باستخدام الإمكانات اليدوية (دون حاسوب).
تعبِّر الخوارزمية وفق هذا التعريف عن طريقة منهجية لحل مسألة معينة، على وجه قابل للتنفيذ الآلي. وإذا كان وضع الخوارزمية يحتاج إلى مزيج من المنهجية والعلم والإبداع، فإن تنفيذها لا يترك مجالاً للتأويل والحدس.
وقد كان البحث عن الخوارزميات اللازمة لحل المسائل، وما زال، من القضايا الهامة في البحث والتطوير، فقد وضع الإنسان منذ القدم خوارزميات لرسم الأشكال الهندسية وحساب مساحاتها وحجومها، وجميع الطرائق التي تعلمناها لضرب الأعداد وقسمتها في المرحلة الابتدائية هي عبارة عن خوارزميات، وإن أقدم خوارزمية في التاريخ هي خوارزمية إقليدس حول حساب القاسم المشترك الأعظم لعددين صحيحين، التي وضعها في القرن الثالث قبل الميلاد، ومن أشهر الخوارزميات، تلك التي وضعها المصريون القدماء لرسم مثلث قائم الزوايا، والتي حوّلها فيثاغورث إلى نظرية شهيرة.
ومع التقدم التقني، وظهور الحواسيب، وقدرتها على تنفيذ التعليمات بسرعة فائقة، أصبح اهتمام المعلوماتيين منصباً على الخوارزميات لكونها مفتاح حل لمسائل كثيرة وبرمجتها. ولم تعد المواضيع التي تعالجها الخوارزميات تقتصر على الموضوعات الرياضية، بل تعدّتها إلى معالجة النصوص والرسوم والأصوات.
ولكن هل توجد خوارزمية واحدة لحل مسألة ؟ بالطبع لا؛ فمهما تكن المسألة بسيطة، قد توجد طرائق عدة لحلها. وإن اختيار الخوارزمية المناسبة لحل مسألة معينة، يتعلق بعدة عوامل: منها حجم المسألة والشكل الذي تطرح به، ونمط الأجهزة المستخدمة للحل وإمكاناتها.
وكمثال على ذلك، لنأخذ عملية حسابية بسيطة كضرب عددين موجبين، ولنفترض أن الإمكانات المتوفرة لدينا لإجرائها لا تزيد على الورقة والقلم. إن طريقة الضرب المعتمدة غالباً، ستكون بضرب أرقام العدد الأول بكل رقم من أرقام العدد الثاني على التوالي، ابتداءً من اليمين نحو اليسار، وترتب الإجابات بعضها تحت بعض، مع إجراء انزياح بمقدار مرتبة في كل مرة، وفي نهاية عمليات الضرب، تجرى عملية جمع أخيرة، وهذه هي الخوارزمية التقليدية للضرب.
من الممكن كذلك الحصول على النتيجة ذاتها بتطبيق الطريقة الروسية في الضرب، حيث يكتب العددان على سطر واحد، ثم يقسم العدد الأول على 2، ويوضع ناتج القسمة تحته مع إهمال باقي القسمة، إن لم يكن صفراً، ويضرب العدد الثاني بـ2 ويوضع الجداء تحته، تكرر العملية حتى يصبح الرقم في نهاية عمود العدد الأول مساوياً 1، ولإيضاح هذه الطريقة سنستخدمها في إجراء عملية الضرب 45 × 19.
| 19 | 45 |
| 38 | 22 |
| 76 | 11 |
| 152 | 5 |
| 304 | 2 |
| 608 | 1 |
في نهاية العملية تحذف الأسطر التي تحتوي عدداً زوجياً في عمود العدد الأول، ثم تجمع العناصر الموجودة في عمود العدد الثاني. ففي مثالنا نحذف السطر الذي يحتوي 22 و2 ثم نجمع:
19 + 76 + 152 + 608 = 855
قد يجد البعض هذه الطريقة في الضرب معقدة، ولكنها الطريقة المستخدمة في الدارات الإلكترونية للعديد من الحواسيب. وتتميز هذه الطريقة بأن تطبيقها لا يستدعي تخزين جداول الضرب، فكل ما يحتاج إليه المرء، هو معرفة إنجاز عمليات الجمع، والمضاعفة والقسمة على 2.
توجد خوارزميات أخرى لضرب الأعداد الصحيحة الكبيرة جداً، ولكنها أكثر تعقيداً، ومن ثم أكثر بطئاً عندما تكون الأعداد صغيرة.
التمثيل
خوارط الانسياب
خوارط الانسياب هي تمثيل مصور للخوارزمية يوضح خطوات حل المشكلة من البداية إلى النهاية مع إخفاء التفاصيل لإعطاء الصورة العامة للحل. ويمكن تصنيفها إلى أصناف أربعة هي:
- مخططات سير العمليات التتابعية (Sequential Flowcharts).
- مخططات سير العمليات ذات التفرع (Branched Flowcharts).
- مخططات سير العمليات ذات التكرار والدوران (Loop Flowcharts).
- محططات سير العمليات ذات الاختيار (Selection Flowcharts) .
2الشفرة المزيفة
تمثيل الخوارزمية بلغات البشر كالانجليزية أو الفرنسية أو العربية أو بلغات البرمجة كالباسكال (Pascal).البعض يستخدم الكثير من التفاصيل و البعض الآخر يستخدم القليل ... فلا قاعدة معينة لكتابة هذا النوع من الشفرات.
قواعد البرمجة الأربع:
- التكرار Looping
- التفرع Branching
- الاختيار Selection
- التتابع Sequence
التعليمات
- القراءة
إقرأ <اسم المتحول>
مثال : إقرأ x
- الكتابة
اكتب <صيغة exprision>
مثال : اكتب x*4
اكتب " لا يوجد حل للمعادلة"
- الاسناد
<صيغة> ——> <متحول>
مثال : x <—— x*4
- التعليمة الشرطية
اذا <شرط> نفذ
[<مجموعة من التعليمات 1>]
وإلا
[<مجموعة من التعليمات 2>]
- التكرار
مادام <شرط> كرّر
[<مجموعة من التعليمات>]
طرائق التعبير عن الخوارزمية
يواجهنا هنا سؤال هام، وهو: كيف يكون التعبير عن الخوارزمية؟ هل يكون باللغة المتداولة كالعربية أو الإنكليزية، والكتابة بلغة إنشائية شرحاً عن خطوات الحل؟ من الواضح أن هذا الحل تواجهه عقبات كثيرة، فإذا كان الشرح لعملية الضرب وفق الطريقة الروسية باللغة المتداولة، فإن ذلك، ليس بدهياً، وقد لا يكون واضحاً. أما التعبير عن الطريقة التقليدية في الضرب باللغة الطبيعية فهو عملية أصعب.
وهنا اقترحتُ عدة طرائق بعضها نصّية (عبارات) والأخرى بيانية (مخططات).
الطرائق النصية
إن أفضل طريقة لتجنب الالتباس المحتمل وروده عند التعبير باللغة المتداولة، هي استخدام إحدى لغات البرمجة التي تتميز بصيغ قواعدية تحدّ من إمكانات الالتباس هذه، وهذا يعني التعبير عن الخوارزمية بالبرنامج. ولكن الكتابة بلغة برمجة ما يعني التقيد بلغة خاصة، في حين أن المطلوب وسيلة تعبير مستقلة عن أية لغة. إن استخدام طريقة منتظمة للتعبير عن الخوارزمية يوفر حرية التعبير عن الحل مع الاحتفاظ بسهولة نقل الحل إلى لغة برمجة يفهمها الحاسوب، يمكن أن تسمى هذه الطريقة في التعبير عن الخوارزمية تجاوزاً لغة خوارزمية pseudo-code وترجمتها الحرفية «شبه الترميز» إذ تشكل حلاً وسطاً بين لغتنا الطبيعية ولغات البرمجة.
أ ـ اللغة الخوارزمية
تُعرّف في هذه اللغة الخوارزمية العناصر الآتية:
المتحول: وهو الغرض الذي تجري معالجته ضمن الخوارزمية، وتكون قيمته متحولة (قابلة للتغيير)، ويعرف باسم خاص متميز.
الثابت: وهو غرض قيمته غير متغيرة طوال البرنامج، ويعر ف باسم خاص.
الصيغة: وتتألف من متحولات وثوابت وعمليات حسابية أو منطقية.
يمكن التعبير عن مسار الحل لمسألة أو توصيف خوارزمية بوساطة التعليمات أو الأوامر الأساسية الخمسة الآتية:
1ـ تعليمة القراءة: وهي قراءة قيمة من الدخل (من لوحة المفاتيح) لوضعها في خانة ذاكرة، وشكل التعليمة:
اقرأ < اسم المتحول >
2ـ تعليمة الكتابة: وهي كتابة قيمة معينة على وحدة الخرج (الشاشة)، وشكل التعليمة:
اكتب < صيغة >
3ـ تعليمة الإسناد: وهي إسناد قيمة محددة أو نتيجة صيغة لمتحول (خانة ذاكرة)، وشكل التعليمة:
< صيغة > ¬ < اسم المتحول >
4ـ التعليمة الشرطية: وترد بأحد الشكلين الآتيين:
أ ـ التنفيذ بشرط: ونعبر عن ذلك كما يأتي:
إذا < شرط > نفّذ
< مجموعة تعليمات 1>
ب ـ التعليمة الشرطية الاختيارية: وتسمح بالاختيار بين طريقتي تنفيذ وذلك وفق شرط.
إذا < شرط > نفّذ
< مجموعة تعليمات 1>
وإلا
< مجموعة تعليمات 1>
5 ـ التعليمة التكرارية: وتستعمل لتكرار مجموعة من التعليمات مادام شرط محدد محققا، أي يتكرر تنفيذ مجموعة من العمليات ما دامت الصيغة المنطقية للشرط صحيحة.
مادام < شرط > كرر
< مجموعة تعليمات >
ـ كيفية الوصول إلى الخوارزمية؟
للوصول إلى وضع الخوارزمية المناسبة لحل مسألة معينة، تُتَّبع الخطوات الآتية:
1- فهم المسألة وتحليلها بدقة، أي معرفة المدخلات (المعطيات) المطلوب معالجتها والمخرجات (النتائج) المطلوب الحصول عليها، وصياغة هذه المعلومات بوضوح ما أمكن، ويمكن استخدام العلاقات الرياضية التي توصف علاقة الدخل بالخرج (إن وجدت مثل هذه العلاقات).
2- تصور شامل لحل المسألة، ومن ثم تجزئة هذا الحل إلى خطوط عريضة تمثل الوظائف الأساسية، ثم يعاد النظر في كل وظيفة أساسية معقدة، وكأنها مسألة جديدة تتطلب حلاً، وتتألف بدورها من عدة خطوات جزئية، وهكذا....، ويُحرص دوماً على استخدام هياكل التعليمات الأساسية حين الحاجة (التكرار والتفرع الشرطي). تكرر هذه الآلية إلى حين الوصول إلى عمليات يمكن التعبير عنها مباشرة بالتعليمات البسيطة (قراءة، كتابة، إسناد، حساب)، وتسمى هذه العملية التبسيط المتتالي أو الطريقة النزولية.
3- عند الوصول إلى أدنى المستويات تنتج خوارزمية كاملة مكتوبة باللغة الخوارزمية، واعتماداً على هذه الخوارزمية يجري الترميز باللغة المناسبة (....,Java, C++, C, Pascal).
الطرائق البيانية
تعتمد الطريقة البيانية لصياغة الخوارزميات على توضيح خطوات تنفيذ الخوارزمية باستخدام أشكال هندسية خاصة وأسهم تصل بينها، إضافة إلى عبارات باللغة الطبيعية، وتعابير رياضية أو منطقية، وبذلك ينتج ما يسمى بالمخطط التدفقي (flowchart diagram). ونلاحظ هنا أن الأسهم تفصّل العمليات اللازمة لإنجاز العمل، وتبيّن تسلسلها.
يستخدم المخطط التدفقي أشكالا ًهندسية متفقاً عليها، خصّص كل منها لنوع من العمليات. فقد استخدمت الشكل البيضوي لتحديد بداية الخوارزمية ونهايتها، كما استخدم المستطيل للعمليات التنفيذية العادية، أما العمليات التي ترتبط باختيار تحقق شرط وتتطلب قراراً منطقياً، فقد استخدم لها شكل المعيّن.
مثال:
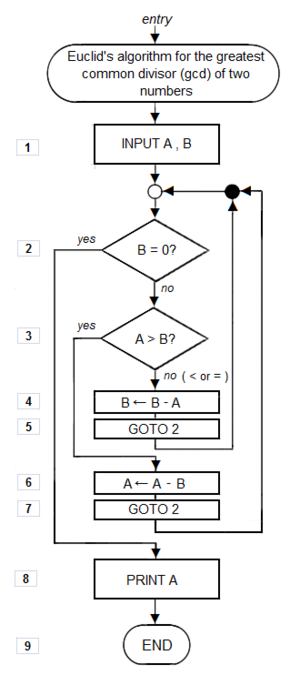
تستخدم في هذا المثال هذه الرموز للتعبير عن خوارزمية لقسمة عدد صحيح على عدد صحيح آخر. ليكن العدد المقسوم n والعدد القاسم d والناتج m والباقي r. هنا يجري طرح d من r طالما أن r أكبر من d وتكرر العملية حتى يغدو r أصغر من d فيكتب الناتج m والباقي r.
تعقيد الخوارزميات
تبين أنه لحل مسألة بالحاسوب، لابد من إيجاد خوارزمية لها، ولكن إيجاد الخوارزمية غير كاف دوماً، إذ قد يبلغ زمن تنفيذها بالحاسوب زمناً يتجاوز مدة حياة المبرمج نفسه، فمثلاً، لعبة الشطرنج مسألة تنتهي بعد عدد محدود من الحركات، ولكن يوجد عملياً 1910 حركة يجب مناقشتها، وهذا يتطلب ملايين السنين لتنفيذها.
وهكذا يكون معرفة متطلبات الخوارزمية من حيث الزمن اللازم للتنفيذ وحجوم التخزين أمراً هاماً جداً، وهو الهدف الأساسي من تحليل الخوارزميات، وبذلك ينتج معيار لمقارنة خوارزميتين لحل مسألة واحدة، وللمفاضلة بينهما، كما يصبح لدى الباحثين حافز للبحث عن خوارزميات أخرى لحل المسائل ذاتها ولكن بمتطلبات أفضل.
1- دراسة تعقيد الخوارزميات
في دراسة تعقيد الخوارزميات يكون الاهتمام بنوعين من التعقيد:
1ـ التعقيد الحجمي أو المكاني space complexity: ونقصد به تقدير حجم الذواكر اللازم للخوارزمية.
2ـ التعقيد الزمني time complexity: ونقصد بذلك التقدير الزمني. وهنا، يجب البدء أولاً باختيار واحدة لقياس هذا التعقيد، وقد اقترح بعضهم اعتبار مدة تنفيذ البرنامج واحدة للقياس، لكن هذه الواحدة لا تصلح بسبب اختلاف الحواسيب وسرعة معالجاتها. كما اقترح البعض الآخر اعتبار عدد التعليمات واحدة للقياس، لكن هذه الواحدة لا تصلح أيضاً بسبب اختلاف عدد التعليمات التي نكتب بها البرنامج باختلاف لغة البرمجة المستخدمة وأسلوب المبرمج. وربما كان أفضل ما اقترح في هذا المضمار هو عدد العمليات الأساسية المستخدمة في الخوارزمية، لأنه يعطي فكرة جيدة عن أداء الخوارزمية، على وجه مستقل عن تفاصيـل التنفيذ، ولكن ما المقصود بالعمليات الأساسية؟
تختلف العمليات الأساسية باختلاف طبيعة الخوارزمية بحسب ما يبينه الجدول التالي:
| الخوارزمية | العمليات الأساسية |
|---|---|
| البحث عن اسم شخص ما X في قائمة أسماء |
البحث عن اسم شخص ما X في قائمة أسماء |
| ضرب مصفوفتين | ضرب عددين |
| فرز مصفوفتين | مقارنة عنصرين |
وبديهي أن عدد العمليات الأساسية يختلف باختلاف حجم معطيات الدخل.
يفترض في الحالة العامة أن حجم معطيات الدخل (وهو عدد عناصر هذه القائمة) هو n، فيكون هناك في أسوأ الحالات n عملية مقارنة، وبذلك يمكن تعريف التعقيد الزمني لخوارزمية بأنه مرتبة كبر أسوأ الحالات.
يستخدم عادة تدوين لاندو للدلالة على التعقيد، فإذا كان التعقيد من رتبة n3 يُقال أن التعقيد هو O (n3).
2- أهمية تعقيد الخوارزميات عملياً
إن تحليل تعقيد الخوارزميات أمر على جانب كبير من الأهمية، إذ يسمح بانتقاء أفضل الخوارزميات المقترحة، أو البحث عن خوارزمية أفضل للحل.
يبين الجدول 2 كيف تنعكس رتبة تعقيد خوارزمية على زمن التنفيذ، من أجل قيم مختلفة لحجم معطيات الدخل.
3- مثال تحليل خوارزمية:
يقدر تعقيد البرامج تقديراً عملياً بحساب العدد الأعظمي للدوران في الحلقات التعليمات التكرارية بدلالة حجم معطيات الدخل.
يمكن على سبيل المثال تطبيق هذا التقدير على خوارزمية ضرب المصفوفات.
لتكن لدينا مصفوفتان من الأعداد الحقيقية B,A و ، (A= (aij) B = (bij)) بُعد كل منهما هو n * n.
وليكن المطلوب حساب المصفوفة C = A * B.
يعطى ضرب مصفوفتين بالصيغة الرياضية الآتية:
| تعقيد الخوارزمية | ||||||
| حجم معطيات الدخل | n | n log2n | n² | n² | n³ | nn |
| 10 | 10 | 33 | 100 | 1000 | 1024 | 1010 |
| 100 | 100 | 660 | 104 | 106 | 1010 | 10200 |
| 1000 | 1000 | 104 | 106 | 109 | 10330 | 103000 |
إن العملية الأساسية هنا هي الضرب، وهناك لكل عنصر من المصفوفة C، n عملية ضرب داخل حلقة k.
ولما كان هناك n2 عنصراً في C فإن عدد عمليات الضرب هو n3.
ومن ثَمَّ فإن درجة تعقيد الخوارزمية هو O (n3).
إن إيجاد الخوارزمية الفُضْلى من حيث التعقيد الزمني والحجمي ليس بالأمر السهل، فغالباً ما يكون اختيار البنية التي تحقق وفراً أكبر في حجوم التخزين مدعاة إلى عمليات أكثر، ومن ثَمَّ إلى تعقيد زمني أكبر، وبالعكس فإن الخوارزمية ذات التعقيد الزمني الأقل تكون غالباً مرتبطة ببنية أقل توفيراً في حجوم التخزين، ومن هنا لا يزال الباب مفتوحاً أمام الباحثين للبحث عن خوارزميات ذات توفير مزدوج في الحجم والذاكرة.
أنواع الخوارزميات
يمكن تصنيف الخوارزميات بحسب الوظيفة التي تقوم بها، والمسألة الرئيسية التي تحلها، ومن ثم يمكن أن نتكلم مثلاً عن:
ـ خوارزميات البحث search algorithm (هدفها البحث عن عنصر معطيات محدد في بنية معطيات)،
ـ خوارزميات الفرز sort algorithm (هدفها ترتيب مجموعة من عناصر المعطيات ترتيباً متتالياً اعتماداً على أحد بنود العناصر أو على اجتماع عدة بنود محددة).
كما يمكن اتباع أسلوب آخر في التصنيف يعتمد على التقنية المستخدمة في تشكيل التعليمات وتسلسلها، فنتكلم مثلاً عن:
ـ الخوارزميات التتابعية sequential algorithm (يجري تنفيذها لاحقاً وفق تتابع التعليمات وبترتيب معين)،
ـ الخوارزميات المتوازية parallel algorithm (يجري تنفيذ أكثر من جزء منها في آن واحد معاً، ويجري ذلك عادة على عدة معالجات)،
ـ الخوارزميات الرجوعية backtracking algorithm (وهي خوارزميات تستخدم لإيجاد حل ضمن مجموعة محاولات ممكنة، حيث تمثل المحاولات على شكل فروع في شجرة. يجري تجريب أحد الفروع، فإن لم نجد الحل نعود إلى الوراء لنختار مساراً آخر نجربه وهكذا، حتى نعثر على المسار المناسب)،
ـ الخوارزميات العَوْدية recursive algorithm (وهي خوارزميات تستخدم ضمن تعليماتها استدعاءً للخوارزمية نفسها)، وغير ذلك.[5]
خوارزميات الحاسوب

الأمثلة
 مقالة مفصلة: أمثلة خوارزمية
مقالة مفصلة: أمثلة خوارزمية
أمثلة خوارزمية
خوارزمية إقليدس

أمثلة
أمثلة من 1599 و650:
| خطوة 1 | 1599 = 650*2 + 299 |
| خطوة 2 | 650 = 299*2 + 52 |
| خطوة 3 | 299 = 52*5 + 39 |
| خطوة 4 | 52 = 39*1 + 13 |
| خطوة 5 | 39 = 13*3 + 0 |
لغة الحاسوب لخوارزمية إقليدس
برنامج غير كامل لخوارزمية إقليدس
اختبار خوارزميات اقليدس
قياس وتحسين خوارزميات اقليدس
تحليل حسابي
 مقالة مفصلة: تحليل الخوارزميات
مقالة مفصلة: تحليل الخوارزميات
الاصطلاحية مقابل التجريبية
 مقالات مفصلة: الخوارزميات التجريبية
مقالات مفصلة: الخوارزميات التجريبية- التنميط (برمجة الكمبيوتر)
- برنامج التحسين
FFT speedup
 مقالة مفصلة: تأثير خوارزمي
مقالة مفصلة: تأثير خوارزمي
التصنيف
خوارزميات مستمرة
المسائل القانونية
التاريخ: تطوير مفهوم "الخوارزمية"
انظر أيضاً
- آلة مجردة
- خصائص خوارزمية
- تصميم خوارزميات
- كفاءة خوارزمية
- هندسة خورازميات
- أمثلة خوارزمية
- موسيقى خوارزمية
- Algorithmic synthesis
- تجارة خوارزمية
- بنى معطيات
- Garbage In, Garbage Out
- Heuristics
- Important algorithm-related publications
- مقدمة الخوارزمية
- قائمة موضوعات الخوارزمية
- قائمة الخوارزميات
- Numerical Mathematics Consortium
- وظيفة جزئية
- Profiling (computer programming)
- Program optimization
- خوارزمية عشوائية وخوارزمية كمومية
- نظرية التحسيب
- الحسوبية (جزء من نظرية الحسوبية)
- نظرية التعقيد التحسيبي
الهوامش
- ^ إيريك وينستاين، "Algorithm" من موقع MathWorld.
- ^ Kleene 1943 in Davis 1965:274
- ^ Rosser 1939 in Davis 1965:225
- ^ Adaptation and learning in automatic systems, page 54, Ya. Z. Tsypkin, Z. J. Nikolic, Academic Press, 1971, ISBN 978-0-12-702050-1
- ^ غيداء ربداوي. "الخوارزمية". الموسوعة العربية.
المصادر
- Axt, P. (1959) On a Subrecursive Hierarchy and Primitive Recursive Degrees, Transactions of the American Mathematical Society 92, pp. 85–105
- Bell, C. Gordon and Newell, Allen (1971), Computer Structures: Readings and Examples, McGraw-Hill Book Company, New York. ISBN 0-07-004357-4}.
- Blass, Andreas; Gurevich, Yuri (2003). "Algorithms: A Quest for Absolute Definitions" (PDF). Bulletin of European Association for Theoretical Computer Science. 81. Includes an excellent bibliography of 56 references.
- Boolos, George; Jeffrey, Richard (1974, 1980, 1989, 1999). Computability and Logic (4th ed.). Cambridge University Press, London. ISBN 0-521-20402-X.
{{cite book}}: Check date values in:|year=and|date=(help); Invalid|ref=harv(help); More than one of|author=and|last1=specified (help)CS1 maint: date and year (link): cf. Chapter 3 Turing machines where they discuss "certain enumerable sets not effectively (mechanically) enumerable". - Burgin, M. Super-recursive algorithms, Monographs in computer science, Springer, 2005. ISBN 0-387-95569-0
- Campagnolo, M.L., Moore, C., and Costa, J.F. (2000) An analog characterization of the subrecursive functions. In Proc. of the 4th Conference on Real Numbers and Computers, Odense University, pp. 91–109
- Church, Alonzo (1936a). "An Unsolvable Problem of Elementary Number Theory". The American Journal of Mathematics. 58 (2): 345–363. doi:10.2307/2371045. Reprinted in The Undecidable, p. 89ff. The first expression of "Church's Thesis". See in particular page 100 (The Undecidable) where he defines the notion of "effective calculability" in terms of "an algorithm", and he uses the word "terminates", etc.
- Church, Alonzo (1936b). "A Note on the Entscheidungsproblem". The Journal of Symbolic Logic. 1 (1): 40–41. doi:10.2307/2269326.
{{cite journal}}: More than one of|number=and|issue=specified (help) Church, Alonzo (1936). "Correction to a Note on the Entscheidungsproblem". The Journal of Symbolic Logic. 1 (3): 101–102. doi:10.2307/2269030.{{cite journal}}: More than one of|number=and|issue=specified (help) Reprinted in The Undecidable, p. 110ff. Church shows that the Entscheidungsproblem is unsolvable in about 3 pages of text and 3 pages of footnotes. - Daffa', Ali Abdullah al- (1977). The Muslim contribution to mathematics. London: Croom Helm. ISBN 0-85664-464-1.
- Davis, Martin (1965). The Undecidable: Basic Papers On Undecidable Propositions, Unsolvable Problems and Computable Functions. New York: Raven Press. ISBN 0486432289. Davis gives commentary before each article. Papers of Gödel, Alonzo Church, Turing, Rosser, Kleene, and Emil Post are included; those cited in the article are listed here by author's name.
- Davis, Martin (2000). Engines of Logic: Mathematicians and the Origin of the Computer. New York: W. W. Nortion. ISBN 0393322297. Davis offers concise biographies of Leibniz, Boole, Frege, Cantor, Hilbert, Gödel and Turing with von Neumann as the show-stealing villain. Very brief bios of Joseph-Marie Jacquard, Babbage, Ada Lovelace, Claude Shannon, Howard Aiken, etc.
- قالب:DADS
- Dennett, Daniel (1995). Darwin's Dangerous Idea. New York: Touchstone/Simon & Schuster. ISBN 0684802902.
- Yuri Gurevich, Sequential Abstract State Machines Capture Sequential Algorithms, ACM Transactions on Computational Logic, Vol 1, no 1 (July 2000), pages 77–111. Includes bibliography of 33 sources.
- Kleene C., Stephen (1936). "General Recursive Functions of Natural Numbers". Mathematische Annalen. 112 (5): 727–742. doi:10.1007/BF01565439. Presented to the American Mathematical Society, September 1935. Reprinted in The Undecidable, p. 237ff. Kleene's definition of "general recursion" (known now as mu-recursion) was used by Church in his 1935 paper An Unsolvable Problem of Elementary Number Theory that proved the "decision problem" to be "undecidable" (i.e., a negative result).
- Kleene C., Stephen (1943). "Recursive Predicates and Quantifiers". American Mathematical Society Transactions. 54 (1): 41–73. doi:10.2307/1990131.
{{cite journal}}: More than one of|number=and|issue=specified (help) Reprinted in The Undecidable, p. 255ff. Kleene refined his definition of "general recursion" and proceeded in his chapter "12. Algorithmic theories" to posit "Thesis I" (p. 274); he would later repeat this thesis (in Kleene 1952:300) and name it "Church's Thesis"(Kleene 1952:317) (i.e., the Church thesis). - Kleene, Stephen C. (First Edition 1952). Introduction to Metamathematics (Tenth Edition 1991 ed.). North-Holland Publishing Company. ISBN 0720421039.
{{cite book}}: Check date values in:|year=(help) Excellent—accessible, readable—reference source for mathematical "foundations". - Knuth, Donald (1997). Fundamental Algorithms, Third Edition. Reading, Massachusetts: Addison–Wesley. ISBN 0201896834.
- Kosovsky, N. K. Elements of Mathematical Logic and its Application to the theory of Subrecursive Algorithms, LSU Publ., Leningrad, 1981
- Kowalski, Robert (1979). "Algorithm=Logic+Control". Communications of the ACM. 22 (7): 424–436. doi:10.1145/359131.359136. ISSN 0001-0782.
- A. A. Markov (1954) Theory of algorithms. [Translated by Jacques J. Schorr-Kon and PST staff] Imprint Moscow, Academy of Sciences of the USSR, 1954 [i.e., Jerusalem, Israel Program for Scientific Translations, 1961; available from the Office of Technical Services, U.S. Dept. of Commerce, Washington] Description 444 p. 28 cm. Added t.p. in Russian Translation of Works of the Mathematical Institute, Academy of Sciences of the USSR, v. 42. Original title: Teoriya algerifmov. [QA248.M2943 Dartmouth College library. U.S. Dept. of Commerce, Office of Technical Services, number OTS 60-51085.]
- Minsky, Marvin (1967). Computation: Finite and Infinite Machines (First ed.). Prentice-Hall, Englewood Cliffs, NJ. ISBN 0131654497. Minsky expands his "...idea of an algorithm—an effective procedure..." in chapter 5.1 Computability, Effective Procedures and Algorithms. Infinite machines."
- Post, Emil (1936). "Finite Combinatory Processes, Formulation I". The Journal of Symbolic Logic. 1 (3): 103–105. doi:10.2307/2269031. Reprinted in The Undecidable, p. 289ff. Post defines a simple algorithmic-like process of a man writing marks or erasing marks and going from box to box and eventually halting, as he follows a list of simple instructions. This is cited by Kleene as one source of his "Thesis I", the so-called Church–Turing thesis.
- Rosser, J.B. (1939). "An Informal Exposition of Proofs of Godel's Theorem and Church's Theorem". Journal of Symbolic Logic. 4. Reprinted in The Undecidable, p. 223ff. Herein is Rosser's famous definition of "effective method": "...a method each step of which is precisely predetermined and which is certain to produce the answer in a finite number of steps... a machine which will then solve any problem of the set with no human intervention beyond inserting the question and (later) reading the answer" (p. 225–226, The Undecidable)
- Sipser, Michael (2006). Introduction to the Theory of Computation. PWS Publishing Company. ISBN 053494728X.
- Stone, Harold S. (1972). Introduction to Computer Organization and Data Structures (1972 ed.). McGraw-Hill, New York. ISBN 0070617260. Cf. in particular the first chapter titled: Algorithms, Turing Machines, and Programs. His succinct informal definition: "...any sequence of instructions that can be obeyed by a robot, is called an algorithm" (p. 4).
- Turing, Alan M. (1936–7). "On Computable Numbers, With An Application to the Entscheidungsproblem". Proceedings of the London Mathematical Society, Series 2. 42: 230–265. doi:10.1112/plms/s2-42.1.230.
{{cite journal}}: Check date values in:|year=(help). Corrections, ibid, vol. 43(1937) pp. 544–546. Reprinted in The Undecidable, p. 116ff. Turing's famous paper completed as a Master's dissertation while at King's College Cambridge UK. - Turing, Alan M. (1939). "Systems of Logic Based on Ordinals". Proceedings of the London Mathematical Society, Series 2. 45: 161–228. doi:10.1112/plms/s2-45.1.161. Reprinted in The Undecidable, p. 155ff. Turing's paper that defined "the oracle" was his PhD thesis while at Princeton USA.
- United States Patent and Trademark Office (2006), 2106.02 **>Mathematical Algorithms< - 2100 Patentability, Manual of Patent Examining Procedure (MPEP). Latest revision August 2006
مراجع ثانوية
- Bolter, David J. (1984). Turing's Man: Western Culture in the Computer Age (1984 ed.). The University of North Carolina Press, Chapel Hill NC. ISBN 0807815640., ISBN 0-8078-4108-0 pbk.
- Dilson, Jesse (2007). The Abacus ((1968,1994) ed.). St. Martin's Press, NY. ISBN 031210409X., ISBN 0-312-10409-X (pbk.)
- van Heijenoort, Jean (2001). From Frege to Gödel, A Source Book in Mathematical Logic, 1879–1931 ((1967) ed.). Harvard University Press, Cambridge, MA. ISBN 0674324498., 3rd edition 1976[?], ISBN 0-674-32449-8 (pbk.)
- Hodges, Andrew (1983). Alan Turing: The Enigma ((1983) ed.). Simon and Schuster, New York. ISBN 0671492071., ISBN 0-671-49207-1. Cf. Chapter "The Spirit of Truth" for a history leading to, and a discussion of, his proof.
قراءات أخرى
- David Harel, Yishai A. Feldman, Algorithmics: the spirit of computing, Edition 3, Pearson Education, 2004, ISBN 0-321-11784-0
- Jean-Luc Chabert, Évelyne Barbin, A history of algorithms: from the pebble to the microchip, Springer, 1999, ISBN 3-540-63369-3
- Jean-Luc Chabert, Évelyne Barbin, A history of algorithms: from the pebble to the microchip, Springer, 1999, ISBN 3-540-63369-3
- David Harel, Yishai A. Feldman, Algorithmics: the spirit of computing, Edition 3, Pearson Education, 2004, ISBN 0-321-11784-0
- Knuth, Donald E. (2000). Selected Papers on Analysis of Algorithms. Stanford, California: Center for the Study of Language and Information.
- Knuth, Donald E. (2010). Selected Papers on Design of Algorithms. Stanford, California: Center for the Study of Language and Information.
- David Berlinski, The Advent of the Algorithm: The 300-Year Journey from an Idea to the Computer, Mariner Books, 2001, ISBN 978-0-15-601391-8
وصلات خارجية
- Algorithms at the Open Directory Project
- Eric W. Weisstein, Algorithm at MathWorld.
- Dictionary of Algorithms and Data Structures—National Institute of Standards and Technology
- Algorithms and Data Structures by Dr Nikolai Bezroukov
- Algorithm repositories
- The Stony Brook Algorithm Repository—State University of New York at Stony Brook
- Netlib Repository—University of Tennessee and Oak Ridge National Laboratory
- Collected Algorithms of the ACM—Association for Computing Machinery
- The Stanford GraphBase—Stanford University
- Combinatorica—University of Iowa and State University of New York at Stony Brook
- Library of Efficient Datastructures and Algorithms (LEDA)—previously from Max-Planck-Institut für Informatik
- Lecture notes
- Algorithms Course Materials. Jeff Erickson. University of Illinois.




