نقطة ناگل

نقطة ناگل باللون الأزرق

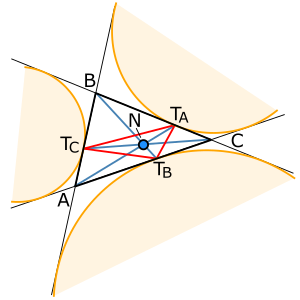
في الهندسة الرياضية، نقطة ناگل هي نقطة موجودة في أي مثلث، حيث في مثلث ABC بطول أضلاع a = |BC|، b = |CA|، c = |AB|، ليكن T_A، T_B، T_A هي النقاط التي تتقاطع فيها الدائرة الخارجية A مع المستقيم BC، الدائرة الخارجية B مع المستقيم CA والدائرة الخارجية C مع المستقيم AB على الترتيب. تتقاطع المستقيمات AT_A, BT_B, CT_C في نقطة N هي نقطة ناگل.

نقطة ناگل مسماة على اسم عالم الرياضيات الألماني من القرن التاسع عشر كرستيان هاينريش فون ناگل.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 العلاقة بمراكز المثلث الأخرى

نقطة ناگل هي isotomic conjugate لنقطة جرگون. نقطة ناگل، the incenter, and the centroid are collinear. The incenter is the Nagel point of the medial triangle (Anonymous 1896); equivalently, the Nagel point is the incenter of the anticomplementary triangle.

 الإحداثيات ثلاثية الخطوط

الإحداثيات ثلاثية الخطوط لنقطة ناگل حددهم گالاتلي (1913) كالتالي

$\csc ^{2}(A/2)\,:\,\csc ^{2}(B/2)\,:\,\csc ^{2}(C/2)$

ويعادل ذلك:

${\frac {b+c-a}{a}}\,:\,{\frac {c+a-b}{b}}\,:\,{\frac {a+b-c}{c}}.$

 انظر أيضاً

• Splitter (geometry)
• مركز المثلث

 مراجع

• Anonymous (1896). "Problem 73". American Mathematical Monthly. 3 (12): 329.

• Baptist, Peter (1987). "Historische Anmerkungen zu Gergonne- und Nagel-Punkt". Sudhoffs Archiv für Geschichte der Medizin und der Naturwissenschaften. 71 (2): 230–233. قالب:MathSciNet.

• Gallatly, William (1913). The Modern Geometry of the Triangle (2nd ed. ed.). London: Hodgson. pp. page 20. {{cite book}}: |edition= has extra text (help); |pages= has extra text (help)

 وصلات خارجية

• Eric W. Weisstein, Nagel Point at MathWorld.