نظرية طالس

اذا كان AC قطراً في الدائرة يكون المثلث ABC قائم في B.

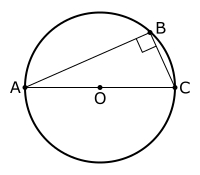
في الهندسة الرياضية تقول مبرهنة تالس أنّه إذا كانت A و B و C نقاط على دائرة حيث AC قطر لهذه الدّائرة تكون الزّاوية ABC زاوية قائمة.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 بيان النظرية

رسم للبيان.

نستعمل الحقائق التّالية

• مجموع الزوايا في مثلث مساو لمجموع زاويتين قائمتين 180°
• زاويتي قاعدة مثلّث متقايس الضّلعين متساويتان.
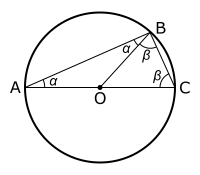
• لتكن O مركز الدّائرة. بما أنّ OA = OB = OC يكون OAB و OBC مثلثان متقايسا الضّلعين و بما أنّ زاويتي القاعدة في مثلث متقايس الضّلعين متساويتان ينتج أن OBC = OCB ، ABO = BAO لتكن BAO = β و OBC = α

تكون الزوايا الدّاخلية في المثلث ABC هي α ، β ، α + β

• بما أن مجموع زاويتي في مثلث هي مساوية لمجموع زاويتين قائمتين يكون

• $\alpha +\left(\alpha +\beta \right)+\beta =180^{\circ }$

إذاً

$2\alpha +2\beta =180^{\circ }$

إذاً

$\alpha +\beta =90^{\circ }$

في بعض الدّول الأوروبية مثل فرنسا ترمز نظرية طالس لنظرية مغايرة لما تقدم راجعها هنا، مبرهنة تالس.

 النظرية المعاكسة

تقول النظرية المعاكسة لطالس أن وتر مثلث قائم هو قطر الدائرة المحيطة به. عند الدمج بين النظريتين نحصّل على

• مركز الدّائرة المحيطة لمثلث يوجد على واحد من أضلع المثلّث يعني المثلث قائم.

 روابط خارجيّة

- *Munching on Inscribed Angles *Thales' theorem explained With interactive animation

• Eric W. Weisstein, مبرهنة تالس at MathWorld.