منصف زاوية صلبة

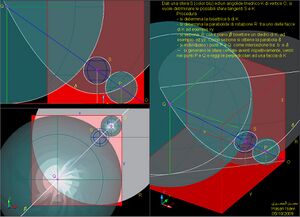
منصف زاوية صلبة هو الخط c الذي يمر برأس الزاوية وبمركز كرة متماسة للمستويات الثلاثة المكونة الزاوية نفسها.

يحدد المنصف c كتقاطع بين المستويات المنصفة للزاوايا الزوجية المكونة الزاوية الصلبة.

كرات متماسة المستويات المكونة لزاوية ثلاثية صلبة .يمثل الخط الذي يمر برأس الزاوية الصلبة المحل الهندسي للنقاط التي لها نفس البعد بالنسبة لمستويات الزاوية الصلبة

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 منصف زاوية زوجية

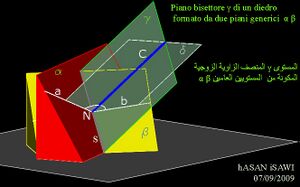
منصف زاوية زوجية Θ هو المستوى γ الذي يمثل المحل الهندسي لكل النقاط التي لها نفس البعد عن المستوين α β المكونين Θ. وبهذا كلُ نقطة تنتمي إلى γ هي مركز لكرة متماسة المستويين α β. لايجاد منصف الزاوية γ بين مستوين α β، من الضروري تحديد خطين c و s بحيث ينتميان إلى γ، حيث c هو أي خط منصف زاوية المقطع القائم للمستوين α β, اما s فهو الخط المشترك لنفس المستويين α β.

المقطع القائم (sezione retta) لزاوية الزوجية Θ، يتم الحصول عليه عن طريق قطع المستويين α β بمستوى ثالث عمودي على خط تقاطعهما.

المستوى γ ينصف الزاوية الزوجية المكونة من المستويين α β