مستقيم أويلر
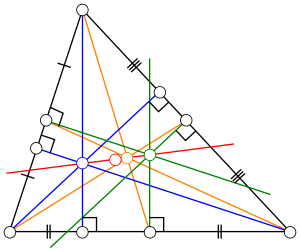
في الهندسة الرياضية، سمي مستقيم أويلر على اسم ليونهارد أويلر وهو مستقيم محدد في أي مثلث غير متساوي الأضلاع حيث يمر من عدة نقاط هامة محددة في المثلث. في الشكل يظهر مستقيم أويلر باللون الأحمر حيث يمر من نقطة تقاطع ارتفاعات المثلث (لون أزرق)، مركز الدائرة المحيطة (لون أخضر)، نقطة مركزية المثلث (لون برتقالي) ومركز دائرة النقاط التسعة (لون أحمر). حيث برهن أويلر في عام 1767 أن هذه النقاط الأربعة تقع على استقامة واحدة. وتتطابق هذه النقاط الأربعة في أي مثلث متساوي الأضلاع. يمكن رسم مستقيم أويلر بإيجاد أي نقطتين من النقاط الأربعة والوصل بينهما.
من النقاط الأخرى التي تقع على مستقيم أويلر هي نقطة دي لونغشام، نقطة شيفلر، النقطة الخارجية، والنقطة البعيدة. ولكن مركز الدائرة المحاطة الداخلية يقع على مستقيم أويلر في المثلث المتساوي الساقين فقط.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
مراجع (لغة إنكليزية)
- Euler, Leonhard (1767). "Solutio facilis problematum quorundam geometricorum difficillimorum". Novi Commentarii academiae scientarum imperialis Petropolitanae. 11: 103–123. E325..
وصلات خارجية
 | هذه بذرة مقالة عن الهندسة الرياضية تحتاج للنمو والتحسين، ساهم في إثرائها بالمشاركة في تحريرها. |
