مسألة نابليون
في الهندسة الرياضية، مسألة نابليون هي مسألة مشهورة في إنشاءات الفرجار والمسطرة، حيث تنص، بافتراض دائرة ومركزها، المطلوب هو تقسيم الدائرة إلى أربع أقواس متساوية باستخدام الفرجار فقط.
من المعروف أن نابليون بونابرت كان من هواة الرياضيات، ولكن ليس من المؤكد من أنه صاغ أو حل هذه المسألة. صديق نابليون، عالم الرياضيات الإيطالي لورنزو ماسكروني قدّم قيداً هو استخدام الفرجار فقط (بدون مسطرة) إلى الإنشاءات الهندسية. إلا أنه في الواقع، فإن التحدي المذكور أعلاه يبدو بسيطاً إذا ما قورن بـ مسألة ناپليون الحقيقية، والتي تتكون من العثور على مركز دائرة معطاة، وذلك باستخدام الفرجار فقط. الأقسام التالية تصف حلاً لتلك المسألة، إثباتاً لنجاحها. گيورگ مور، في 1672، أصدر كتاب "Euclides Danicus"، الذي سبق ماسكروني، إلا أن الكتاب لم يُعـَد اكتشافه إلا في 1928.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
العثور على مركز دائرة معطاة
الإنشاء
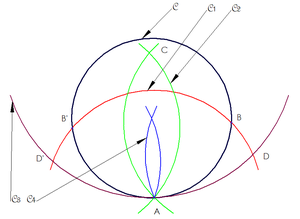
افترض أن (C) هي الدائرة التي نريد العثور على مركزها. وافترض أن A هي نقطة على (C).
A circle (C1) centered at A meets (C) at B and B'.
Two circles (C2) centered at B and B', with radius AB crosses again at point C.
A circle (C3) centered at C with radius AC meets (C1) at D and D'
Two circles (C4) centered at D and D' with radius AD meet at A، وعند المركز الذي نبحث عنه (C).
Note: for this to work the radius of circle (C1) must be neither too small nor too large. More precisely, this radius must be between half and double of the radius of (C).
البرهان
الفكرة وراء البرهان هي إنشاء، بالفرجار فقط، الطول b²/a عندما يكون الطولان a و b معروفين.
In the figure on the right, triangle ABA' has a right angle at B and BH is perpendicular to AA", so : AH/AB = AB/AA' ولذلك AH = b²/(2a) and AC = b²/a
في الإنشاء أعلاه، نشاهد مرتين هذا النوع :
- points A, B and B' are on the circle of centre O, radius r ; AB, AB', BC and B'C are equal to R, so
- points A, D and D' are on the circle of centre C, radius , DA, D'A, DX, D'X are equal to R so .
ولذلك X هي مركز الدائرة (C)
````
تقسيم دائرة معطاة إلى أربع أقواس متساوية بمعرفة مركزها
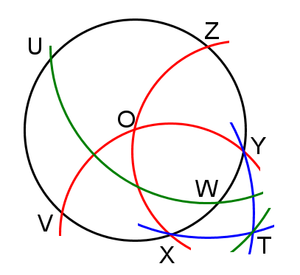
متمركزاً في أي نقطة X على الدائرة C، ارسم قوساً يمر بالنقطة O (مركز C) ويتقاطع مع C في النقطتين V و Y. افعل نفس الشيء متمركزاً في Y ماراً بالنقطة O، قاطعاً C في X و Z. لاحظ أن المسافات OV, OX, OY, OZ, VX, XY, YZ هم جميعاً نصف قطر الدائرة C.
Now draw an arc centred on V which goes through Y and an arc centred on Z which goes through X; call where these two arcs intersect T. Note that the distances VY and XZ are times the radius of the circle C.
Put the compass radius equal to the distance OT ( times the radius of the circle C) and draw an arc centred on Z which intersects the circle C at U and W. UVWZ is a square and the arcs of C UV, VW, WZ, and ZU يساوي كل منهم ربع محيط الدائرة C.
انظر أيضاً
الهامش