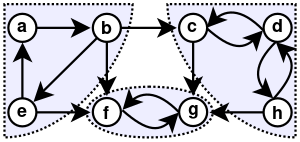
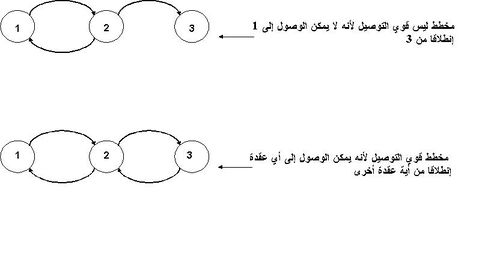
مخطط قوي التوصيل

Graph with strongly connected components marked

يقال أن مخطط (graph) ما قوي التوصيل (strongly connected)، إذا وجد مسلك أو طريق من كل عقدة في المخطط يوصل إلى أي نقطة أخرى. وإذا فسرنا ذلك من ناحية الرياضيات فإن هذه الخاصية تترجم بأن المصفوفة التابعة لهذا المخطط تكون غير قابلة للاختزال أي (irreducible) أي أن أي قوة للمصفوفة تعطيك مصفوفة ليست صفرا.

رسم توضيحي

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 التعريفات

A directed graph is called strongly connected if there is a path in each direction between each pair of vertices of the graph. That is, a path exists from the first vertex in the pair to the second, and another path exists from the second vertex to the first. In a directed graph G that may not itself be strongly connected, a pair of vertices u and v are said to be strongly connected to each other if there is a path in each direction between them.

The binary relation of being strongly connected is an equivalence relation, and the induced subgraphs of its equivalence classes are called strongly connected components. Equivalently, a strongly connected component of a directed graph G is a subgraph that is strongly connected, and is maximal with this property: no additional edges or vertices from G can be included in the subgraph without breaking its property of being strongly connected. The collection of strongly connected components forms a partition of the set of vertices of G. A strongly connected component $C$ is called trivial when $C$ consists of a single vertex which is not connected to itself with an edge and non-trivial otherwise.

The yellow directed acyclic graph is the condensation of the blue directed graph. It is formed by contracting each strongly connected component of the blue graph into a single yellow vertex.

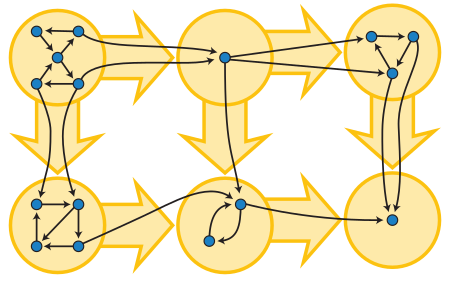
If each strongly connected component is contracted to a single vertex, the resulting graph is a directed acyclic graph, the condensation of G. A directed graph is acyclic if and only if it has no strongly connected subgraphs with more than one vertex, because a directed cycle is strongly connected and every non-trivial strongly connected component contains at least one directed cycle.

 الخوارزميات

 خوارزميات الزمن الخطي المبنية على DFS

Several algorithms based on depth first search compute strongly connected components in linear time.

 التطبيقات

Algorithms for finding strongly connected components may be used to solve 2-satisfiability problems (systems of Boolean variables with constraints on the values of pairs of variables): as Aspvall, Plass & Tarjan (1979) showed, a 2-satisfiability instance is unsatisfiable if and only if there is a variable v such that v and its complement are both contained in the same strongly connected component of the implication graph of the instance.

Strongly connected components are also used to compute the Dulmage–Mendelsohn decomposition, a classification of the edges of a bipartite graph, according to whether or not they can be part of a perfect matching in the graph.

 نتائج ذات صلة

A directed graph is strongly connected if and only if it has an ear decomposition, a partition of the edges into a sequence of directed paths and cycles such that the first subgraph in the sequence is a cycle, and each subsequent subgraph is either a cycle sharing one vertex with previous subgraphs, or a path sharing its two endpoints with previous subgraphs.

According to Robbins' theorem, an undirected graph may be oriented in such a way that it becomes strongly connected, if and only if it is 2-edge-connected. One way to prove this result is to find an ear decomposition of the underlying undirected graph and then orient each ear consistently.

 انظر أيضاً

• Clique (graph theory)
• Connected component (graph theory)
• Modular decomposition
• Weak component

 وصلات خارجية

• Java implementation for computation of strongly connected components in the jBPT library (see StronglyConnectedComponents class).
• C++ implementation of Strongly Connected Components