محاثة تبادلية

المحاثة التبادلية أو التحريض التبادلي (بالإنجليزية: Mutual Induction) ظاهرة تنشأ بين جزئين من الدائرة الكهربائية -ملفين عادة- عندما يحدث التغير في قيمة التيار الساري في أحداهما تحدث قوة دافعة كهربائية في الآخر. يولد التيار الموجود في إحدى الدائرتين مجالا مغناطيسيا يتغير بتغير التيار ويعترض الدائرة الأخرى. تنشأ بالحث القوة الكهربائية نتيجة الاتصال الموجود بين الدائرة الثانية وبين المجال المغنطيسي المتغير. تقاس المحاثة التبادلية بوحدة الهنري.

وهو حالة خاصة من ظاهرة التحريض الكهرمغنطيسي، والفرق بينهما هو أنه في ظاهرة التحريض الكهرمغنطيسي يكون تَغيُّر التدفق (الفيْض flux) المغنطيسي، عبْر سطح الدارة التي يتحرض فيها التيار الكهربائي، ناجماً عن مصدرٍ خارجي بالنسبة إلى الدارة، أما في ظاهرة التحريض الذاتي فإنّ تَغَيّر التدفق المغنطيسي عبْر سطح الدارة ينشأ عن تغير شدة التيار الكهربائي الذي يجتاز الدارة نفسها. فمثلاً، المِلَفُّ المجتاز بتيار، يتلقى تدفقاً مغنطيسياً f يُولِّده هذا التيار نفسُه. فإذا تغيرت شدة التيار، أو تَشَوَّه شكل الملف، تَغيََّر التدفق f وصار الملف مُسْتَقَرَّ قوة محركة كهربائية(ق م ك) تحريضية ذاتية es، يعطي قانون فارادي شدتها، فهي تساوي بالقدر مشتق التدفق (بالنسبة إلى الزمن t. أما إشارة الناقص فتُعبّر عن قانون لنز Lenz الذي ينص على أن es تسعى لمعاكسةِ تَغيُّرِ التيار، أو لمعاكسةِ تَشَوُّهِ الملف.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 المُحارَضَة (التحريضية أو معامل التحريض الذاتي inductance)

يمكن مقارنة التدفق f الذي تُولِّده وتتلقاه دارةٌ مّا، بشدة التيار الذي أدى إلى نشوئه. وتُحدِّد النسبةُ بينهما L، المسماةُ «مُحارَضَة» الدارة، أهمية التدفق الذي ترسله الدارةُ عبْر الدارة نفسِها، في حالة تيار معيَّن. إن المقدار L موجب دوماً، ويكون ثابتَ القيمة إذا كانت الدارة صلبةً (غير قابلة للتشوه) وموضوعةً في وَسَطٍ مغنطيسي ذي نفوذية (نفاذية permeability) ثابتة، ذلك لأن التدفق يتناسب عندئذ مع التيار. أما إذا كانت الدارة ليّنة (قابلة للتشوه) أو موضوعة في وسطٍ حديديّ التمغْنط ferromagnetic فإن L يكون متغيراً، وهذه حالة ملفٍ ذي نواة (قَلْبٍ core) حديدية.

تسمح العلاقة بين تغير شدة التيار والقوة المحركة الكهربائية الناتجة عنها تعريف وحدة قياس المحارضة في النظام (الجملة) الدولي SI للوحدات، وهي الهنري henri، ورمزها H، إذ تكون محارضة الدارة المغلقة مساوية 1H إذا تحرضت فيها ق م ك قدرها فُلْط واحد 1V عندما يتغير التيار الكهربائي الذي يجتازها تغيراً منتظماً بمعدل أمبير واحد 1A في الثانية. وهذا يكافئ القول: إن هذه الدارة تتلقى تدفقاً قدره فيبر واحد 1W عندما يجتازها تيار شدته أمبير واحد.

 تعيين فيمة المحارضات

يمكن، في عدد من الحالات، حساب محارضة الملف انطلاقاً من شكله الهندسي وعدد لفّاته؛ وهناك كُتيّبات مخصصة لهذا الحساب؛ ويلاحظ فيها أن المحارضة تتناسب مع مربع عدد اللفات. فمثلاً، في حالة ملف بلا تَسَرُّبٍ مغنطيسي (وذلك عندما يتلقى جميعُ اللفّات خطوط تدفقٍ واحدة) تكون عبارة المحارضة: L = N2/R حيث N عدد اللفّات، وR هي الممانعة المغنطيسية reluctance التي تُبديها الدارة لمجموعة خطوط التدفق.

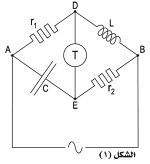
وفي معظم الحالات تُعيَّن المحارضة بالقياس. وثمة طرائق عديدة لتنفيذ ذلك، أهمها استعمال التجاوب resonance الكهربائي وجُسور المُعاوَقات impedance كجسر ويتسطن. يستعمل هذا الجسر إذا كان الملف المراد قياس محارضته L عديم المقاومة الأومية r = 0. وهذا مستحيل عملياً، إنما يمكن أن تكون r صغيرة جداً إزاء Lw حيث w نبض التيار المتناوب الذي يغذي الجسر. وتُختار المقاومتان r1 و r2 بحيث ينعدم فرق الكمون(الجهد) بين طرفي الجسر E ، D ـ ومن ثّم ينعدم التيار في الكاشف الصِّفريّ T (سمّاعة هاتف مثلاً، فينعدم فيها الصوت أو تبلغ شدته حداً أدنى). ويقال عندئذ إن الجسر متوازن ـ وتتحقق آنئذ العلاقة L = C r1 r2 التي تعطي قيمة المحارضة المجهولة بدلالة سعة المكثفة C والمقاومتين r1 و r2.

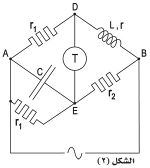
أما إذا كانت مقاومة الملف r غير مهملة، فيُستعمل جسر مكسويل، الذي يختلف عن جسر ويتسطن بوصل مقاومة r1 على التفرع مع المكثفة. ولِتَوازن جسر مكسويل شرطان هما:

r1 r2 = r r1 = L /C ومن أحدهما تُحسب L.

وعند وصل مِلَفَّين على التسلسل تكون المحارضة الكلية مساوية:

L = L1 + L2 2M

حيث L1 و L2 محارضتا الملفين على الترتيب، وM معامل التحريض المتبادل، وتتوقف قيمته على الوضع النسبي للملفين. فإذا كان هذا الوضع قابلاً للتغيير أمكن الحصول على محارضة كلية متغيرة (قابلة للتعديل) تقع قيمتها بين: L1 + L2 + 2M و L1 + L2 2M

 تأثير التحريض الذاتي عند إغلاق الدارة الكهربائية وفتحها

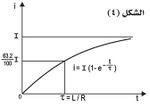
1 ـ إغلاق الدارة: إذا أغلقت دارةٌ، مقاومتها الكلية R ومحارضتها الثابتة L، على ق م ك مستمرة(متواصلة) قيمتها e، فإن شدة التيار تكون متغيرة، فلا تقفز الشدة فجأة من الصفر إلى القيمة النهائية I = e / R التي يقتضيها قانون أوم، وإنما تتغير، بَدءاً من لحظة الإغلاق t = 0، وفق منحنى بياني.

فالقوة المحركة الكهربائية التحريضية الذاتية تَوَطُّد التيار الذي يستغرق، نظرياً، زمناً لانهائياً ليبلغ قيمته النهائية I. وكلما صَغُر المقدار المسمى «الثابتة الزمنية» زادت سرعة اقتراب i من I لأن:

ففي اللحظة تكون النسبة i/I مساوية:

وفي اللحظة تكون النسبة i/I مساوية:

وفي اللحظة تكون النسبة i/I مساوية:

ويُستنتج الميزان الطاقيّ بالمكاملة فنجد: a = b + c

حيث يمثِل المقدار a الطاقة الكلية التي يقدمها المولد. ويمثل المقدار b الطاقة المتبددة بفعل جول. أما المقدار c فيمثل الطاقة الكهرمغنطيسية المختزنة في الملف.

2 ـ فَتْح الدارة: عند فتح الدارة يكوِّن مربطا القاطعة مكثفة بعيدة جداً من الكمال. وبسبب تلاشي التيار تتحول الطاقة الكهرمغنطيسية المختزنة إلى طاقة كهراكدية electrostatic . ويمكن أن تكون c، وهي سعة القاطعة، صغيرة جداً، ومن ثَم يمكن أن يصير فرق الكمون U بين مربطيها كبيراً فيُسبّب انقداح قوسٍ كهربائية تسمى «شرارة الانقطاع». ولهذه الظاهرة محاذير منها: انثقاب العوازل، وتَلَفُ مرابط القواطع، وخطر الانصعاق بالكهرباء، وإصدار موجات كهرمغنطيسية (تشويش الاتصالات الراديوية). ويمكن معالجة الأمر بوصل مكثفة كبيرة السعة إلى مربطي القاطعة، أو بوضع مقاومة على التفرع (التوازي) مع الملف في لحظة فتْح الدارة.