متباينة المثلث

Three examples of the triangle inequality for triangles with sides of lengths

x

,

y

,

z

. The top example shows a case where

z

is much less than the sum

x + y

of the other two sides, and the bottom example shows a case where the side

z

is only slightly less than

x + y

.

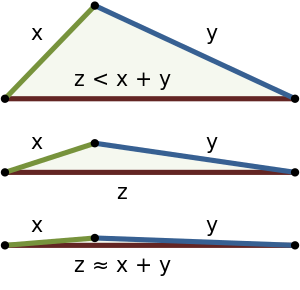
لامساواة المثلث أو متراجحة المثلث هي المتراجحة الشهيرة التي تقول أن طول أي ضلع من اضلاع المثلث أصغر حتما من مجموع الضلعين الأخريين و أكبر حتماً من فرقهما.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

الهندسة الإقليدية

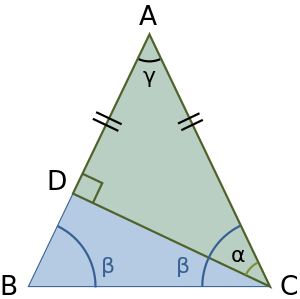
Euclid's construction for proof of the triangle inequality for plane geometry.

المثلث القائم

Isosceles triangle with equal sides

AB = AC

divided into two right triangles by an altitude drawn from one of the two base angles.

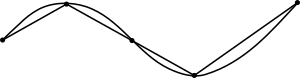
العلاقات بين أقصر الطرق

The arc length of a curve is defined as the least upper bound of the lengths of polygonal approximations.

This generalization can be used to prove that the shortest curve between two points in Euclidean geometry is a straight line.

انظر أيضاً

الهامش

المراجع

Pedoe, Daniel (1988). Geometry: A comprehensive course. Dover. ISBN 0-486-65812-0..
Rudin, Walter (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. ISBN 0-07-054235-X..

وصلات خارجية

قالب:ProofWiki