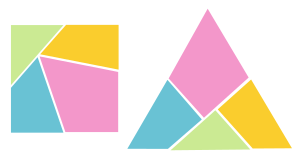مبرهنة والاس-بولياي-گرڤين

حسب مبرهنة والاس-بولياي-گرڤين، فإن مربعاً يمكن تقطيعه إلى أجزاء ويعاد ترتيبه إلى مثلث بنفس المساحة.

في الهندسة الرياضية، مبرهنة والاس-بولياي-گرڤين (إنگليزية: Wallace–Bolyai–Gerwien theorem) تنص على أنه إذا وجد مضلعين بسيطين لهما مساحة متساوية، من الممكن تقسيم المضلع الأول إلى عدد نهائي من المضلعات الصغيرة وإعادة ترتيبها للحصول على المضلع الثاني.

"إعادة الترتيب" هنا تعني أنه من الممكن إجراء نقل و دوران على كل القطع الصغيرة.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 التاريخ

فاركاس بولياي صاغ المسألة لأول مرة. گرڤين أثبت المبرهنة في 1833، ولكن في الواقع والاس كان قد أثبت نفس النتيجة بالفعل في 1807.

وحسب مصادر أخرى، فإن بولياي وگرڤين قد أثبت كل منهما المبرهنة بشكل مستقل عن الآخر في عامي 1833 و 1835، بالترتيب.

 درجة قابلية التفكيك

Consider two equidecomposable polygons P and Q. The minimum number n of pieces required to compose one polygon Q from another polygon P is denoted by σ(P,Q).

Depending on the polygons, it is possible to estimate upper and lower bounds for σ(P,Q). For instance, Alfred Tarski proved that if P is convex and the diameters of P and Q are respectively given by d(P) and d(Q), then

$\sigma (P,Q)\geq {\frac {d(P)}{d(Q)}}.$

If P_x is a rectangle of sides a·x and a·(1/x) and Q is a rectangle of size a, then P_x and Q are equidecomposable for every x > 0. An upper bound for σ(P_x,Q) is given by

$\sigma (P_{x},Q)\leq 2+\left\lceil {\sqrt {x^{2}-1}}\right\rceil ,\quad {\text{for }}x\geq 1$

Since σ(P_x,Q) = σ(P_(1/x),Q), we also have that

$\sigma \left(P_{\frac {1}{x}},Q\right)\leq 2+\left\lceil {\frac {\sqrt {1-x^{2}}}{x}}\right\rceil ,\quad {\text{for }}x\leq 1$

 التعميمات: الأبعاد الأعلى

تعميم هذه المبرهنة على متعددات الأوجه في الفضاء ثلاثي الأبعاد تعرف باسم مسألة هلبرت الثالثة وهي عبارة خاطئة وقد تم برهان خطئها من قبل ماكس دين في عام 1900.

 وصلات خارجية

• Wallace–Bolyai–Gerwien Theorem
• Scissors Congruence - An interactive demonstration of the Wallace–Bolyai–Gerwien theorem.
• Video showing a sketch of the proof
• An Example of the Bolyai–Gerwien Theorem by Sándor Kabai, Ferenc Holló Szabó, and Lajos Szilassi, the Wolfram Demonstrations Project.
• A presentation about Hilbert's third problem at College of Staten Island CUNY - Abhijit Champanerkar.
• Optimal dissection of a unit square in a rectangle