مبرهنة كارنو

${\begin{aligned}&{}\qquad DG+DH+DF\\&{}=|DG|+|DH|-|DF|\\&{}=R+r\end{aligned}}$

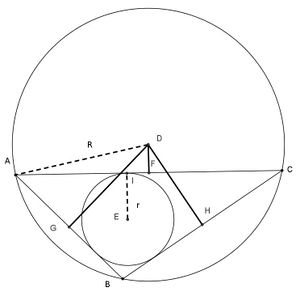
في الهندسة الإقليدية، تنص مبرهنة كارنو التي سميت على اسم لازار كارنو (1753 - 1823) مايلي: هب أن ABC مثلث ما، فإن مجموع المسافات من الدائرة المحيطة D إلى أضلاع المثلث ABC تحقق العلاقة:

DF + DG + DH = R + r,

حيث r نصف القطر الدائرة المحاطة، R نصف قطر الدائرة المحيطة. وتأخذ إشارة المسافة على أنها سالبة إذا كانت القطعة المستقيمة DX (X = F, G, H) تقع بكاملها خارج المثلث. حيث في الصورة الموضحة القطعة المستقيمة DF تكون ذات طول سالب، والقطعتين المستقيمتين DGو DH موجبتان.

تستخدم مبرهنة كارنو في برهان مبرهنة يابانية في مضلع دائري.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 وصلات خارجية

• Eric W. Weisstein, مبرهنة كارنوت at MathWorld.