مبرهنة ديسارگو

The Desargues configuration viewed as a pair of mutually inscribed pentagons: each pentagon vertex lies on the line through one of the sides of the other pentagon.

مبرهنة ديسارگو هي مبرهنة في هندسة الإسقاط، سميت على اسم العالم جيرار ديسارگو، نصها كما يلي:

في فضاء الإسقاط، يكون مثلثان منظوران محورياً إذا وفقط إذا كانا منظوران مركزياً.

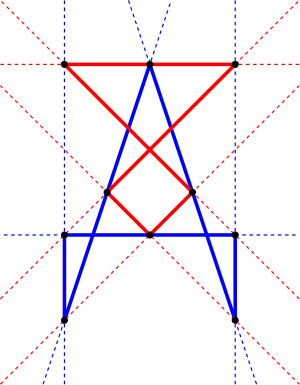
من أجل فهم المبرهنة، ليكن لدينا ثلاث نقاط على مثلث ما (نرمز لها بأحرف صغيرة a, b, c) وثلاث نقاط على مثلث آخر (بأحرف كبيرة A, B, C). إن المنظورية المحورية تكون محققة إذا وفقط إذا كانت نقط تقاطع امتداد اضلع المثلثين , مثلاً تقاطع ab مع AB و ac مع AC و bc مع BC , ينتمون الى نفس الخط الذي يدعى محور المنظورية. وتتحقق المنظورية المركزية إذا وفقط إذا تقاطعت المستقيمات Aa، Bb، Cc في نقطة واحدة هي مركز المنظور.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 انظر ايضاً

• تماثل

 المصادر

• Coxeter, Harold Scott MacDonald (1969), Introduction to Geometry (2nd ed.), New York: John Wiley & Sons, قالب:MR, ISBN 978-0-471-50458-0 
• Hilbert, David; Cohn-Vossen, Stephan (1952). Geometry and the Imagination (2nd ed. ed.). Chelsea. pp. 119–128. ISBN 0-8284-1087-9. {{cite book}}: |edition= has extra text (help)CS1 maint: multiple names: authors list (link)
• Hessenberg, Gerhard (1905), "Beweis des Desarguesschen Satzes aus dem Pascalschen", Mathematische Annalen (Berlin / Heidelberg: Springer) 61 (2): 161-172, doi:10.1007/BF01457558, ISSN 1432-1807 
• قالب:Eom

 وصلات خارجية

• Desargues Theorem at MathWorld
• Desargues' Theorem at cut-the-knot
• Monge via Desargues at cut-the-knot
• Alternate proof of Desargues' theorem at PlanetMath