كرة داخلية
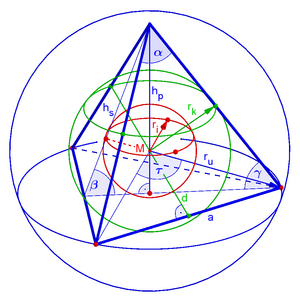

في الهندسة الرياضية، تعرف الكرة الداخلية في مجسم محدب على أنها الكرة التي تُحتوي بكاملها في هذا المجسم وتكون مماسة لكل وجه من أوجه المجسم. وهي أكبر كرة من الممكن احتوائها ضمن المجسم. لجميع المجسمات المنتظمة كرات داخلية تمس جميع أوجهها، ولكن بعض المجسمات الغير منتظمة لا تمس الكرة جميع أوجهها الداخلية ولكن يبقى تعريف أكبر كرة داخلية ممكناً.
The radius of the sphere inscribed in a polyhedron P is called the inradius of P.
Interpretations
All regular polyhedra have inscribed spheres, but most irregular polyhedra do not have all facets tangent to a common sphere, although it is still possible to define the largest contained sphere for such shapes. For such cases, the notion of an insphere does not seem to have been properly defined and various interpretations of an insphere are to be found:
- The sphere tangent to all faces (if one exists).
- The sphere tangent to all face planes (if one exists).
- The sphere tangent to a given set of faces (if one exists).
- The largest sphere that can fit inside the polyhedron.
Often these spheres coincide, leading to confusion as to exactly what properties define the insphere for polyhedra where they do not coincide.
For example, the regular small stellated dodecahedron has a sphere tangent to all faces, while a larger sphere can still be fitted inside the polyhedron. Which is the insphere? Important authorities such as Coxeter or Cundy & Rollett are clear enough that the face-tangent sphere is the insphere. Again, such authorities agree that the Archimedean polyhedra (having regular faces and equivalent vertices) have no inspheres while the Archimedean dual or Catalan polyhedra do have inspheres. But many authors fail to respect such distinctions and assume other definitions for the 'inspheres' of their polyhedra.
انظر أيضاً
المراجع
- Coxeter, H.S.M. Regular Polytopes 3rd Edn. Dover (1973).
- Cundy, H.M. and Rollett, A.P. Mathematical Models, 2nd Edn. OUP (1961).
وصلات خارجية