فاصل دوامي

A simple cyclone separator

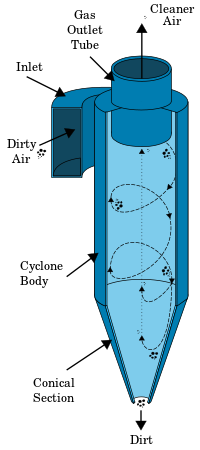
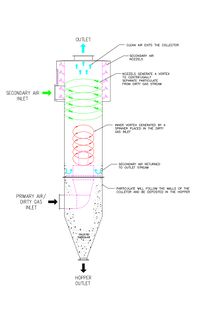
الفاصل الدوامي أو الفرازة الدوارة Cyclonic separation جهاز يفصل الشوائب (Particulates) عن تيار مائع (هوائي أو غازي أو سائل) بدون استخدام مرشحات، ويستغل ظاهرة الدوامة. يستغل الجهاز تأثيرات الدوران والجاذبية لفصل الصلب عن المائع. ويمكن لهذه طريقة أيضا أن تفصل قطيرات السائل عن تيار غازي.

Airflow diagram for Aerodyne cyclone in standard vertical position. Secondary air flow is injected to reduce wall abrasion.

Airflow diagram for Aerodyne cyclone in horizontal position, an alternate design. Secondary air flow is injected to reduce wall abrasion, and to help move collected particulates to hopper for extraction.

Assuming Stokes' law, the drag force in the outward radial direction that is opposing the outward velocity on any particle in the inlet stream is:

$F_{d}=-6\pi r_{p}\mu V_{r}.$

Using $\rho _{p}$ as the particles density, the centrifugal component in the outward radial direction is:

$F_{c}=m{\frac {V_{t}^{2}}{r}}$

$={\frac {4}{3}}\pi \rho _{p}r_{p}^{3}{\frac {V_{t}^{2}}{r}}.$

The buoyant force component is in the inward radial direction. It is in the opposite direction to the particle's centrifugal force because it is on a volume of fluid that is missing compared to the surrounding fluid. Using $\rho _{f}$ for the density of the fluid, the buoyant force is:

$F_{b}=-V_{p}\rho _{f}{\frac {V_{t}^{2}}{r}}$

$=-{\frac {4\pi r_{p}^{3}}{3}}{\frac {V_{t}^{2}}{r}}\rho _{f}.$

In this case, $V_{p}$ is equal to the volume of the particle (as opposed to the velocity). Determining the outward radial motion of each particle is found by setting Newton's second law of motion equal to the sum of these forces:

$m{\frac {dV_{r}}{dt}}=F_{d}+F_{c}+F_{b}$

To simplify this, we can assume the particle under consideration has reached "terminal velocity", i.e., that its acceleration ${\frac {dV_{r}}{dt}}$ is zero. This occurs when the radial velocity has caused enough drag force to counter the centrifugal and buoyancy forces. This simplification changes our equation to:

$F_{d}+F_{c}+F_{b}=0$

Which expands to:

$-6\pi r_{p}\mu V_{r}+{\frac {4}{3}}\pi r_{p}^{3}{\frac {V_{t}^{2}}{r}}\rho _{p}-{\frac {4}{3}}\pi r_{p}^{3}{\frac {V_{t}^{2}}{r}}\rho _{f}=0$

Solving for $V_{r}$ we have

$V_{r}={\frac {2}{9}}{\frac {r_{p}^{2}}{\mu }}{\frac {V_{t}^{2}}{r}}(\rho _{p}-\rho _{f})$.

Notice that if the density of the fluid is greater than the density of the particle, the motion is (-), toward the center of rotation and if the particle is denser than the fluid, the motion is (+), away from the center. In most cases, this solution is used as guidance in designing a separator, while actual performance is evaluated and modified empirically.

In non-equilibrium conditions when radial acceleration is not zero, the general equation from above must be solved. Rearranging terms we obtain

${\frac {dV_{r}}{dt}}+{\frac {9}{2}}{\frac {\mu }{\rho _{p}r_{p}^{2}}}V_{r}-\left(1-{\frac {\rho _{f}}{\rho _{p}}}\right){\frac {V_{t}^{2}}{r}}=0$

Since $V_{r}$ is distance per time, this is a 2nd order differential equation of the form $x''+c_{1}x'+c_{2}=0$.

Experimentally it is found that the velocity component of rotational flow is proportional to $r^{2}$, therefore:

$V_{t}\propto r^{2}.$

This means that the established feed velocity controls the vortex rate inside the cyclone, and the velocity at an arbitrary radius is therefore:

$U_{r}=U_{in}{\frac {r}{R_{in}}}.$

Subsequently, given a value for $V_{t}$, possibly based upon the injection angle, and a cutoff radius, a characteristic particle filtering radius can be estimated, above which particles will be removed from the gas stream.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 انظر أيضا

• دوامية
• عمليات فصل