ظل (رياضيات)
ظل الزاويه يُعرف بأنه النسبه بين الجيب وجيب التمام لنفس الزاويه.
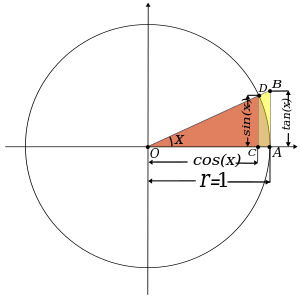
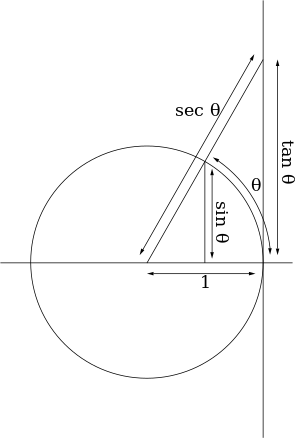
اذا نظرنا إلى صورة (1)، نرى ان المثلثات oab و OCD مماثلة، لذلك لذي ينطوي على العلاقة الاساسية بين الظل، الجيب وجيب التمام :
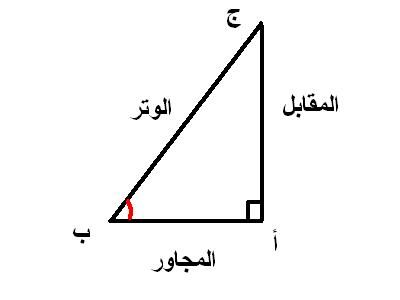
حساب الظل: في مثلث قائم الظل يساوي طول الضلع المقابل/طول الضلع المجاور
كما أن : ظل=جب/نجب مثال:
مثلا: طول الضلع [أج] =15سنتمتر
طول الضلع [أب] =05سنتمتر
طول الضلع [ج ب] (الوتر) =19سنتمتر
لحساب ظل(tan) الزاوية ب :
المقابل [أج] / المجاور [أب]
33 / 05 = 3
إذن: ظل(tan) الزاوية ب هو: 5
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
التاريخ
| Function | Abbreviation | Identities (using radians) |
|---|---|---|
| Sine | sin | |
| Cosine | cos | |
| Tangent | tan (or tg) |
|
| Cosecant | csc (or cosec) |
|
| Secant | sec | |
| Cotangent | cot (or ctg or ctn) |
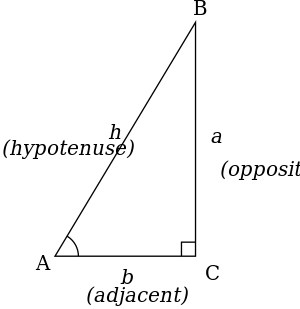
Right triangle definitions
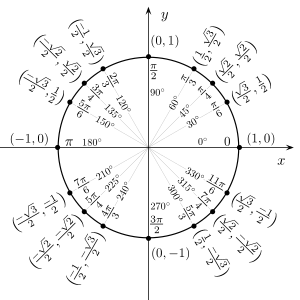
بعض الزوايا الشهيرة
- [إعجاز القرآن الكريم في وصف حركة الظلال http://www.nooran.org/con8/Research/8.pdf]
- ظل0=0
- ظل90=عدم تعيين
- ظل180=0
- ظل270=عدم تعيين
انظر أيضا
- Generating trigonometric tables
- Hyperbolic function
- Pythagorean theorem
- Unit vector (explains direction cosines)
- Table of Newtonian series
- List of trigonometric identities
- Proofs of trigonometric identities
- Euler's formula
- Polar sine — a generalization to vertex angles
- All Students Take Calculus — a mnemonic for recalling the signs of trigonometric functions in a particular quadrant of a Cartesian plane
- Continued fraction of Gauss — a continued fraction definition for the tangent function
وصلات خارجية
- Visionlearning Module on Wave Mathematics
- GonioLab: Visualization of the unit circle, trigonometric and hyperbolic functions
- Dave's draggable diagram. (Requires java browser plugin)
المصادر
- Abramowitz, Milton and Irene A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Dover, New York. (1964). ISBN 0-486-61272-4.
- Boyer, Carl B., A History of Mathematics, John Wiley & Sons, Inc., 2nd edition. (1991). ISBN 0-471-54397-7.
- Joseph, George G., The Crest of the Peacock: Non-European Roots of Mathematics, 2nd ed. Penguin Books, London. (2000). ISBN 0-691-00659-8.
- Kantabutra, Vitit, "On hardware for computing exponential and trigonometric functions," IEEE Trans. Computers 45 (3), 328–339 (1996).
- Maor, Eli, Trigonometric Delights, Princeton Univ. Press. (1998). Reprint edition (February 25, 2002): ISBN 0-691-09541-8.
- Needham, Tristan, "Preface"" to Visual Complex Analysis. Oxford University Press, (1999). ISBN 0-19-853446-9.
- O'Connor, J.J., and E.F. Robertson, "Trigonometric functions", MacTutor History of Mathematics Archive. (1996).
- O'Connor, J.J., and E.F. Robertson, "Madhava of Sangamagramma", MacTutor History of Mathematics Archive. (2000).
- Pearce, Ian G., "Madhava of Sangamagramma", MacTutor History of Mathematics Archive. (2002).
- Weisstein, Eric W., "Tangent" from MathWorld, accessed 21 January 2006.