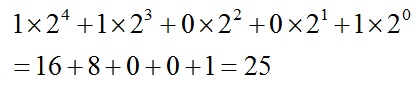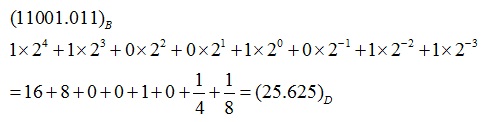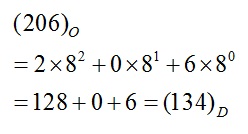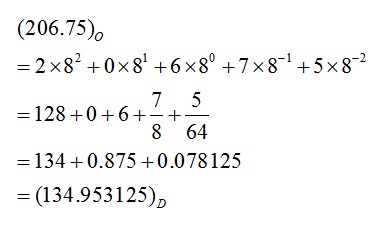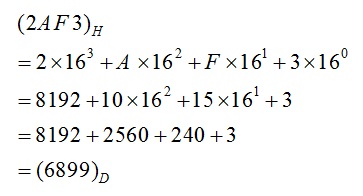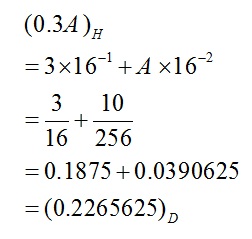طرق التحويل بين أنظمة العد

- تعريف نظام العد هو نظامٌ لتمثيل الأعداد (بالإنجليزية: Numeral system:

ويُشكل نظامُ العدّ البنية الحسابيّة والجبريّة للأعداد، حيث يَسمح لنا بإجراء العمليّات الحسابيّة اللاّزمة كالجمع والطرح، والقسمة والضرب.
ويمكن تعريفه أيضًا بأنّه مجموعةٌ من الرُّموزالمُستخدمة لتمثيل أعدادٍ صغيرة، أو اتّحاد مجموعةٍ من الرموز مع أنظمة القواعد لتمثيل أعداد أكبر.

ومن خصائص أنظمة العد إمكانية استخدامها لتشكيل أرقام تمثل أرقامًا مختلفة في أنظمة عدّ مختلفة، فعلى سبيل المثال، يُمثل الرقم 11 المُستخدم في نظام الأرقام العشري الرقم 3 في نظام الأرقام الثنائية المُستخدم في أجهزة الحاسوب. - سبب تنوع أنظمة العد

يعود السّبب الأساسيّ لتنوُّع أنظمة العد هو تنوُّع الاستخدامات والمجالات التي أظهرت حاجةً ملحةً لتمثيل جميع الأرقام، واستخدامها لحلّ سلسلة من المسائل الرياضية التي قد تُواجهنا يومًا بعد يوم، كالنّظام العشري، والثنائيّ، والثّماني، والسداسي عشري، وبسبب أهمية أنظمة العد وتنوعها، فإنّ تعلم طرق التّحويل بين أنظمة العد أصبح ضروريًا.[٥] نظام العد الثنائي نظام العد الثنائي (بالإنجليزية: Binary Numeral System) هو أحد أنظمة العدّ وأساسه الرّقم 2، وهو مُشابه من حيث المبدأ لنظام العد العشري، الذي نستخدمه في حياتنا اليومية، ويُستخدم لتمثيل الأرقام باستخدام رمزين هما: 0 و1، حيث يُستخدم النظام الثنائي في أجهزة الحواسيب، ومن الجدير بالذّكر أنّه نظام العدّ الوحيد الذي تستخدمه وتتواصل به أجهزة الحاسوب.

-مُميّزات نظام العد الثنائيّ: من مميزات نظام العد الثنائي ما يأتي: يتميز النظام الثنائي بسهولة المعالجة؛ نظرًا لأنه يتكون من الرّقمين 0 و1 فقط.

يتميز بأنّ أساسه الرقم 2.
يمتلك كل رقم في هذه النظام قيمةً مختلفة باختلاف موقعه.
يُستخدم النظام الثنائي في جميع أجهزة الحاسوب.

-عيوب نظام العد الثنائي

من عيوب نظام العد الثنائي ما يأتي:
يُعدُّ العيب الرئيسيّ لنظام العد الثنائي هو صعوبة قراءته وكتابته بالنّسبة للبشر.
يُعدُّ تخزين أي رقم ثنائي مهمة صعبة جدًا؛ ويرجع ذلك إلى أنّ المُعالج يقومُ بتحويل كل حرف أو رقم إلى سلسلة من الأرقام الثنائية، فعلى سبيل المثال، إذا كان لدينا نص مكوَّن من سبعة حروف، فسيتم تحويلها في النظام الثنائي كالآتي: (01100101 01111000 01100001 01101101 01110000 01101100 01100101).
يحتاج نظام العدّ الثنائيّ مساحة كبيرة للتخزين؛ مما يجعل عملية معالجة الأرقام الثنائية تستغرقُ وقتًا طويلًا.

-استخدامات نظام العد الثنائي هناك عدة استخدامات لنظام العد الثنائي، وهي كالآتي:

يُستخدم نظام العد الثنائي لتخزين ومعالجة جميع البيانات الرّقميّة (بالإنجليزية: Digital Data) في أجهزة الحاسوب أو أيّ جهازٍ رقميّ؛ سواءً كانت أرقامًا، كلمات، مقاطعَ الفيديو، رسومات، أو موسيقى.
يُستخدم هذا النّظام لحفظ كلمات المرور وتخزين البيانات الخاصّة بالمُستَخدمين , وذلك لجعل مواقع الويب أكثر أمانًا، ويرجع السبب في ذلك إلى صعوبة قراءة هذه الأرقام بالنسبة للمُخترقين، إذ إنهم في البدايةً يجب أن يحوّلوا الرّموز الثنائية إلى نصٍّ، حتى يتمكّنوا من قراءة كلمة المرور، وهذه العملية تسغرق وقتًا طويلًا، ممّا يُقلل فرص حدوث الاختراق.
يُستخدم النظام الثنائي في الدارّات الكهربائية؛ ويرجع السبب في ذلك إلى أن النظام الثنائي يستطيع تمثيل حالتي الدارّة الكهربائية سواء كانت مغلقة أو مفتوحة، وذلك من خلال استخدام رمزية وهما (0 , 1)، حيث يُمثل 0 دارّة كهربائية مفتوحة، بينما الرقم 1 يمثل دارّة كهربائية مغلقة.

- نظام العد العشري نظام العد العشري (بالإنجليزية: Decimal Numeral System)، هو أحد أنظمة العدّ، ويسمى بنظام الأرقام الهندوسيّة العربيّة أو نظام الأرقام العربية، ويستخدم الرقم 10 كأساس له، ويتكون هذا النظام من 10 أرقامٍ مختلفة، حيث يستخدم الأرقام (0 ، 1 ، 2 ، 3 ، 4 ، 5 ، 6 ، 7 ، 8 ، 9)، كما يتطلب وجودَ فاصلةٍ عشرية؛ في حال وجود الكسورالعشرية. مميزات نظام العد العشري من مميزات نظام العد العشري ما يأتي: يتميز نظام العد العشري بأنه سهل القراءة، والفهم والاستخدام، والتّطبيق للبشر في حياتهم ومُعاملاتهم. يُستخدم نظام العد العشري للقياس بشكل أكثر دقة، عن طريق إنشاء وحدات أصغر باستخدام الفاصلة العشرية؛ أيّ أنّ الكسور العشريّة تزيد من دقّة القياس في حالة وُجودها .

يُستخدم نظام العد العشري بكثرة في الأنظمة المضمّنة (بالإنجليزية: Embedded Systems).

ويقصد بالأنظمة المضمنة هي أنظمة لأجهزة الحاسوب تعتمد بشكل أساسي على المعالجات الدقيقة، أو التحكم الدقيق في الأجهزة والبرامج المصممة؛ لأداء وظائف معينة داخل نظام ميكانيكي أو كهربائي أكبر.

- عيوب نظام العد العشري

من عيوب نظام العد العشري ما يأتي:
يحتوي النظام العشري على 13 رمزًا؛ الأرقام من (0 إلى 9) وإشارة الجمع (+)، وإشارة الطّرح (-)؛ مما يجعل النّظام العشريّ صعبًا إلى حدّ كبير لتمثيل الأحرف أو عناوين الأجهزة الرقمية، أو أوامر وحدة المعالجة المركزية. يحجز النظام العشري مساحةً تخزينيةً كبيرةً من المعالج، وترجمته للغة الثنائيّة تتطلب وقتًا طويلًا , إذ إن كلّ رقم عشريّ لكي يُخزن في أجهزة الكمبيوتر، يتم تحويله أوّلاً إلى رقم ثنائيّ، ويحجز كل بت (بالإنجليزية: Bit)، ويحتاج كل بت واحد من النّظام العشريّ إلى مساحة تبلغ 4 بت من النّظام الثّنائيّ، إذ إنّ البت هي أصغر وحدة تخزين مُستخدمة في النّظام الرّقميّ.

- نظام العد الثماني

نظام العد الثماني (بالإنجليزية: Octal Numeral System)، هو أحد أنظمة العدّ وأساسه الرقم 8، ويستخدم هذا النظام الأرقام من 0 إلى 7، ويتطلّب هذا النّظام مساحةً تُقدَّر بثلاثة بتات (بالإنجليزية: Bits) لتمثيل قيمة أي رقم

- مميزات نظام العد الثماني ومن مميزات نظام العد الثماني ما يأتي:

استخدام عدد خانات أقلّ من النّظام العشري والسداسي العشري؛ الأمر الذي أدّى إلى قلّة عدد عملياته الحسابية، إضافةً إلى قِلة أخطائه الحسابيّة.
استخدام ثلاثة بتات، لتمثيل أيّ رقم في النّظام الثنائيّ.
سهولة تحويله إلى النظام الثنائي. من أكثر الأنظمة سهولةً في التّعامل مع المُدخلات والمُخرجات.

- عيوب نظام العد الثماني

ومن عيوب نظام العد الثماني ما يأتي :

- عدم مقدرة الحاسوب أو الأجهزة الرقمية على فهم نظام العد الثماني بصورة مباشرة، إذ يتوجّب التّحويل من نظام العدّ الثمانيّ إلى نظام العدّ الثنائيّ. - عدم سهولة تحويل نظام العد الثماني إلى أنظمة العد الأخرى، حيث عند تحويله إلى نظام العد السّداسي عشري، لا بدّ من تحويله أولًا إلى رقم عشريّ، ثمّ تحويله إلى رقم سداسي عشري.

- استخدامات نظام العد الثماني ومن أهم استخدامات نظام العد الثماني ما يأتي:[٣٠] يُستخدم نظام العد الثماني في تطبيقات الحاسوب. - يُستخدم نظام العد الثماني في نطاق الأنظمة الرقمية. - يُستخدم نظام العد الثماني في أنظمة الحوسبة. - يُستخدم نظام العد الثماني أيضًا في قطاع الطيران. - يُستخدم نظام العد الثماني في تحويل البتات (بالإنجليزية: Bits) بكلّ سهولة.

- نظام العد السداسي عشري

نظام العد السداسي عشري (بالإنجليزية: Hexadecimal)، هو أحد أنظمة العدّ وأساسه الرقم 16، ويُعبِّر نظام العد السداسي عشري عن نظام ترقيم يحتوي على 16 رقمًا، إذ يَستخدم هذا النّظام الأرقام من 0 إلى 9، والحروف من A إلى F.

- مميزات نظام العد السداسي عشري

ومن مميزات نظام العد السداسي عشري ما يأتي:
يَستخدم نظام العد السُّداسي العشري 10 أرقام، و6 حروف، وهي الأرقام: (0،1،2،3،4،5،6،7،8،9) أمّا الحروف فهي: (A,B,C,D,E,F) . تُمثِّل جميع الأحرف أرقامًا كما هو موضّح بين الأقواس (A=10, B=11, C=12, D=13, E=14, F=15). يُعدّ رقم الأساس للنّظام هو 16. يُعدّ النظام السداسي العشري فعَّالًا في ضغط البيانات؛ لأنه يستخدم رقم ست عشري واحد من (0-15)، على عكس نظام العد الثنائي الذي يستخدم رقمين للتّعبيرعن رقم واحد (0,1).[٣٣] يسهل تحويل البت (بالإنجليزية: Bit) إلى بايت (بالإنجليزية: Byte)، ويتم ذلك باستخدام نظام العدّ السداسي عشري.

- عيوب نظام العد السداسي عشري من عيوب نظام العد السداسي عشري ما يأتي: - يحتل هذا النظام مساحة أكبرعلى المعالج نظرًا إلى أنّ عدد عناصره 16 عنصرًا، وأساسه الرّقم 16. - قد تحدث مشكلات في الذّاكرة في بعض الأجهزة ذات الذّاكرة الصّغيرة، في حال استخدام هذا النّظام. - يُعدّ نظامًا غير سهل للقراءة أو الكتابة بالنسبة للبشر. - يُعدّ إجراء العمليّات الحسابية باستخدام هذا النّظام ليس سهلًا مثل: عمليّات القسمة والضَرب، والجمع والطرح. - يُعد نظام العد السداسي عشري من أصعب الأنظمة الرقمية في التعامل مع بيانات الحاسوب.

استخدامات نظام العد السداسي عشري
ومن أهم استخدامات نظام العد السداسي عشري ما يأتي:

- تُستخدم أرقام نظام العد السداسي عشري، لتعزيز أمان مواقع الويب، إذ يقوم العديد من المطّورين والمُبرمجين بتحويل الرّقم العشري إلى رقم سداسي عشري، ثم يتم حفظ هذا الرقم في قاعدة البيانات. - يُستخدم نظام العد السداسي عشري في معالجة الحاسوب والأنظمة الإلكترونية الأخرى؛ لزيادة سرعة المعالج. - يُستخدم لتحديد المواقع في الذاكرة، حيث يقوم نظام العد السداسي عشري بتمثيل كل بايت (Byte) على أنه رقمين سداسيّين عشريّين مقارنةً بنظام العد الثنائي.

يُستخدم لتحديد الألوان على صفحات الويب، حيث يتم إعطاء كل لون أساسيّ (أحمر، أخضر، أزرق)، رقمين سداسيّين عشريّين للتّعبير عنه.
يُستخدم لعرض رسائل الخطأ على مواقع الويب، إذ إنّ هذا الاستخدام مفيد جدًا للمُبرمجين في أثناء البحث عن الأخطاء ،وإصلاحها خلال عملية تطوير مواقع الويب .

وفي نهاية البحث عن مفهوم أنظمةِ العد، نجد أنّه على الرّغم من اختلاف أنواعها، فإنها ذاتُ أهميةٍ كُبرى في حياتنا اليوميّة، ويمكننا استنتاج أنّ أيّ نظامِ عدٍ مهما اختلف نوعه، فهو بالتأكيد يُمثل وسيلةً لعرضِ الأعداد وله استخدامات وتطبيقات تخصّه، ويوجد لكل نظامٍ عددٌ محدّدٌ من الرّموز أو العناصر، بالإضافةِ إلى رقم أساسٍ خاصٍ به يُمثله ويُعبر عنه. وقد أدركنا أيضًا أنّ تنوُّع أنظمة العدّ ما هو إلّا أمرٌ نابعٌ من تنوّع وتعدُّد المجالات الحياتيّة المختلفة، فمثلًا يستخدم الإنسان النظام العشري في الحياة اليومية والمعاملات التي تحتاج إلى عمليات رياضية، بينما تستخدم الأجهزة التّكنولوجيّة الرّقميّة من حولنا النّظام الثّنائيّ، وأخيرًا فإنّه لا غنىً عن أنظمة العدّ في حياتنا.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 التحويل من النظام الثنائي إلى النظام العشري

لتحويل أي عدد ثنائي إلى مكافئه العشري فإنه يجب علينا استعمال قانون التمثيل الموضعي للأعداد. و ينطبق هذا القانون عندما يكون الرقم الثنائي صحيحاً أو كسراً مع مراعاة أن أساس نظام العد هنا هو 2 .

مثلاً : إذا كان لدينا العدد 11001 لتحويله إلى العشري نكتب

وإذا كان فيها فاصلة نقوم بالتحويل كالتالي :

مثلاً:

 تحويل الأعداد من النظام العشري إلى الثنائي

لتحويل أي عدد صحيح موجب من النظام العشري إلى الثنائي نستعمل طريقة الباقي Remainder Method الموضحة كالآتي:

1. أقسم العدد العشري على الأساس 2 .
2. أحسب باقي القسمة الذي يكون أما 1 أو 0 .
3. أقسم ناتج القسمة السابق على الأساس 2 كما في خطوة (1).
4. أحسب باقي القسمة كما في خطوة (2).
5. استمر في عملية القسمة وتحديد الباقي حتى يصبح خارج القسمة الصحيح صفراً.
6. العدد الثنائي المطلوب يتكون من أرقام الباقي مقروءة من الباقي الأخير إلى الأول .

مثال: تحويل الرقم 12

         ناتج القسمة        الباقي

          6 = 2÷12             0

          3 = 2÷6              0

          1 = 2÷3              1

          0 = 2÷1              1

فيكون الناتج (من أسفل إلى أعلى ومن اليسار إلى اليمين): 1100

 التحويل من النظام الثماني إلى العشري

للتحويل من النظام الثماني إلى النظام العشري يستعمل قانون التمثيل الموضعي للأعداد مع مراعاة أن أساس نظام العد هنا هو 8 .

أي هو نفس قانون النظام الثنائي ولكن بضربه بـ 8

مثال :

أما في حال وجود فاصلة كما في المثال التالي :

 التحويل من النظام العشري إلى الثماني

تحويل الأعداد الصحيحة الموجبة:لتحويل أي عدد صحيح موجب من النظام العشري إلى الثماني نستعمل طريقة الباقي المشروحة في النظام الثنائي مع مراعاة أن الأساس الجديد هو 8.

مثال تحويل العدد 122 إلى النظام الثماني :

         ناتج القسمة        الباقي

         15 = 8÷122            2

          1 = 8÷15             7

          0 = 8÷1              1

فيكون الناتج (من أسفل إلى أعلى ومن اليسار إلى اليمين): 172

 التحويل من النظام الثماني إلى الثنائي

لتحويل أي عدد ثماني إلى مكافئه الثنائي نستبدل كل رقم من أرقام العدد الثماني بمكافئه الثنائي المكون من ثلاث خانات و بذلك ينتج لدينا العدد الثنائي المكافئ للعدد الثماني المطلوب تحويله.

• 0 -> 000
• 1 -> 001
• 2 -> 010
• 3 -> 011
• 4 -> 100
• 5 -> 101
• 6 -> 110
• 7 -> 111

مثال : تحويل العدد 772

• 7 -> 111
• 7 -> 111
• 2 -> 010

فيكون الناتح : 111111010

في حال وجود فاصلة منقوطة : تحويل العدد 772.5

• 7 -> 111
• 7 -> 111
• 2 -> 010
• 5 -> 101

فالنتاج هو : 111111010.101

 التحويل من النظام الثنائي إلى الثماني

لتحويل الأعداد الثنائية الصحيحة إلى ثمانية نتبع الخطوات التالية:

1. نقسم العدد الثنائي إلى مجموعات كل منها مكون من ثلاث خانات، و يجب أن نبدأ التقسيم من الرقم الأقل أهمية .
2. إذا كانت المجموعة الأخيرة غير مكتملة فإننا نضيف في نهايتها الرقم صفر حتى تصبح مكونة من ثلاث خانات ثنائية.
3. نضم الأرقام الثمانية معاً للحصول على العدد المطلوب.
4. في حالة الكسور الثنائية نبدأ بالتقسيم إلى مجموعات من الخانة القريبة على الفاصلة.

مثال تحويل العدد 1011011010

ففي هذا المثال نبدأ من اليمين :

• 010 -> 2
• 011 -> 3
• 011 -> 3
• 1 نحوله إلى 001 -> 1

فيصبح الرقم 1332

في حال وجود فاصلة

مثال الرقم 1011011010.1011

• 010 -> 2
• 011 -> 3
• 011 -> 3
• 1 نحوله إلى 001 -> 1
• الذي بعد الفاصلة نبدأ فيه من الأول أي
  • 101 -> 5
  • 1 نحوله إلى 100 -> 4

فيكون الناتج : 1332.54

 التحويل من النظام السداسي عشر إلى العشري

للتحويل من النظام السداسي عشر إلى العشري نستعمل قانون التمثيل الموضعي للأعداد مع مراعاة أن أساس هذا النظام هو 16.

مثال تحويل العدد 2AF3

مثال تحويل العدد 0.2A

 التحويل من النظام العشري إلى السداسي عشر

لتحويل الأعداد الصحيحة الموجبة من النظام العشري إلى السداسي عشر: نستعمل طريقة الباقي و ذلك بالقسمة على الأساس16.

مثال تحويل العدد 72

         ناتج القسمة        الباقي

         4 = 16÷72             2

          0 = 16÷4             4

فيكون الناتج هو : 48

 التحويل من النظام السداسي عشر إلى الثنائي

لتحويل أي عدد من النظام السداسي عشر إلى مكافئه الثنائي نتبع الآتي:

1. نستبدل الخانات المكتوبة بدلالة الحروف إن وجدت في العدد بالأعداد العشرية المكافئة لها.
2. نستبدل كل عدد عشري بمكافئه الثنائي المكون من أربعة خانات.
3. ثم نضم الأرقام الثنائية مع بعضها لنحصل على العدد المطلوب .

مثال تحويل العدد D39A

الخطوة الأولى :

• D -> 13
• 3 -> 3
• 9 -> 9
• A -> 10

الخطوة الثانية :

• 13 -> 1101
• 3 -> 0011
• 9 -> 1001
• 10 -> 1010

الخوة الأخيرة :

• يصبح الناتج :

1101001110011010

 التحويل من النظام الثنائي إلى السداسي عشر

لتحويل أي عدد صحيح من النظام الثنائي إلى السداسي عشر نتبع الآتي:

1. نقسم العدد الثنائي إلى مجموعات كل منها يتكون من 4 خانات مع مراعاة أن يبدأ التقسيم من الرقم الأقل أهمية .
2. إذا كانت المجموعة الأخيرة غير مكتملة فإننا نضيف في نهايتها الصفر حتى تصبح مكونة من أربعة خانات .
3. نحول كل مجموعة ثنائية إلى مكافئها في النظام العشري .
4. نستبدل كل رقم عشري(من الخطوة السابقة) أكبر من9 بدلالة حروف النظام السداسي عشر .
5. نضم الأرقام الناتجة مع بعضها لنحصل على الجواب المطلوب في النظام السداسي عشر .

مثال تحويل العدد 101001101101111001101

نجد أنه مؤلف من 1101 1100 1011 1101 0100 0001

• 1101 -> 13
• 1100 -> 12
• 1011 -> 11
• 1101 -> 13
• 0100 -> 4
• 0001 -> 1

بعدها نحوله إلى النظام السداسي عشري

• 13 -> D
• 12 -> C
• 11 -> B
• 13 -> D
• 4 -> 4
• 1 -> 1

فيكون الناتج : 14DBCD

 التحويل من النظام السداسي عشر إلى الثماني

لتحويل أي عدد من النظام السداسي عشر إلى النظام الثماني: نقوم أولاً بتحويله إلى النظام الثنائي كما مر معنا سابقاً و ذلك باستبدال كل رقم من أرقام العدد السداسي عشر إلى مكافئه الثنائي المكون من أربعة خانات، و بعد ضم الأرقام الثنائية إلى بعضها نقوم مرة أخرى بتقسيمها إلى مجموعات من ثلاثة خانات و نستبدل كل مجموعة برقم ثماني و بذلك نكون قد حصلنا على العدد الثماني المطلوب.

مثال : حول العدد السداسي إلى مكافئه الثماني B51.DF2

نقوم بتحويل العدد السداسي عشر إلى مكافئه الثنائي

فنجد أنه يساوي 101101010001,110111110010

ثم نعيد تقسيم العدد الثنائي إلى مجموعات كل منها يتكون من ثلاثة خانات ثنائية ثم نكتب العدد الثماني المكافيء لكل مجموعة

ينتج لنا العدد 5521,6762 هو عدد ثماني

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 التحويل من النظام الثماني إلى السداسي عشر

لتحويل أي عدد ثماني إلى النظام السداسي عشر: نقوم أولاً بتحويله من الثماني إلى الثنائي، ثم نقسم العدد الثنائي الناتج إلى مجموعات كل منها يتكون من أربعة خانات، و نقوم باستبدال كل مجموعة منها بما يكافؤها في النظام السداسي عشر.

مثال: حول العدد الثماني التالي إلى مكافئه السداسي عشري : 163,45

• 1 -> 001
• 6 -> 110
• 3 -> 011
• 4 -> 100
• 5 -> 101
• ثم نضمه إلى أربعة خانات
• نبدأ من قبل الفاصلة أي مع العدد 3 أي 011 ونأخد رقم من آخر خانة للذي قبله فيصبح 0011
• 0011 -> 3

0111 -> 7

• 0 نحوله إلى 0000
  • 0000 -> 0

فيكون الناتج قبل الفاصلة هو 073 الصفر لا داعي له فيكون 73

الرقم الذي بعد الفاصلة نبدأ فيه من الرقم 4 أي من الرقم 100 ونأخذ الرقم الذي بعده فيصبح 1001

• 1001 -> 9
• 01 نحوله إلى 0100
  • 0100 -> 4

فيكون الناتج بعد الفاصلة هو 94

فيصبح الناتج الكلي في النظام السداسي عشري : 73,94