طائرة ورقية (هندسة رياضية)
هذه المقالة عن الشكل الهندسي للطائرة الورقية. إذا كنت تبحث عن الجسم الطائر للطائرة الورقية، انظر طائرة ورقية.
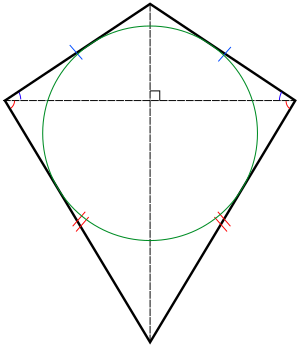
في الهندسة الرياضية، شكل الطائرة الورقية هو شكل رباعي أضلاع فيه كل ضلعين متجاورين متساويين بالطول، على خلاف متوازي الأضلاع الذي يكون فيه كل ضلعين متقابلين متساويين بالطول. سمي شكل الطائرة الورقية على اسم الطائرة الورقية.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
خصائص شكل الطائرة الورقية
- محور تناظر الطائرة الورقية ينطبق على أحد أقطارها.
- قطرا الطائرة الورقية متعامدان.
- يوجد زاويتان متقابلتان متطابقتان.
- تعطى مساحة الطائرة الورقية بالعلاقة: A = d1d2/2.
- تكون الطائرة الورقية رباعي دائري، إذا وفقط إذا كانت مشكلة من مثلثين قائمين. [1]
مراجع
- ^ Gant, P. (1944), "A note on quadrilaterals", Mathematical Gazette 28 (278): 29–30, http://www.jstor.org/view/00255572/ap060279/06a00130/0.
وصلات خارجية
- Eric W. Weisstein, طائرة ورقية at MathWorld.
- Kite definition and area formulae with interactive animations.
 | هذه بذرة مقالة عن الهندسة الرياضية تحتاج للنمو والتحسين، ساهم في إثرائها بالمشاركة في تحريرها. |
الكلمات الدالة: