رفع لأس
الرفع[1] هو عملية رياضية. تكتب صيغته حيث المبنى[2] و القوة[3].
الرفع هو بالأساس عملية ضرب متكرر:
مثلما عملية الضرب هي عملية جمع متكرر:
يستخدم الرفع بشكل واسع في العديد من المجالات منها الاقتصاد وعلم الأحياء والكيمياء والفيزياء وعلوم الحاسوب (المعلوماتية) مع تطبيقات مثل النمو السكاني وسير تفاعل كيميائي وخواص الموجات وعلم التشفير.
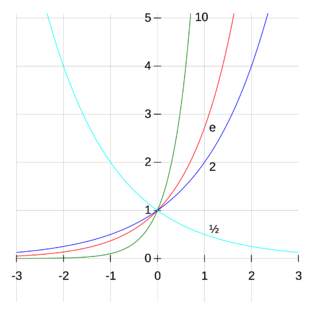
الأس المعقد للأرقام الحقيقية الموجبة
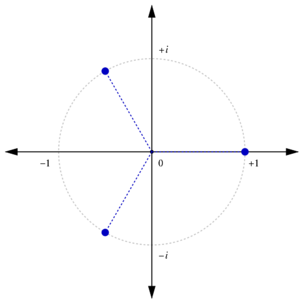
الأس التخيلي لـ e

الدالة الأسية ez يمكن تعريفها بأنها نهاية (1 + z/N)N, باقتراب N من مالانهاية، وبذلك فإن eiπ هي نهاية (1 + iπ/N)N. وفي هذا التحريك، فإن N تأخذ قيم مختلفة متزايدة من 1 إلى 100. حساب (1 + iπ/N)N يُعرض كتأثير مجمَّع لعمليات ضرب مكررة N مرة في complex plane، وتكون النقطة النهائية هي القيمة الفعلية لـ (1 + iπ/N)N. يمكن رؤية أنه كلما أصبحت N أكبر، فإن (1 + iπ/N)N تقترب من النهاية −1. ولذلك، eiπ = −1, تُعرف بإسم هوية اويلر.
أسس الأرقام المركبة
الجذور المركبة للوحدة
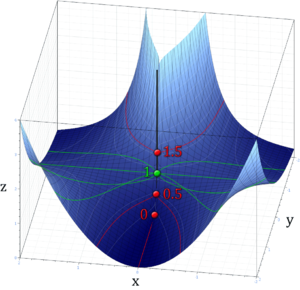
صفر مرفوع إلى الأس الصفري
انظر أيضا
|
|
مراجع
- ^ أو الترقية
- ^ أو الأساس أو القاعدة
- ^ أو الأس أو الداعية[بحاجة لمصدر]