دوران (رياضيات)
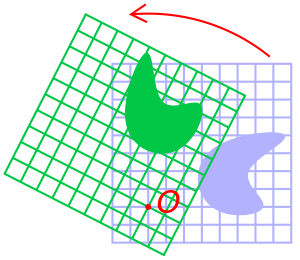
الدوران Rotation، في الرياضيات، هو مفهوم منشؤه في علم الهندسة. أي دروان هو عبارة عن حركة لفضاء معين يحافظ على على الأبعاد، في المستوى أو الفراغ. بالإضافة إلى الإزاحة والانعكاس. ونعني بالدوران بكلمات بسيطة، دوران شكل باتجاه معين (مع أو ضد عقارب الساعة)، حول نقطة معينة (هي مركز الدوران)، بزاوية معينة (هي مقدار هذا الدوران). فعندما تدور الأرض حول الشمس مثلا، يكون اتجاه الدوران من الغرب إلى الشرق، ومركز الدوران هو الشمس. وقد يكون الدوران بزاوية معينة، وعندما يكون بزاوية 90 درجة نسميه ربع دورة. وعندما يكون بزاوية 360 درجة نسميه دورة كاملة. وقد يكون أكثر من ذلك، كما في دوران الأرض حول الشمس، مثلا.[1]
يحافظ الدوران على شكل الجسم الذي نقوم بتدويره وعلى حجمه. والشكل الناتج من الدوران مطابق تماماً للشكل قبل الدوران. إذا دورنا مثلثاً مثلاً، فان الناتج سيكون مثلثاً مطابقاً.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
التعريف
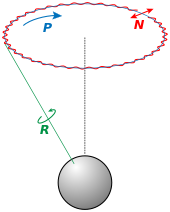
الدوران هو تحويل هندسي، كثيراً ما نشاهده ونلمسه في حياتنا اليومية، مثل حركة المروحة الهوائية التي ثُبّتت في سقف الغرفة.
تحويل الدوران يُدير كل المستوي حول نقطة معينة وبزاوية معينة، كل نقاط المستوي تدور حول نفس النقطة وبنفس الزاوية، لذا عند وصف الدوران لا بد من ذكر زاويته ومركزه.
يمكن تمييز التحويل الدوراني بأمرين:
1- نقطة دوران.
2- زاوية دوران.
مركز الدوران
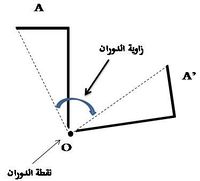
يلعب مركز الدوران دورا مشابها للدور الذي يلعبه خط التماثل في الانعكاس، فكما أن لكل انعكاس خط انعكاس كذلك فإن لكل دوران هناك مركز دوران، ويمكن القول أن الدوران يتحدد بثلاثة أمور هي: زاوية الدوران، اتجاه الدوران، ومركز الدوران.
لو أدرنا مسطرة حول نقطة في وسطها، لاختلف الشكل الذي نحصل عليه للمسطرة مما لو أدرناها حول نقطة في طرفها، حتى لو كانت زاوية الدوران واحدة في الحالتين، واتجاه الدوران واحدا.
ويشترك مركز الدوران مع خط الانعكاس في صفة أخرى: فمركز الدوران الذي هو نقطة لا يدور، تماما كما أن النقاط على خط الانعكاس لا تتحرك من مكانها بفعل الانعكاس.
تعريفات وتمثيلات
في الهندسة الإقليدية
مقالات مفصلة: فضاء إقليدي #الدورانات والانعكاسات- المجموعة المتعامدة الخاصة
الشكل الجبري الخطي ومتعدد الخطوط
ثنائي الأبعاد
- مقالة مفصلة: عدد مركب
ثلاثي الأبعاد
الكواتيرنيون
في الهندسة غير الإقليدية
في النسبية
دورانات منفصلة
الأهمية
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
تعميمات
انظر أيضاً
- محاور الطائرة الرئيسسية
- Charts on SO(3)
- احداثيات الدوران والانعكاسات
- دوران متناهي الصغر
- Irrational rotation
- Orientation (geometry)
- Rodrigues' rotation formula
- Vortex
مرئيات
<embed width="320" height="240" quality="high" bgcolor="#000000" name="main" id="main" >http://media.marefa.org/modules/vPlayer/vPlayer.swf?f=http://media.marefa.org/modules/vPlayer/vPlayercfg.php?fid=2e2a7984afa4480a6d6" allowscriptaccess="always" allowfullscreen="false" type="application/x-shockwave-flash"/</embed>
|
| الدوران. |
الهوامش
المصادر
- Hestenes, David (1999). New Foundations for Classical Mechanics. Dordrecht: Kluwer Academic Publishers. ISBN 0-7923-5514-8.
- Lounesto, Pertti (2001). Clifford algebras and spinors. Cambridge: Cambridge University Press. ISBN 978-0-521-00551-7.
- Brannon, Rebecca M. (2002). "A review of useful theorems involving proper orthogonal matrices referenced to three-dimensional physical space" (PDF). Albuquerque: Sandia National Laboratories.