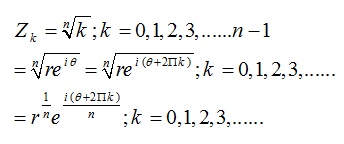درس:مقدمة في الأعداد العقدية

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 مجموعة الأعداد العقدية

تعرف مجموعة الأعداد العقدية التي نرمز لها بالرمز (C|) بأنها جميع الكميات من الشكل a+ib فإذا كان Z ∈ |C يمكن كتابته بالشكل Z=a+ib

نسمي a بالقسم الحقيقي للعدد العقدي ونرمز له بالرمز Re(Z)=a

نسمي b بالقسم التخيلي للعدد العقدي ونرمز له بالرمز Im(Z)=b

كما نسمي i بالوحدة التخيلية وتساوي (-1)√ (جذر الـ -1) أي (i = √(-1

 تساوي عددين عقديين

إذا كان $Z_{1}=a_{1}+ib_{1}$ و $Z_{2}=a_{2}+ib_{2}$ ينتميان إلى (C|)

نقول أن $Z_{1}=Z_{2}$ إذا كان $a_{1}=a_{2}$ و $b_{1}=b_{2}$

 العمليات على الأعداد العقدية

 جمع (طرح) عددين عقدين

إذا كان $Z_{1}=a_{1}+ib_{1}$ و $Z_{2}=a_{2}+i_{b}2$ ينتميان إلى (C|)

فعندئذ يعرف جمع (طرح) هذين العددين بالشكل التالي :

($Z_{1}$∓$Z_{2}$ = $a_{1}$∓$a_{2}$ + i ($b_{1}$∓$b_{2}$

 ضرب عددين عقديين

إذا كان $Z_{1}=a_{1}+ib_{1}$ و $Z_{2}=a_{2}+ib_{2}$ ينتميان إلى (C|)

عندئذ نعرف جداءهما بالشكل :

($Z_{1}$×$Z_{2}$ =$a_{1}$ $a_{2}$−$b_{1}$ $b_{2}$ +i($a_{1}$ $b_{2}$+$a_{2}$ $b_{1}$

 قسمة عددين عقديين

إذا كان $Z_{1}=a_{1}+ib_{1}$ و $Z_{2}=a_{2}+ib_{2}$ ينتميان إلى (C|)

عندئذ نعرف قسمة Z = $Z_{1}/Z_{2}$

فبفرض Z = α + iβ

لدينا$Z_{1}=ZZ_{2}$

نعوض فنجد

($a_{1}+ib_{1}$ = (α + iβ)($a_{2}+ib_{2}$

($a_{1}$+i$b_{1}$ = (α $a_{2}$ - β $b_{2}$)+i(α $b_{2}$ + β $a_{2}$

بالمطابقة نجد

$a_{1}$ = α $a_{2}$ - β $b_{2}$

$b_{1}$ = α $b_{2}$ + β $a_{2}$

بحل جملة المعادلتين السابقتين بحسب أي طريقة (حسب كرمر مثلاً) تنتج α و β التين تمثلان مركبات العدد العقدي Z = $Z_{1}$/$Z_{2}$

الحل :

$\triangle ={\begin{vmatrix}a_{2}&b_{2}\\b_{2}&a_{2}\end{vmatrix}}={a^{2}}_{2}-{b^{2}}_{2}$

$\triangle _{\beta }={\begin{vmatrix}a_{1}&b_{2}\\b_{1}&a_{2}\end{vmatrix}}=a_{1}.a_{2}-b_{1}.b_{2}$

$\triangle _{\alpha }={\begin{vmatrix}a_{2}&a_{1}\\b_{2}&b_{1}\end{vmatrix}}=a_{2}.b_{1}-a_{1}.b_{2}$

ويكون :

$\alpha ={\frac {\triangle _{\alpha }}{\triangle }}$

$\beta ={\frac {\triangle _{\beta }}{\triangle }}$

 طويلة العدد العقدي

إذا كان $Z=a+ib$ ينتمي إلى (C|) فعندئذ تعرف طويلة ها العدد بالشكل |Z| وتساوي (Z|=√(a^2+b^2| وهي دوماً أكبر أو تساوي الصفر

 مرافق عدد عقدي

إذا كان $Z=a+ib$ ينتمي إلى (C|) فعندئذ يعرف مرافقه بالشكل التالي إذا كان $Z=a-ib$

 نظريات

 نظرية 1

1. طويلة العدد العقدي يساوي إلى طويلة مرافقه
2. مربع طويلة عدد عقدي يساوي إلى العدد العقدي بمرافقه
3. القيمة المطلقة للقسم الحقيقي للعدد العقدي أصغر أو تساوي العدد العقدي
4. القيمة المطلقة للقسم التخيلي للعدد العقدي أصغر أو تساوي العدد العقدي
5. $|Z_{1}+Z_{2}|$ أصغر أو تساوي $|Z_{1}|+|Z_{2}|$
6. $|Z_{1}Z_{2}|$ أصغر أو تساوي $|Z_{1}||Z_{2}|$
7. $|Z_{1}/Z_{2}|=|Z_{1}|/|Z_{2}|$
8. $|Z_{1}|-|Z_{2}|=|Z_{1}-Z_{2}|$

 نظرية 2

1. مرافق مجموع عددين عقديين يساوي إلى مرافق الأول مجموعاً إليه مرافق الثاني
2. مرافق ضرب عددين عقديين يساوي إلى مرافق الأول مضرب بمرافق الثاني
3. مرافق قسمة عددين عقديين يساوي إلى مرافق الأول مقسوماً عليه مرافق الثاني بحيث الثاني لا يساوي الصفر

 تعريف المتحول العقدي

إذا كان $x,y$ متحولين عندئذ يسمى $Z=x+iy$ بالمتحول العقدي

 نظرية

إن معادلة الدائرة التي مركزها $Z_{0}$ ونصف قطرها r تعطى بالعلاقة $Z-Z_{0}|=r|$

 تعريف القرص الدائري المغلق

هو مجموعة من النقاط Z تحقق المتراجحة $|Z-Z_{0}|$ أصغر أو تساوي r قرص دائري مغلق مركزه $Z_{0}$

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 تعريف القرص الدائري المفتوح

هو مجموعة من النقاط Z تحقق المتراجحة $|Z-Z_{0}|$ أصغر تماماً من r قرص دائري مفتوح مركزه $Z_{0}$

إذا كان r تساوي إبسلون (حيث إبسلون صغير بما فيه الكفاية) نسمي النقاط Z التي تحقق المتراجحة $|Z-Z_{0}|$ أصغر تماماً من إبسلون بجوار النقطة $Z_{0}$

 تعريف الحلقة الدائرية المغلقة

إذا كان $C_{1}$ و $C_{2}$ دائرتان متحدتان بالمركز $Z_{0}$ نصف قطريهما على الترتيب $r_{1}$ و $r_{2}$ بحيث أن $r_{1}$ أصغر من $r_{2}$ عندئذ تسمى مجموعة النقاط Z التي تحقق المتراجحة $r_{1}\leq |Z-Z_{0}|\leq r_{2}$ بحلقة دائرية مغلقة مركزها$Z_{0}$ ,وبشكل مشابه تعرف الحلقة الدائرية المفتوحة .

 الشكل المثلثي أو القطبي للعدد العقدي

إذا كان $Z=x+iy$ عدداً عقدياً فعندئذٍ يعرف الشكل المثلثي لهذا العدد بالشكل : $z=r(cos\theta +isin\theta )$ < حيث (r=√(x^2+y^2 و θ هي زاوية العدد العقدي أو مضمونه أو سعته

(θ=Arg(Z و ِArg هو الوسيط

يتم الصول على الزاوية θ كما يلي :

1. إذا كان x أكبر من صفر (θ=arc tan (y/x
2. إذا كان x أصغر من الصفر وy أكبر أو تساوي الصفر θ=arc tan(y/x)+π
3. إذا كان x أصغر من الصفر وy أصغر من الصفر θ=arc tan(y/x)-π
4. إذا كان x تساوي الصفر وy أكبر من الصفر θ=π/2
5. إذا كان x تساوي الصفر وy تساوي الصفر θ=-π/2

 الشكل الأسي للعد العقدي

إذا كان $Z=x+iy$ عدداً عقدياً عندئذ يعرف العدد لاأسي لهذا العدد بالشكل التالي (Z=r e^(iθ

حيث (r=√(x^2+y^2 و tan θ = y/x

ملاحظة :

إذا كان (Z=r e^(iθ عندئذ فإن مرافقه يساوي (Z=r e^(-iθ

$((Z_{1}Z_{2}=r_{1}r_{2}$ e^(i(θ_1+θ_2

$((Z_{1}/Z_{2}=r_{1}/r_{2}$ e^(i(θ_1-θ_2

 نظرية

1. e^(iθ)=cosθ+i sinθ
2. ((e^(iθ)=e^(i(θ+2πk بحيث k = ∓1 ,∓2 ,∓3,....etc

 قوى وجذور العدد العقدي

إذا كان n عدداً طبيعياً وكان Z عدداً عقدياً فإننا نرمز لجداء Z بنفسه n مرة Z^n

فإن كان (Z=r e^(iθ فإن (Z^n=r^n e^(inθ

إذا كان r=1 فعندئذ (e^(iθ)n=e^(inθ

e^(iθ)n=(cosθ+i sinθ)^n

(e^(iθ)n=(cos nθ+i sin nθ

وتسمى العلاقة الأخيرة بعلاقة ديم وافر

إذا كان Z عدداً عقدياً وطلب منا ايجاد الجذر النوني لهذا العدد فإننا نتبع الخطوات التالية :

من العلاقة الأخيرة يعطى الجذرالنوني للعدد العقدي