درس:الموجة الجيبية

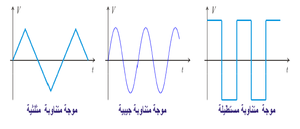
الموجة المتناوبة: هي عبارة عن فلطية أو تيار متغيرة بشكل متكرر بتغير الزمن، بحيث تكون قيمتها موجبة تارة، وسالبة تارة أخرى. لها أنواع مختلفة، مثل الموجات المستطيلة، الموجات الجيبية، والموجات المثلثية.

يستخدم الرمز AC للدلالة على التيار المتناوب Alternate Current بينما يستخدم الرمز DC للدلالة على التيار المستمر Direct Current.

ما الذي يمتاز به التيار المتناوب عن التيار المستمر؟ في الحقيقة قد لا توجد له ميزات في التطبيقات التي تستخدم فيها الكهرباء لتبديد الطاقة على شكل حرارة. لكن هذا الأمر يختلف عند التحدث عن التطبيقات الأعقد. فمن أجل نقل الطاقة على مسافات بعيدة، يمكننا التحكم بمطال التيار، فنرفع مطال الفلطية إلى قيمة عالية بحيث تصبح قيمة مطال التيار منخفضة، وهذا ما يخفف بشكل كبير من الاستطاعة التي تستهلكها مقاومة الأسلاك، إذا ما قارناها بالاستطاعة المستهلكة عندما يكون التيار مستمرا.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الموجة الجيبية

الموجة الجيبية هي فلطية أو تيار تتغير بشكل جيبي مع الزمن ، يمكن تمثيل أية موجة بعلاقة من الشكل:

$a(t)=A\sin(\omega t+\theta )\,\,$

بما أن القيمة العظمى التي يصلها التابع الجيبي هي الواحد، فسيكون المعامل المضروب به A هو القيمة العظمى التي تأخذها الموجة، أي مطال أو سعة الموجة، ويكون مقدرا بالفولط أو بالآمبير.

المقدار$(\omega t+\theta )\,\,$ هو صفحة الموجة، ويقدّر بالراديان.

أما بالنسبة لـ $\omega \,\,$ فهو نبض الموجة. ويقدر بالراديان/ثا. والمقدار خطأ رياضيات (خطأ في الصيغة): {\displaystyle θ\,\,} يسمى الطور (الصفحة الابتدائية للموجة) ويقدر بالراديان. سنتناول الآن بالشرح هذه المفاهيم.

 نبض الموجة

حتى نستطيع استيعاب المدلول الفيزيائي لهذا المفهوم علينا أن ننتظر حتى نتعرف على طريقة تمثيل الموجة الجيبية. وسنكتفي الآن أن نشير إلى هذا المقدار يرتبط بكل من دور وتواتر الموجة الجيبية وفق العلاقة:

$\omega =2\pi f={\frac {2\pi }{T}}\,\,$

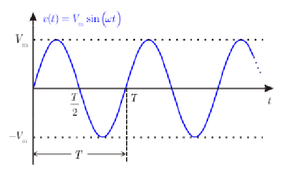
دور الموجة T هو المدة الزمنية التي تفصل بين مرورين متعاقبين للموجة من الصفر (أو أية قيمة أخرى)، ويقدر بالثانية.

تواتر (تردد) الموجة f هو مقلوب الدور، ويقدر بالهرتز، ويعبر عن عدد المرات التي تتكرر فيها الموجة في الثانية واحدة.

الموجة الجيبية التي تستخدم في التغذية الكهربائية للمدينة ذات تردد 50Hz ومطال 220V.

 الطور

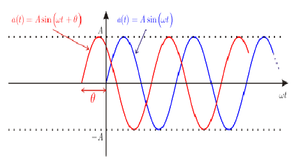
في اللحظة الزمنية t = 0 تكون صفحة التابع الجيبي: $\omega t+\theta =0+\theta =\theta \,$ . فالطور يعبر عن الصفحة الابتدائية للموجة الجيبية.

لنحاول أن نفهم الطور بطريقة مختلفة. لتكن لدينا موجة جيبية أخرى هي$a_{0}(t)=A\sin(\omega t)\,$. يعبر الطور هنا عن فرق الصفحة بين الموجة المدروسة $a\,$ والموجة الأخرى$a_{0}\,$ والتي غالبا ما تسمى بالموجة المرجعية. لهذافالطور مقدار نسبي وليس مقدارا مطلقا خاصا بالموجة، وفي حال كانت موجبة، نقول أن$a\,$ متقدمة بالطور$a_{0}\,$ على (كما هو الحال في الشكل)، وفي حال كانت خطأ رياضيات (خطأ في الصيغة): {\displaystyle θ\,} سالبة، نقول أن $a\,$ متأخرة بالطور عن $a_{0}\,$.

 تمثيل الموجة الجيبية

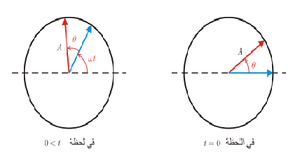
يمكن تمثيل الموجة الجيبية بشعاع طويلته هو مطال الموجة A، يدور بعكس اتجاه عقارب الساعة بسرعة زاوية هي نبض الموجة. في الشكل أدناه قمنا بتمثيل الموجتين السابقتين: و.

يمثل الشكل الأول وضع الموجتين الجيبيتين في اللحظة $t=0\,$. عندها تكون صفحة التابع $A_{0}\,$ مساوية للصفر، لذلك فإنه يكون منطبقا على المحور الأفقي. أما بالنسبة للتابع $a\,$ فإن صفحته ستكون وهي نفسها الزاوية التي يصنعها الشعاع مع المحور الأفقي. وبما أن الشعاعان يدوران بنفس السرعة الزاوية ، فإنهما بعد فترة زمنية ما $t\,$ سيأخذان الوضع المبين في الشكل الثاني، حيث نجد أن الزاوية التي يصنعها كل من الشعاعان السابقان ازدادت بالمقدار نفسه$\omega t\,$ فيما حافظ كل من الشعاعين على الوضع النسبي بينهما (لاحظ أن الفرق الزاوي بينهما بقي ). ولهذا السبب فإن تمثيل الموجات الجيبية في اللحظة الزمنية$t=0\,$. يكون كافيا تماما من أجل توصيف الدارة.

من الشكل أيضا يتبين لنا وضوح معنى تقدم أو تأخر موجة جيبية على أخرى، فعندما تكون موجة ما متقدمة على موجة أخرى، فإن الشعاع الممثل للموجة الأولى "سيسبق" الشعاع الممثل للثانية.

 المطاور

بما أن دور التيارات المتناوبة غالبا ما تكون قصيرة جدا (1/50 ثا مثلا) فإننا غالبا ما لا نكترث بالتمثيل الزمني الآني للموجة المتناوبة، بل نقصر اهتمامنا على مطال (سعة) الموجة A وطورها ، ولهذا يمكن أن نصف موجة ما باستخدام هذين المقدارين الذين يكتبان ككتلة واحدة تسمى المطاور بالشكل التالي: $A{\angle }\theta \,$ .

مثال: لتكن لدينا الموجة التالية:$a(t)=1.273\sin(\omega t+30^{o})\,$، فيكون المطاور في هذه الحالة$1.273{\angle }30^{o}\,$ وبما أنه من الشائع استخدام القيمة المنتجة (وهي السعة مقسومة على${\sqrt {2}}\,$ وسنشرحها بعد قليل إن شاء الله)، فإن المطاور يصبح بالشكل: $0.9{\angle }30^{o}\,$.

 القيمة الوسطى لمقدار جيبي

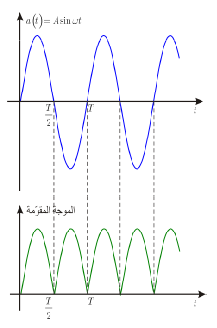
لتكن لدينا الموجة الجيبية التالية: $a(t)=A\sin(\omega t)\,$.

نلاحظ أن القيمة المتوسطة لهذه الموجة على دور واحد $T\,$ ستكون صفرا. لأن الموجة في نصف الدور الثاني ستكرر نفسها ولكن بقيم سالبة. (حاول أن تتأكد من ذلك بنفسك!).

لهذا السبب، نعرف القيمة الوسطية $A_{a}v\,$ للمقدار الجيبي $a\,$ على أنها القيمة الوسطية للموجة المقومة على دور كامل. وبالتالي نجد أنها:

$A_{\mathit {av}}={\frac {2}{T}}\int _{0}^{t}{A\sin(\omega t)}{\mathit {dt}}={\frac {2A}{\pi }}\,$

 القيمة المنتجة لموجة جيبية

تعرف القيمة المنتجة (أو قيمة الجذر المتوسط التربيعي rms) لتيار متناوب على أنها قيمة التيار المستمر الذي لو مر في المقاومة لقدم إليها ذات الاستطاعة التي يقدمها التيار المتناوب. أو لنقل بشكل أبسط أنها قيمة التيار المستمر الذي لو مر في المقاومة نفسها لقام بتوليد كمية حرارة مماثلة خلال الزمن ذاته.

نعلم أن الاستطاعة التي تستهلكها مقاومة $R\,$ إذا مر فيها تيار متناوب $i\,$ هي: $p={\mathit {Ri}}^{2}\,$

وبالتالي تكون الاستطاعة الوسطية المستهلكة خلال دور واحد:

$P={\frac {1}{T}}\int _{0}^{T}{{\mathit {Ri}}^{2}}{\mathit {dt}}={\frac {R}{T}}\int _{0}^{T}{i^{2}}{\mathit {dt}}\,$

أما الاستطاعة التي يقدمها تيار مستمر $I_{e}ff\,$ لهذه المقاومة: $P={\mathit {RI}}_{\mathit {eff}}^{2}\,$

وبالتالي نجد أن قيمة التيار المنتجة: $I_{\mathit {eff}}={\sqrt {{\frac {1}{T}}\int _{0}^{T}{i(t)}^{2}{\mathit {dt}}}}\,$

وبالطريقة ذاتها نجد أن القيمة المنتجة للفلطية هي: $V_{\mathit {eff}}={\sqrt {{\frac {1}{T}}\int _{0}^{T}{v(t)}^{2}{\mathit {dt}}}}.\,$

ومن أجل $i(t)=I_{m}\sin(\omega t)\,$ نجد أن: $I_{\mathit {eff}}={\frac {I_{m}}{\sqrt {2}}}\,$ وبطريقة مماثلة نجد أن $V_{\mathit {eff}}={\frac {V_{m}}{\sqrt {2}}}\,$

ملاحظة: سنحصل على النتائج نفسها من أجل: $i(t)=I_{m}\sin(\omega t+\theta )\,$

 تمثيل مقدار جيبي بقيمة عقدية

لو اضطررت للتعبير عن المسافة بين مدينتين، لكان بإمكاني أن أقدّم جوابا مؤلفا من رقم واحد، مرفقا بواحدة الميل أو الكيلومتر أو أية واحدة طول أخرى. أما لو اضطررت أن أعبر تعليمات السفر من مدينة لأخرى فلن يكفي عندها ما ذكرته آنفا: ففضلا عن مسافة السفر، يجب أن أذكر شيئا عن الاتجاه.

يسمى نوع المعلومات الذي يعبّر عن مقدار أحادي البعد (المسافة الخطية في مثالنا) بالمقدار السلمي. والأعداد السلمية هي ذلك النوع من الأعداد الذي استخدمناه في معظم التطبيقات الرياضية التي تعلمناها حتى الآن. فالفلطية التي تولّدها البطارية في دارة تيار مستمر مقدار سلمي، ومثلها مقاومة سلك نحاسي (أوم)، والتيار المار به (آمبير).

لكننا نجد أننا وعند تحليل دارات التيار المتناوب، فإن مقادير الفلطية والتيار والممانعة كلها لم تعد مقاديرا أحادية البعد كما اعتدناها أن تكون في دارات التيار المستمر، فبما أنها مقادير "ديناميكية" (أي متناوبة الجهة والطويلة) فإنها تمتلك أبعادا أخرى يجب مراعاتها: والتواتر والطور هما من المقادير التي يجب مراعاتها،

لهذه الأسباب سنتعامل مع تقانات وكائنات رياضية تستطيع تمثيل هذه المقادير متعددة الأبعاد، وسنستخدم لهذا الأمر الأعداد العقدية بدلا عن الأعداد السلمية الحقيقية. تماما كما في إعطاء تعليمات السفر بين مدينتين، فكما مر معنا لكل مقدار في التيار المتناوب سعة (تشابه المسافة)، وطور (تشابه الجهة)، والعدد العقدي يستطيع التعبير هذين البعدين، أي السعة والطور، في الوقت ذاته. سنقوم الآن ببعض العمليات الرياضية وبالاعتماد على علاقة أويلر للتوصل إلى التمثيل العقدي للتيار المتناوب.

ليكن لدينا التيار التالي: $i(t)=I_{m}\sin(\omega t+\theta )\,$

نعلم أن أي عدد عقدي يكتب بالشكل التالي: $z=[r,\theta ]=r(\cos \theta +j\sin \theta )\,$

وحسب علاقة أويلر يمكننا أيضا أن نكتب: $e^{j\theta }=\cos \theta +j\sin \theta \,$

وبالتالي فمعادلة التيار المعطاة بدلالة التابع تمثل الجزء التخيلي من عدد عقدي. يمكننا أن نعبر عن كلامنا هذا بالتالي:

$I_{m}\sin(\omega t+\theta )={\mathit {Ima}}(I_{m}(\cos(\omega t+\theta )+j\sin(\omega t+\theta )))={\mathit {Ima}}(I_{m}e^{j(\omega t+\theta )})\,$

سنستخدم العدد العقدي $I_{m}e^{j\theta }\,$ للتعبير عن التيار. لاحظ أن صيغة التمثيل هذه هي ذاتها صيغة تمثيل المطاور. فعند تمثيل هذا العدد العقدي بيانيا في المستوي العقدي، سنحصل على العدد العقدي الممثل بالشعاع ذي الطويلة$I_{m}\,$ وذي الزاوية $\theta \,$ .

نلاحظ أننا أسقطنا الزمن في التمثيل العقدي للتيار المتناوب، وهذا صحيح. فالتمثيل $i(t)\,$ هو التمثيل الزمني، أما التمثيل العقدي $I\,$ المطاور فهو التمثيل في الحقل الترددي (رغم عدم ظهور التردد فيه).

ومن خلال الطريقة ذاتها، نجد أنه بإمكاننا تمثيل الفلطية $i(t)=I_{m}\sin(\omega t+\theta )\,$ بالعدد العقدي $V_{m}e^{j{\phi }}\,$.