درس:الاستطاعة

نعلم أن الاستطاعة الآنية لعنصر تعطى بالعلاقة: ${\displaystyle{\displaystyle p(t)=v(t)i(t)\,}}$، وفي حال عنصر يخضع لتيار متناوب، تأخذ علاقة كل من الفلطية والتيار الشكلين التاليين:

${\displaystyle{\displaystyle v(t)=V_{m}\sin(\omega t+{\theta}_{1})\,}}$

${\displaystyle{\displaystyle i(t)=I_{m}\sin(\omega t+\theta_{2})\,}}$

وبالتالي يمكننا أن نحسب الاستطاعة الآنية لهذا العنصر، فتكون (وباستخدام بعض التحويلات المثلثية!):

${\displaystyle{\displaystyle p(t)=I_{m}V_{m}\sin(\omega t+\theta_{1})\sin(\omega t+\theta_{2})={\frac{-1}{2}}I_{m}V_{m}[\cos(2\omega t+\theta_{1}+\theta_{2})-\cos(\theta_{1}-\theta_{2})]\,}}$

أي${\displaystyle{\displaystyle p(t)={\frac{1}{2}}I_{m}V_{m}[\cos(\theta_{1}-\theta_{2})-\cos(2\omega t+\theta_{1}+\theta_{2})]\,}}$

الآن يمكننا حساب الاستطاعة الوسطية المستهلكة خلال دور واحد من خلال العلاقة التالية: ${\displaystyle{\displaystyle P={\frac{1}{T-0}}\int_{0}^{T}{p(t)\{dt}\,}}$

وبالتالي:خطأ رياضيات (خطأ في الصيغة): {\displaystyle P=\frac{1}{T}V_{m}I_{m}[\int _{0}^{T}\cos (\theta _{1}-\theta_{2})\{dt}-\int _{0}^{T}{\cos (2\omega t+\theta _{1}+\theta_{2})\{dt}}] \,} التكامل الأول هو تكامل لمقدار ثابت لا يتعلق بالزمن. أما الثاني فهو تكامل لتابع جيبي نبضه ${\displaystyle{\displaystyle 2\omega\,}}$ فهو معدوم، ومنه:

${\displaystyle{\displaystyle P={\frac{1}{2T}}V_{m}I_{m}[T\times\cos(\theta_{1}-\theta_{2})-0]={\frac{1}{2}}V_{m}I_{m}\cos(\theta_{1}-\theta_{2})={\frac{1}{\sqrt{2}}}{\frac{1}{\sqrt{2}}}V_{m}I_{m}\cos(\theta_{1}-\theta_{2})\,}}$

ومنه:${\displaystyle{\displaystyle{P=V_{\mathit{eff}}I_{\mathit{eff}}\cos(\theta_{1}-\theta_{2})=V_{\mathit{eff}}I_{\mathit{eff}}\cos\phi}\,}}$

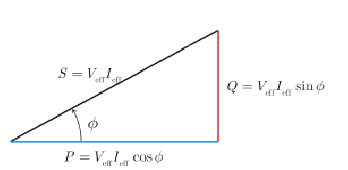
يسمى المقدار${\displaystyle{\displaystyle\phi=\theta_{1}-\theta_{2}\,}}$ بعامل استطاعة الدارة. ويسمى المقدار ${\displaystyle{\displaystyle S=V_{\mathit{eff}}I_{\mathit{eff}}\,}}$ بالاستطاعة الظاهرية وتقاس بواحدة الفولط آمبير VA.

أما المقدار${\displaystyle{\displaystyle Q=V_{\mathit{eff}}I_{\mathit{eff}}\sin\phi\,}}$ فهو الاستطاعة التفاعلية، وتقاس بواحدة الفولط آمبير التفاعلية VAR (اختصارا لـ Volt-Ampère-Reactive). ويمكن تمثيل المقادير الثلاث السابقة في مثلث الاستطاعة القائم.

ونلاحظ أن ${\displaystyle{\displaystyle S={\sqrt{P^{2}+Q^{2}}}\,}}$

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

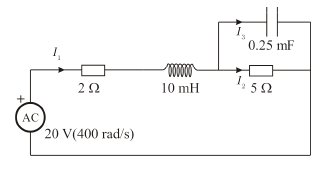
 مثال محلول

لتكن لدينا الدارة المبينة بالشكل، وبفرض أن النبض ${\displaystyle{\displaystyle\omega=400{\mathit{rad}}/s\,}}$ والقيمة المنتجة للمنبع هي 20V:

1. احسب التيار العقدي ${\displaystyle{\displaystyle I_{1}\,}}$ ثم التيارين العقديين ${\displaystyle{\displaystyle I_{2}\,}}$ و${\displaystyle{\displaystyle I_{3}\,}}$.
2. احسب الاستطاعة المستهلكة في المقاومة ${\displaystyle{\displaystyle 2\omega\,}}$، وفي المقاومة ${\displaystyle{\displaystyle 5\omega\,}}$.
3. احسب الاستطاعة التفاعلية الكلية في الدارة ${\displaystyle{\displaystyle Q\,}}$.
4. احسب عامل الاستطاعة لهذه الدارة، ثم الاستطاعة الكلية المستهلكة فيها.

الحل:

الطلب الأول:. نعلم أن التيار العقدي ${\displaystyle{\displaystyle I_{1}\,}}$ يعطى بالعلاقة:${\displaystyle{\displaystyle I_{1}={\frac{V}{Z_{E}}}\,}}$ لذلك فإننا سنقوم بحساب الممانعة الكلية للدارة.

لنقم أولا بحساب الممانعة المكافئة لكل من المكثفة والمقاومة ${\displaystyle{\displaystyle 5\omega\,}}$.

${\displaystyle{\displaystyle Z_{C}=-jX_{C}=-j{\frac{1}{\omega C}}=-j{\frac{1}{400\times 0.2510^{-3}}}=-j10\Omega\,}}$

و${\displaystyle{\displaystyle Z_{5\Omega}=5\Omega\,}}$

فالممانعة المكافئة هي: ${\displaystyle{\displaystyle Z_{1}={\frac{Z_{5\Omega}Z_{C}}{Z_{5\Omega}+Z_{c}}}={\frac{-50j}{5-10j}}\,}}$

عندما نضطر إلى تقسيم (أو ضرب) عددين عقديين فإننا غالبا لا نلجأ إلى ضرب البسط والمقام بمرافق المقام، بل نقوم بتحويل العددين إلى الشكل المطاور الأسهل نسبيا حيث سنقوم بتقسيم الطويلتين، وطرح الزاويتين فقط.

من أجل تحويل عدد عقدي ${\displaystyle{\displaystyle x+jy\,}}$ إلى الشكل المطاور${\displaystyle{\displaystyle A{\angle}\theta\,}}$ نستخدم العلاقات التالية:

للتحويل إلى شكل المطاور:${\displaystyle{\displaystyle A={\sqrt{x^{2}+y^{2}}}\,}}$ و ${\displaystyle{\displaystyle\theta=\arctan({\frac{y}{x}})\,}}$

للعودة إلى الشكل العقدي التقليدي: ${\displaystyle{\displaystyle x=A\cos\theta\,}}$ و${\displaystyle{\displaystyle y=A\sin\theta\,}}$

إذاً يمكننا الآن أن نقوم بإعادة كتابة ${\displaystyle{\displaystyle Z_{1}\,}}$ بالشكل:

${\displaystyle{\displaystyle Z_{1}={\frac{50{\angle}-90^{o}}{11.18{\angle}-63.43^{o}}}=4.473{\angle}-26.57^{o}=4-2j\,}}$

الآن نحسب ممانعة الوشيعة فنجدها: ${\displaystyle{\displaystyle Z_{L}=jX_{L}=j\omega L=(400\times 10\times 10^{-3})=4j\,}}$

وبالتالي يمكننا الآن حساب الممانعة الكلية: ${\displaystyle{\displaystyle Z_{E}=Z_{2\Omega}+Z_{L}+Z_{1}=2+(4j)+(4-2j)=6+2j=6.32{\angle}18.43^{o}\,}}$

فيكون التيار العقدي ${\displaystyle{\displaystyle I_{1}:I_{1}={\frac{V}{Z_{E}}}={\frac{20{\angle}0^{o}}{6.32{\angle}18.43^{o}}}=3.165{\angle}-18.43^{o}=3-j\,}}$

من أجل حساب التيارين ${\displaystyle{\displaystyle I_{2}\,}}$ و${\displaystyle{\displaystyle I_{3}\,}}$ نستخدم قانون مقسم التيار، فنجد:

${\displaystyle{\displaystyle I_{3}=I_{1}{\frac{Z_{2}}{Z_{2}+Z_{3}}}=3.165{\angle}-18.43^{o}{\frac{5{\angle}0^{o}}{11.18{\angle}-63.43^{o}}}=1.415{\angle}45^{o}=1+j\,}}$

ومن أجل الحصول على التيار ${\displaystyle{\displaystyle I_{2}\,}}$ نطبق قانون كرشوف للتيارات فنجد:

${\displaystyle{\displaystyle I_{2}=I_{1}-I_{3}=(3-j)-(1+j)=2-2j=2.828{\angle}45^{o}\,}}$

الطلب الثاني: بما أن التيار والفلطية متوافقان في مقاومة، ففرق الصفحة بينهما معدوم (راجع علاقة الاستطاعة التي مرت معنا)، فالاستطاعة المستهلكة هي جداء المقاومة في مربع طويلة التيار المنتج:

${\displaystyle{\displaystyle P=V_{\mathit{eff}}I_{\mathit{eff}}\cos(0^{o})=R{I_{\mathit{eff}}}^{2}\,}}$

في المقاومة ${\displaystyle{\displaystyle 2\omega\,}}$: ${\displaystyle{\displaystyle 2{I_{1}}^{2}=2\times 3.165^{2}\simeq 20W\,}}$

في المقاومة ${\displaystyle{\displaystyle 5\omega\,}}$: ${\displaystyle{\displaystyle 5{I_{3}}^{2}=5\times 2.828^{2}\simeq 40W\,}}$

الطلب الثالث:

الاستطاعة التفاعلية للمكثفة:${\displaystyle{\displaystyle Q_{c}=V_{\mathit{eff}}I_{\mathit{eff}}\sin-90^{o}=X_{c}{I_{\mathit{eff}}}^{2}\sin-90^{o}=-10\times 1.415^{2}\simeq-20{\mathit{VAR}}\,}}$

الاستطاعة التفاعلية للوشيعة:${\displaystyle{\displaystyle Q_{L}=X_{L}{I_{1}}^{2}\sin(90^{o})=4\times 3.165^{2}\simeq 40{\mathit{VAR}}\,}}$

وبالتالي الاستطاعة التفاعلية للدارة: ${\displaystyle{\displaystyle Q=Q_{c}+Q_{L}=20{\mathit{VAR}}\,}}$

الطلب الرابع: عامل استطاعة الدارة هو ${\displaystyle{\displaystyle\cos\phi=\cos(\theta_{1}-\theta_{2})\,}}$، أي هو جيب التمام لفرق الطور بين التيار والفلطية الكليين، وبما أن

${\displaystyle{\displaystyle Z_{E}={\frac{V}{I}}={\frac{V{\angle}\theta_{1}}{I{\angle}\theta_{2}}}=(V/I){\angle}(\theta_{1}-\theta_{2})=6.32{\angle}18.43\,}}$

فيكون عامل استطاعة الدارة: ${\displaystyle{\displaystyle\cos\phi=\cos(18.43^{o})\simeq 0.95\,}}$

الاستطاعة الكلية المستهلكة في الدارة: ${\displaystyle{\displaystyle P=V_{\mathit{eff}}I_{\mathit{eff}}\cos\phi=20\times 3.165\times 0.95\simeq 60W\,}}$

وهي تماما مجموع الاستطاعتين المستهلكتين في المقاومتين فقط. فالمكثفة والوشيعة المثاليتان عنصران لا يستهلكان الطاقة.

انتهت المسألة!

 الاستطاعة العقدية

ليكن لدينا عنصر فيه تيار متناوب${\displaystyle{\displaystyle I=I_{\mathit{eff}}{\angle}\beta\,}}$ ، والفلطية المطبقة هي${\displaystyle{\displaystyle V=V_{\mathit{eff}}{\angle}\alpha\,}}$ ، فتكون الاستطاعة المستهلكة:

${\displaystyle{\displaystyle P=V_{\mathit{eff}}I_{\mathit{eff}}\cos(\alpha-\beta)\,}}$ وحسب علاقة أويلر :${\displaystyle{\displaystyle re^{\mathit{jx}}=r(\cos x+j\sin x)\,}}$، فإن الاستطاعة هي القسم الحقيقي للعدد العقدي: ${\displaystyle{\displaystyle V_{\mathit{eff}}I_{\mathit{eff}}e^{j(\alpha-\beta)}\,}}$ أي

${\displaystyle{\displaystyle P={\mathit{Real}}[V_{\mathit{eff}}I_{\mathit{eff}}e^{j(\alpha-\beta)}]={\mathit{Real}}[(V_{\mathit{eff}}e^{j\alpha})(I_{\mathit{eff}}e^{-j\beta})]\,}}$

ولكن${\displaystyle{\displaystyle I_{\mathit{eff}}e^{-j\beta}=I_{\mathit{eff}}{\angle}-\beta\,}}$ ما هو إلا المرافق العقدي للتيار I أي: ${\displaystyle{\displaystyle I^{M}=I_{\mathit{eff}}e^{-j\beta}\,}}$، لأن مرافق أي عدد عقدي كما نعلم يعطى بالعلاقة: ${\displaystyle{\displaystyle(re^{j\theta})^{M}=re^{-j\theta}\,}}$. وبالتالي فالاستطاعة المستهلكة هي القسم الحقيقي لجداء الفلطية بالمرافق العقدي للتيار: ${\displaystyle{\displaystyle P={\mathit{Real}}[VI^{M}]\,}}$