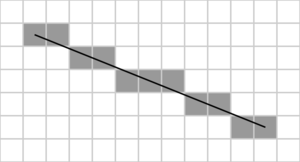
خوارزمية برزنهام لرسم مستقيم
خوارزمية بريزنهام لرسم مستقيم هي خوارزمية تحدد أي النقاط في الفضاء من البعد n يجب أن يرسم من أجل الحصول على تقريب مناسب للخط المستقيم بين نقطتين معرفتين. تعتبر واحدة من خوارزميات رسم المستقيم التي تستخدم هذه الخوارزمية عادة في الرسم على شاشة الحاسب، وذلك لأنها تعتمد على عمليات لا تستهلك الكثير من قدرات الحاسب، كجمع الأعداد الصحيحة، وطرحها وعمليات نقل البتات. وتعتبر هذه الخوارزمية واحدة من أوائل الخوارزميات التي تم تطويرها في الرسوميات الحاسوبية.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
تاريخ
تم تطوير هذه الخوارزمية من قبل جاك بريزنهام عام 1962 في شركة أي بي إم. كما تم تعديل هذه الخوارزمية في وقت لاحق لكي تتمكن من رسم دوائر.
الخوارزمية
سيستخدم افتراض أن قيمة إحداثيات النقاط تزداد بالاتجاه نحو الأسفل واليمين، وسوف يستخدم الإحداثيات الصحيحة لهذه النقاط. نعرف إحداثيات نقطتي المستقيم على الشكل (x0, y0) و(x1, y1) حيث الإحداثية الأولى من الثنائية تمثل الأعمدة والثانية تمثل الصفوف.
سوف تعرف الخوارزمية بالبداية من أجل ثمانية يكون فيها قطعة الخط المستقيم تتجه باتجاه الأسفل واليمين (x0≤x1 and y0≤y1 )، ويكون مسقطها الأفقي أطول من مسقطها العمودي (أو أن ميل المستقيم يكون أقل من 1 وأكبر من 0). في هذه الثمانية فإنه من أجل أي عمود x بين و ، يوجد عمود وحيد y (يتم حسابه من قبل الخوارزمية) يحتوي النقطة الواقعة على المستقيم، بينما كل صف بين و ربما يحتوي على بضعة نقاط مرسومة.
تختار الخوارزمية قيمة y الصحيحة المقابلة لمركز النقطة الأقل إلى أقرب كسر y من أجل قيمة مساوية ل x، وبهذا وعند العمود التالي من الممكن لقيمة y أن تبقى على حالها أو أن تزيد بمقدار 1. وتكون المعادلة العامة للمستقيم بدلالة نقطتي النهاية معطاة بالعلاقة:
وعلى اعتبار أننا نعرف العمود x يعطى صف النقطة y بتدوير الكمية التالية إلى أقرب عدد صحيح:
يعتمد الميل على إحدثيات نقاط النهاية فقط ومن الممكن إعادة حسابه بشكل مسبق، والقيم المثالية ل y بشكل تتابع من الممكن حسابها بالبدء عند وإضافة الميل بشكل متكرر.
في الكود البرمجي التالي، يقوم التابع plot(x,y) برسم النقاط وتعطي abs القيمة المطلقة:
function line(x0, x1, y0, y1)
int deltax := x1 - x0
int deltay := y1 - y0
real error := 0
real deltaerr := deltay / deltax // Assume deltax != 0 (line is not vertical),
// note that this division needs to be done in a way that preserves the fractional part
int y := y0
for x from x0 to x1
plot(x,y)
error := error + deltaerr
if abs(error) ≥ 0.5 then
y := y + 1
error := error - 1.0