خط اويلر

خط أويلر (الأحمر) هو خط مستقيم يمر عبر مركز الكتلة (برتقالي) ، والمركز العمودي (أزرق) ، والمركز المحيطي (أخضر) ومركز دائرة النقاط التسع (أحمر).

في الهندسة الرياضية، خط أويلر، نسبةً إلى ليونهارت أويلر، هو خط من أي مثلث غير متساوي الأضلاع، خط مركزي للمثلث، ويمر عبر عدة نقاط مهمة محددة من المثلث، بما في ذلك المركز العمودي، والمركز المحيطي، ومركز الكتلة، ونقطة إكستر، ومركز دائرة النقاط التسعة للمثلث.

يمتد مفهوم خط أويلر للمثلثات إلى خط أويلر للأشكال الأخرى، مثل الرباعي ورباعي السطوح .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

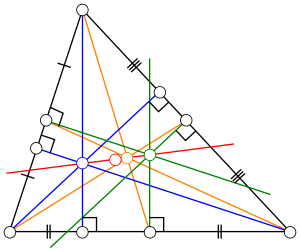
 مراكز المثلث على خط أويلر

 المراكز

أظهر أويلر في عام 1765 أنه في أي مثلث، المركز العمودي والمركز المحيطي ومركز الكتلة يقعون على خط واحد (متسامتة). تنطبق هذه الخاصية أيضًا على أي مركز مثلث آخر، مع أنّ مركز دائرة النقاط التسعة لم يُعرف في زمن أويلر. في المثلثات متساوية الأضلاع، تتطابق هذه النقاط الأربعة، لكن في أي مثلث آخر تكون جميعها متميزة عن بعضها البعض، ويُحَدَّدُ خط أويلر بأي اثنتين منها.

تشمل النقاط البارزة الأخرى الواقعة على خط أويلر نقطة دي لونجتشامبس ونقطة شيفلر ونقطة إكستر ومنظار جوسارد . ومع ذلك، فإن المركز الداخلي، عمومًا، لا يقع على خط أويلر؛ إنه موجود على خط أويلر فقط في المثلثات متساوية الساقين، التي يتطابق فيها خط أويلر مع محور التماثل للمثلث ويحتوي على جميع مراكز المثلث.

المثلث المماسي لمثلث مرجعي هو المماس إلى الدائرة المحيطة بالمثلث المرجعي عند رؤوس المثلث المرجعي. يقع المركز المحيطي للمثلث المماسي على خط أويلر للمثلث المرجعي. ^{:p. 447 :p.104,#211;p.242,#346}يقع مركز المشابهة للمثلثات المماسية والعمودية أيضًا على خط أويلر. ^{:p. 447 :p. 102}

 إثبات اتجاهي

افترض أن $ABC$ مثلث. إثبات حقيقة أن المركز المحيطي $O$، مركز الكتلة $G$ والمركز العمودي $H$ متسامتة تعتمد على المتجهات الحرة. نبدأ بذكر المتطلبات الأساسية. أولًا، $G$ تحقق العلاقة

${\vec {GA}}+{\vec {GB}}+{\vec {GC}}=0.$

هذا يأتي من حقيقة أن المحاور الكتلية لـ$G$ ${\frac {1}{3}}:{\frac {1}{3}}:{\frac {1}{3}}$. إضافةً إلى ذلك، مشكلة سيلفستر هي

${\vec {OH}}={\vec {OA}}+{\vec {OB}}+{\vec {OC}}.$

الآن، باستخدام إضافة المتجهات، نستنتج أن

${\vec {GO}}={\vec {GA}}+{\vec {AO}}\,{\mbox{(in triangle }}AGO{\mbox{)}},\,{\vec {GO}}={\vec {GB}}+{\vec {BO}}\,{\mbox{(in triangle }}BGO{\mbox{)}},\,{\vec {GO}}={\vec {GC}}+{\vec {CO}}\,{\mbox{(in triangle }}CGO{\mbox{)}}.$

بإضافة هذه العلاقات الثلاث، حد بعد حد، نحصل على

$3\cdot {\vec {GO}}=\left(\sum \limits _{\scriptstyle {\rm {cyclic}}}{\vec {GA}}\right)+\left(\sum \limits _{\scriptstyle {\rm {cyclic}}}{\vec {AO}}\right)=0-\left(\sum \limits _{\scriptstyle {\rm {cyclic}}}{\vec {OA}}\right)=-{\vec {OH}}.$

ختامًا، $3\cdot {\vec {OG}}={\vec {OH}}$، وهكذا النقاط الثلاثة $O$ و $G$ و $H$ (بهذا الترتيب) على خط واحد.

في كتاب دوري Dörrie، وضع خط أويلر ومشكلة سيلفستر معًا في إثبات واحد. ومع ذلك، تعتمد معظم براهين مشكلة سيلفستر على الخصائص الأساسية للمتجهات الحرة، بصرف النظر عن خط أويلر.

 المسافات بين المراكز

على خط أويلر، يقع مركز الكتلة G بين المركز المحيطي O و والمركز العمودي H و يبعد ضعف البعد، الذي يبعده عن المركز المحيطي، عن المركز العمودي: ^:p.102

$GH=2GO;$

$OH=3GO.$

القطعة GH قطر لدائرة، المركزين العمودي و الكتلي نهايتي قطر فيها.

يقع المركز N لدائرة النقاط التسعة على خط أويلر في المنتصف بين المركز العمودي و المركز المحيطي:

$ON=NH,\quad OG=2\cdot GN,\quad NH=3GN.$

لذا، يمكن إعادة وضع خط أويلر على خط أعداد حيث المركز المحيطي O في الموقع 0، ومركز الكتلة G عند 2t، ومركز دائرة النقاط التسعة عند 3t، والمركز العمودي H عند 6t عامل المقياس t.

إضافةً إلى ذلك، فإن المسافة المربعة بين مركز الكلتة والمركز المحيطي على طول الخط أويلر أقل من مربع نصف القطر المحيطي R ² بقدر مساوي تسع مجموع مربعات الأضلاعa، b، c: ^:p.71

$GO^{2}=R^{2}-{\tfrac {1}{9}}(a^{2}+b^{2}+c^{2}).$

بالإضافة إلى، ^:p.102

$OH^{2}=9R^{2}-(a^{2}+b^{2}+c^{2});$

$GH^{2}=4R^{2}-{\tfrac {4}{9}}(a^{2}+b^{2}+c^{2}).$

 التمثيل

 المعادلة

افترض أن A، B ، C تشير إلى زوايا رؤوس المثلث المرجعي، وافترض أن x: y : z نقطة متغيرة في إحداثيات خطية ثلاثية؛ عندها تكون معادلة خط أويلر

$\sin(2A)\sin(B-C)x+\sin(2B)\sin(C-A)y+\sin(2C)\sin(A-B)z=0.$

معادلة لخط أويلر في إحداثيات كتلية $\alpha :\beta :\gamma$ هو

$(\tan C-\tan B)\alpha +(\tan A-\tan C)\beta +(\tan B-\tan A)\gamma =0.$

 تمثيل بارامتري

يمكن تمثيل خط أويلر بواسطة المعامل t ، بدءًا من المركز المحيطي (بإحداثيات خطية ثلاثية $\cos A:\cos B:\cos C$) والمركز العمودي (ذو الثلاث خطوط $\sec A:\sec B:\sec C=\cos B\cos C:\cos C\cos A:\cos A\cos B$). تُعطى كل نقطة على خط أويلر، باستثناء المركز العمودي، بواسطة الإحداثيات الخطية الثلاثية

$\cos A+t\cos B\cos C:\cos B+t\cos C\cos A:\cos C+t\cos A\cos B$

تشكلت كتركيبة خطية من الإحداثيات الخطية الثلاثية لهاتين النقطتين، بالنسبة للمعامل t.

على سبيل المثال:

• المركز المحيطي له الإحداثيات الخطية الثلاثية $\cos A:\cos B:\cos C,$ المقابلة لقيمة المعامل $t=0.$
• مركز الكتلة له الإحداثيات الخطية الثلاثية$\cos A+\cos B\cos C:\cos B+\cos C\cos A:\cos C+\cos A\cos B$، المقابلة لقيمة المعامل $t=1.$
• مركز دائرة النقاط التسع له الإحداثيات الثلاثية$\cos A+2\cos B\cos C:\cos B+2\cos C\cos A:\cos C+2\cos A\cos B,$ المقابلة لقيمة المعلمة $t=2.$
• نقطة دي لونجتشامب لها الإحداثيات الخطية الثلاثية$\cos A-\cos B\cos C:\cos B-\cos C\cos A:\cos C-\cos A\cos B$ المقابلة لقيمة المعامل $t=-1.$

 الميل

في نظام الإحداثيات الديكارتية، نشير إلى ميول أضلاع المثلث بالرموز $m_{1},$$m_{2},$$m_{3},$ ونشير إلى ميل خط أويلر بالرمز $m_{E}$. وترتبط هذه الميول وفقًا لـ ^{:Lemma 1}

$m_{1}m_{2}+m_{1}m_{3}+m_{1}m_{E}+m_{2}m_{3}+m_{2}m_{E}+m_{3}m_{E}$

$+3m_{1}m_{2}m_{3}m_{E}+3=0.$

لذا فإنّ ميل خط أويلر (إذا كان محدودًا) يمكن التعبير عنه من حيث ميل الأضلاع كـ

$m_{E}=-{\frac {m_{1}m_{2}+m_{1}m_{3}+m_{2}m_{3}+3}{m_{1}+m_{2}+m_{3}+3m_{1}m_{2}m_{3}}}.$

فضلًا على ذلك، فإن خط أويلر يوازي الضلع BC في المثلث الحاد إذا وفقط إذا ^:p.173$\tan B\tan C=3$.

 العلاقة بالمثلثات المتساوية الأضلاع المدرجة

المحل الهندسي لمراكز الكتلة للمثلثات متساوية الأضلاع المدرجة في مثلث معين ينشئ بواسطة خطين عموديين على خط أويلر للمثلث المحدد. ^{:Coro. 4}

 في مثلثات خاصة

 مثلث قائم

في المثلث القائم ، يتطابق خط أويلر مع المتوسط على الوتر — أي أنه يمر عبر كل من الرأس القائم ونقطة المنتصف في الضلع المقابل لذلك الرأس. هذا لأن المركز العمودي للمثلث القائم، نقطة تقاطع ارتفاعاته، يقع على الرأس القائمة بينما يقع مركزه المحيطي، نقطة تقاطع منصفات أضلاعه العمودية، على نقطة منتصف الوتر.

 مثلث متساوي الساقين

يتطابق خط أويلر لمثلث متساوي الساقين مع محور تماثله. في المثلث متساوي الساقين، المركز الداخلي يقع على خط أويلر.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 مثلث المتوسطات المتناسبة

خط أويلر في مثلث المتوسطات المتناسبة (المثلث الذي متوسطاته متناسبة مع الأضلاع، على التوالي.) عمودي على أحد المتوسطات.

 أنظمة المثلثات ذات خطوط أويلر المتطابقة

اعتبر المثلث ABC بنقطتي F ₁ نقطة فيرما و F ₂. خطوط أويلر للمثلثات العشرة ذات الرؤوس المختارة من A و B و C و F ₁ و F ₂ تتقاطع عند مركز الكتلة للمثلث ABC .

خطوط أويلر للمثلثات الأربعة المتشكلة بنظام مركزي عمودي (مجموعة من أربع نقاط حيث كل منها المركز العمودي للمثلث المتشكل بالنقاط الثلاث الأخرى) تتقاطع عند مركز دائرة النقاط التسعة المشترك لجميع المثلثات. ^:p.111

 التعميمات

 المضلع الرباعي

في المحدب الرباعي، المركز شبه العمودي H، و" مركز كتلة المساحة" G، والمركز شبه المحيطي O متسامتة، على هذا الترتيب، على خط أويلر، وHG = 2 GO.

 رباعي السطوح

رباعي السطوح هو جسم ثلاثي الأبعاد يحده أربعة أوجه مثلثة. سبعة خطوط مرتبطة برباعي الوجوه تتقاطع عند مركز كتلته، تتقاطع مستوياته المٌنصِفة الستة عند نقطة مونجي، والكرة المحيطة تمر عبر جميع الرؤوس، ومركزها المركز المحيطي. تحدد هذه النقاط "خط أويلر" لرباعي الوجوه المناظر لخط المثلث. مركز الكتلة هو نقطة المنتصف بين نقطة مونجي و المركز المحيطي على طول هذا الخط. يقع مركز كرة النقاط الاثنى عشرة أيضًا على خط أويلر.

 عديد الأبعاد المبسط

عديد الأبعاد المبسط هو عديد أبعاد كل جوانبه مبسطة. على سبيل المثال، كل مضلع هو عديد أبعاد مبسط. خط أويلر المرتبط بمثل عديد الأبعاد هو الخط المحدد بمركز الكتلة و المركز المحيطي للكتلة. هذا التعريف لخط أويلر يعمم ذلك المذكور أعلاه.

لنفترض أن $P$ مضلع. خط أويلر $E$ حساس لتماثلات $P$ بالطرق التالية:

1. لو $P$ له خط التماثل الانعكاسي $L$ ، من ثم $E$ إما $L$ أو نقطة على $L$.

2. لو $P$ له مركز التماثل الدوراني $C$ ، من ثم $E=C$ .

3. إذا كانت كل جوانب $P$ متساوية في الطول ، إذًا $E$ متعامد مع الجانب الأخير.

 الإنشاءات ذات الصلة

قطع كيبرت المكافئ لمثلث هو القطع المكافئ الفريد المماس للأضلاع المثلث (بعد مد اثنين منهم ) و خط أويلر الدليل له . ^{:p. 63}

 انظر أيضًا

• خط سيمسون.
• دائرة.
• دوائر داخلية وخارجية لمثلث.

 وصلات خارجية

• قالب:ماثوورلد

قالب:دائرة