تعتم طرفي

الشمس المعتم طرفها - صورة للشمس في الضوء المرئي تُظهر أثر التعتم الطرفي كانخفاض في الشدة باتجاه حافة أو "طرف" القرص الشمسي.

التعتم الطرفي Limb darkening أو إظلام الحافة ظاهرة فلكية تبدو فيها حافة الشمس أقل لمعانا من مركز قرصها . تحدث هذة الظاهرة نتيجة الضوء الذى يشاهد على طرف الشمس المنطلق من أعالى الكرة الضوئية ذات الدرجة الحرارية الاقل.

حالة محوَّلة إلى المثالية من التعتم الطرفي. الحد الخارجي هو نصف القطر الذي عنده لا يتم امتصاص الفوتونات المنبعثة من النجم. L  هي المسافة التي يكون عندها العمق الضوئي مساوياً للوحدة. فوتونات درجات الحرارة العالية المنبعثة من A ستفلت بالكاد من النجم، كما ستفلت فوتونات درجات الحرارة المنخفضة المنبعثة من B.

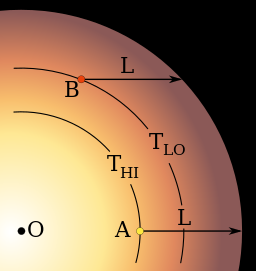
هناك تعتم طرفي في النجوم أيضا ويمكن مشاهدة ذلك في بعض الحالات الخاصة كما في المتغيرات الكسوفية لأن النجوم تظهر نقطية الشكل .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 حساب التعتم الطرفي

هندسة التعتم الطرفي. النجم متمركز في O  وله نصف قطر R . الراصد عند النقطة P  على بعد r  من مركز النجم، وينظر إلى النقطة S  على سطح النجم. من وجهة نظر الراصد، S  هي على زاوية θ من خط يمر عبر مركز النجم، وحافة أو طرف النجم على زاوية Ω.

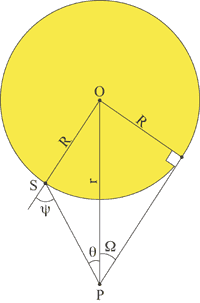
In the figure on the right, as long as the observer at point P is outside the stellar atmosphere, the intensity seen in the direction θ will be a function only of the angle of incidence ψ. This is most conveniently approximated as a polynomial in cos(ψ)

${\frac {I(\psi )}{I(0)}}=\sum _{k=0}^{N}a_{k}\,{\textrm {cos}}^{k}(\psi )$

where I(ψ) is the intensity seen at P along a line of sight forming angle ψ with respect to the stellar radius, and I(0) is the central intensity. It can be seen that in order that the ratio be unity for ψ=0, we must have:

$\sum _{k=0}^{N}a_{k}=1$

For example, for a Lambertian radiator (no limb darkening) we will have all a_k=0 except a₀=1. As another example, for the sun at 550 nm, the limb darkening is well expressed by N=2 and

$a_{0}=1-a_{1}-a_{2}\,$

$a_{1}=0.93\,$

$a_{2}=-0.23\,$

(See Cox, 2000). Note - the equation for limb darkening is sometimes more conveniently written as:

${\frac {I(\psi )}{I(0)}}=1+\sum _{k=1}^{N}A_{k}\,(1-\cos(\psi ))^{k}$

which now has N  independent coefficients rather than N+1  coefficients which must sum to unity.

We can convert from ψ to θ using the relationship:

$\cos(\psi )={\frac {\sqrt {\cos ^{2}(\theta )-\cos ^{2}(\Omega )}}{\sin(\Omega )}}$

where Ω is the angle from the observer to the limb of the star.

The above approximation can be used to derive an analytic expression for the ratio of the mean intensity to the central intensity. The mean intensity I_m is the integral of the intensity over the disk of the star divided by the solid angle subtended by the disk:

$I_{m}={\frac {\int I(\psi )d\omega }{\int d\omega }}$

where dω=sin(θ)dθdφ is a solid angle element and the integrals are over the disk: 0≤φ≤2π and 0≤θ≤Ω. Although this equation can be solved analytically, it is rather cumbersome. However, for an observer at infinite distance from the star, the above equation simplifies to:

${\frac {I_{m}}{I(0)}}=2\sum _{k=0}^{N}{\frac {a_{k}}{k+2}}$

 المصادر

• مؤمن, عبد الأمير (2006). قاموس دار العلم الفلكي. بيروت، لبنان: دار العلم للملايين. {{cite book}}: Cite has empty unknown parameter: |طبعة أولى coauthors= (help)

• Billings, Donald E. (1966). A Guide to the Solar Corona. Academic Press, New York.

• Cox, Arthur N. (ed) (2000). Allen's Astrophysical Quantities (14th ed. ed.). Springer-Verlag, NY. ISBN 0-387-98746-0. {{cite book}}: |author= has generic name (help); |edition= has extra text (help)

• Milne, E.A. (1921). MNRAS. 81: 361–375. {{cite journal}}: Missing or empty |title= (help)

• Minnaert, M. (1930). Z.f. Ap. 1: 209. {{cite journal}}: Missing or empty |title= (help)

• Neckel, H. and Labs, D. (1994). "Solar Limb Darkening 1986-1990". Solar Physics. 153: 91–114. doi:10.1007/BF00712494.{{cite journal}}: CS1 maint: multiple names: authors list (link)

• van de Hulst, H. C. (1950). Bull. Astron. Inst. Netherlands. 11 (410): 135. {{cite journal}}: Missing or empty |title= (help)

• Steiner, O., Photospheric processes and magnetic flux tubes, (2007) [[1]]