تدوين أوه الكبيرة

مخطط ڤن يوضح العلاقة بين الأنواع المختلفة للتدوين المقارب

في الرياضيات وعلم الحاسوب، والمجالات ذات الصلة ، تدوين أوه الكبيرة big O notation (المعروف أيضا باسم big O notation، تدوين لانداو Landau notation، تدوين باخمان-لانداو Bachmann–Landau notation، والتدوين المقارب) يصف السلوك الحدي لتابع عندما يسعى الوسيط نحو قيمة معينة أو اللانهاية عادة باستخدام توابع أبسط. يميز تدوين أوه الكبيرة التوابع وفقا لمعدلات النمو لديها: فقد تمثل التوابع المختلفة وذات معدل النمو الواحد باستخدام تدوين أوه نفسه.

على الرغم من أنها طوّرت كجزء من الرياضيات البحتة ، فإن هذا التدوين كثيرا ما يستخدم الآن في تحليل الخوارزميات لوصف استهلاك خوارزمية ما للموارد التحسيبية: غالباً ما يعبر عن وقت التشغيل واستخدام الذاكرة في الحال الأسوأ أو الحال المتوسط من قبل خوارزمية ما بوصفهما تابعين للدخل بإستخدام تدوين أوه الكبيرة. هذا يسمح لمصممي خوارزمية التنبؤ بسلوك الخوارزميات، وتحديد الخوارزمية المناسبة للاستخدام من بين عدة خوارزميات، وبطريقة مستقلة عن بنيان الحاسوب أو معدل الساعة. وبما أنه في تدون أوه الكبيرة تهمل ثوابت مضروبة بوقت التشغيل، وتُتجاهل كفاءة الخوارزمية لأحجام منخفضة من المدخلات، فإن لا يكشف دائما أسرع خوارزمية بالنسبة للممارسة العملية أو بالنسبة لمجموعات من البيانات ذات أحجام عملية. لكن هذا النهج يظل فعالاً للغاية للتوصل إلى التدرج بين الخوارزميات المختلفة عندما تصبح أحجام المدخلات كبيرة.

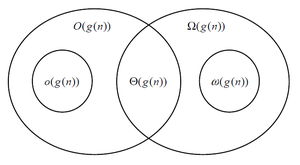
لا يعطي تدوين أوه الكبيرة لتابع موصف من خلاله تقدم سوى الحد الأعلى لمعدل نمو ذلك التابع. كما ترتبط بتدوين أوه الكبيرة تدوينات عدة، وذلك باستخدام الرموز o ، Ω ، ω ، وΘ ، لوصف أنواع أخرى من حدود معدلات النمو المقاربة. كما يستخدم تدوين أوه الكبيرة العديد من المجالات الأخرى لتقديم تقديرات مماثلة.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 التعريف الشكلي

ليكن لدينا التابعان f(x) و g(x) المعرفان على مجال فرعي ما من مجموعة الأعداد الحقيقة. نكتب:

$f(x)=O(g(x)){\mbox{ as }}x\to \infty \,$

إذا وفقط إذا، ومن أجل قيم كبيرة بما فيه الكفاية لـ x،كانت قيمة f(x) على الأكثر هي قيمة g(x) مضروبة بثابت ما.

هذا يعني، يكون f(x) = O(g(x)) إذا وفقط إذا وجد عدد حقيقي M وعدد حقيقي x₀ بحيث::$|f(x)|\leq \;M|g(x)|{\mbox{ for all }}x>x_{0}.$

In many contexts, the assumption that we are interested in the growth rate as the variable x goes to infinity is left unstated, and one writes more simply that f(x) = O(g(x)).

The notation can also be used to describe the behavior of f near some real number a (often, a = 0): we say

$f(x)=O(g(x)){\mbox{ as }}x\to a\,$

if and only if there exist positive numbers δ and M such that

$|f(x)|\leq \;M|g(x)|{\mbox{ for }}|x-a|<\delta .$

If g(x) is non-zero for values of x sufficiently close to a, both of these definitions can be unified using the limit superior:

$f(x)=O(g(x)){\mbox{ as }}x\to a\,$

if and only if

$\limsup _{x\to a}\left|{\frac {f(x)}{g(x)}}\right|<\infty .$

 Related asymptotic notations

Big O is the most commonly used asymptotic notation for comparing functions, although in many cases Big O may be replaced with Big Theta Θ for asymptotically tighter bounds. Here, we define some related notations in terms of Big O, progressing up to the family of Bachmann–Landau notations to which Big O notation belongs.

 Little-o notation

The relation $f(x)\in o(g(x))$ is read as "$f(x)$ is little-o of $g(x)$". Intuitively, it means that $g(x)$ grows much faster than $f(x)$. It assumes that f and g are both functions of one variable. Formally, it states

$\lim _{x\to \infty }{\frac {f(x)}{g(x)}}=0.$

Or alternatively:

Let f(x) and g(x) be two functions defined on some subset of the real numbers. One writes

$f(x)=o(g(x)){\mbox{ as }}x\to \infty \,$

if and only if, for each positive constant M, f(x) is at most M multiplied by g(x) in absolute value, for each x, which is large enough. That is, f(x) = o(g(x)) if and only if, for every $M>0$, there exists a constant x₀, such that

$|f(x)|\leq \;M|g(x)|{\mbox{ for all }}x>x_{0}.$

Note the difference between the earlier formal definition for the Big-O notation, and the present definition of little-o: while the former has to be true for at least one constant M the latter must hold for every positive constant.

For example,

• $2x\in o(x^{2})\,\!$
• $2x^{2}\not \in o(x^{2})$
• $1/x\in o(1)$

Little-o notation is common in mathematics but rarer in computer science. In computer science the variable (and function value) is most often a natural number. In mathematics, the variable and function values are often real numbers. The following properties can be useful:

• $o(f)+o(f)\subseteq o(f)$
• $o(f)o(g)\subseteq o(fg)$
• $o(o(f))\subseteq o(f)$
• $o(f)\subset O(f)$ (and thus the above properties apply with most combinations of o and O).

As with big O notation, the statement "$f(x)$ is $o(g(x))$" is usually written as $f(x)=o(g(x))$, which is a slight abuse of notation.

 Family of Bachmann–Landau notations

Notation	Name	Intuition	As $n\to \infty$, eventually...	Definition
$f(n)\in O(g(n))$	Big Omicron; Big O; Big Oh	$f$ is bounded above by $g$ (up to constant factor) asymptotically	$|f(n)|\leq g(n)\cdot k$ for some k	$\exists k>0,n_{0}\;\forall n>n_{0}\;|f(n)|\leq |g(n)\cdot k|$ or $\exists k>0,n_{0}\;\forall n>n_{0}\;f(n)\leq g(n)\cdot k$
$f(n)\in \Omega (g(n))$ (Note that papers in number theory have been increasingly and widely using this same notation, since the beginning of the 20th century, in the weaker sense that f = o(g) is false)	Big Omega	$f$ is bounded below by $g$ (up to constant factor) asymptotically	$|f(n)|\geq g(n)\cdot k$ for some k	$\exists k>0,n_{0}\;\forall n>n_{0}\;g(n)\cdot k\leq |f(n)|$
$f(n)\in \Theta (g(n))$	Big Theta	$f$ is bounded both above and below by $g$ asymptotically	$|g(n)|\cdot k_{1}\leq |f(n)|\leq |g(n)|\cdot k_{2}$ for some k1, k2	$\exists k_{1},k_{2}>0,n_{0}\;\forall n>n_{0}$ $|g(n)|\cdot k_{1}\leq |f(n)|\leq |g(n)|\cdot k_{2}$
$f(n)\in o(g(n))$	Small Omicron; Small O; Small Oh	$f$ is dominated by $g$ asymptotically	$|f(n)|\leq |g(n)|\cdot \varepsilon$ for every $\varepsilon$	$\forall \varepsilon >0\;\exists n_{0}\;\forall n>n_{0}\;|f(n)|\leq |g(n)\cdot \varepsilon |$
$f(n)\in \omega (g(n))$	Small Omega	$f$ dominates $g$ asymptotically	$|f(n)|\geq |g(n)|\cdot k$ for every k	$\forall k>0\;\exists n_{0}\;\forall n>n_{0}\;|g(n)\cdot k|\leq |f(n)|$
$f(n)\sim g(n)\!$	on the order of; "twiddles"	$f$ is equal to $g$ asymptotically	$f(n)/g(n)\to 1$	$\forall \varepsilon >0\;\exists n_{0}\;\forall n>n_{0}\;|{f(n) \over g(n)}-1|<\varepsilon$

Bachmann–Landau notation was designed around several mnemonics, as shown in the As $n\to \infty$, eventually... column above and in the bullets below. To conceptually access these mnemonics, "omicron" can be read "o-micron" and "omega" can be read "o-mega". Also, the lower-case versus capitalization of the Greek letters in Bachmann–Landau notation is mnemonic.

• The o-micron mnemonic: The o-micron reading of $f(n)\in O(g(n))$ and of $f(n)\in o(g(n))$ can be thought of as "O-smaller than" and "o-smaller than", respectively. This micro/smaller mnemonic refers to: for sufficiently large input parameter(s), $f$ grows at a rate that may henceforth be less than $cg$ regarding $g\in O(f)$ or $g\in o(f)$.
• The o-mega mnemonic: The o-mega reading of $f(n)\in \Omega (g(n))$ and of $f(n)\in \omega (g(n))$ can be thought of as "O-larger than". This mega/larger mnemonic refers to: for sufficiently large input parameter(s), $f$ grows at a rate that may henceforth be greater than $cg$ regarding $g\in \Omega (f)$ or $g\in \omega (f)$.
• The upper-case mnemonic: This mnemonic reminds us when to use the upper-case Greek letters in $f(n)\in O(g(n))$ and $f(n)\in \Omega (g(n))$: for sufficiently large input parameter(s), $f$ grows at a rate that may henceforth be equal to $cg$ regarding $g\in O(f)$.
• The lower-case mnemonic: This mnemonic reminds us when to use the lower-case Greek letters in $f(n)\in o(g(n))$ and $f(n)\in \omega (g(n))$: for sufficiently large input parameter(s), $f$ grows at a rate that is henceforth inequal to $cg$ regarding $g\in O(f)$.

Aside from Big O notation, the Big Theta Θ and Big Omega Ω notations are the two most often used in computer science; the Small Omega ω notation is rarely used in computer science.

Informally, especially in computer science, the Big O notation often is permitted to be somewhat abused to describe an asymptotic tight bound where using Big Theta Θ notation might be more factually appropriate in a given context. For example, when considering a function $T(n)=73n^{3}+22n^{2}+58$, all of the following are generally acceptable, but tightnesses of bound (i.e., bullets 2 and 3 below) are usually strongly preferred over laxness of bound (i.e., bullet 1 below).

1. T(n) = O(n¹⁰⁰), which is identical to T(n) ∈ O(n¹⁰⁰)
2. T(n) = O(n³), which is identical to T(n) ∈ O(n³)
3. T(n) = Θ(n³), which is identical to T(n) ∈ Θ(n³).

The equivalent English statements are respectively:

1. T(n) grows asymptotically no faster than n¹⁰⁰
2. T(n) grows asymptotically no faster than n³
3. T(n) grows asymptotically as fast as n³.

So while all three statements are true, progressively more information is contained in each. In some fields, however, the Big O notation (bullets number 2 in the lists above) would be used more commonly than the Big Theta notation (bullets number 3 in the lists above) because functions that grow more slowly are more desirable. For example, if $T(n)$ represents the running time of a newly developed algorithm for input size $n$, the inventors and users of the algorithm might be more inclined to put an upper asymptotic bound on how long it will take to run without making an explicit statement about the lower asymptotic bound.

 Extensions to the Bachmann–Landau notations

Another notation sometimes used in computer science is Õ (read soft-O): f(n) = Õ(g(n)) is shorthand for f(n) = O(g(n) log^k g(n)) for some k. Essentially, it is Big O notation, ignoring logarithmic factors because the growth-rate effects of some other super-logarithmic function indicate a growth-rate explosion for large-sized input parameters that is more important to predicting bad run-time performance than the finer-point effects contributed by the logarithmic-growth factor(s). This notation is often used to obviate the "nitpicking" within growth-rates that are stated as too tightly bounded for the matters at hand (since log^k n is always o(n^ε) for any constant k and any ε > 0).

The L notation, defined as

$L_{n}[\alpha ,c]=O\left(e^{(c+o(1))(\ln n)^{\alpha }(\ln \ln n)^{1-\alpha }}\right),$

is convenient for functions that are between polynomial and exponential.

 انظر أيضاً

• Asymptotic expansion: Approximation of functions generalizing Taylor's formula
• Asymptotically optimal: A phrase frequently used to describe an algorithm that has an upper bound asymptotically within a constant of a lower bound for the problem
• Limit superior and limit inferior: An explanation of some of the limit notation used in this article
• Nachbin's theorem: A precise method of bounding complex analytic functions so that the domain of convergence of integral transforms can be stated
• Big O in probability notation : O_p,o_p

 قراءة متقدمة

• Paul Bachmann. Die Analytische Zahlentheorie. Zahlentheorie. pt. 2 Leipzig: B. G. Teubner, 1894.
• Edmund Landau. Handbuch der Lehre von der Verteilung der Primzahlen. 2 vols. Leipzig: B. G. Teubner, 1909.
• G. H. Hardy. Orders of Infinity: The 'Infinitärcalcül' of Paul du Bois-Reymond, 1910.
• Marian Slodicka (Slodde vo de maten) & Sandy Van Wontergem. Mathematical Analysis I. University of Ghent, 2004.
• Donald Knuth. The Art of Computer Programming, Volume 1: Fundamental Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89683-4. Section 1.2.11: Asymptotic Representations, pp. 107-123.
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 3.1: Asymptotic notation, pp. 41–50.
• Michael Sipser (1997). Introduction to the Theory of Computation. PWS Publishing. ISBN 0-534-94728-X. Pages 226–228 of section 7.1: Measuring complexity.
• Jeremy Avigad, Kevin Donnelly. Formalizing O notation in Isabelle/HOL
• Paul E. Black, "big-O notation", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed., U.S. National Institute of Standards and Technology. 11 March 2005. Retrieved December 16, 2006.
• Paul E. Black, "little-o notation", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed., U.S. National Institute of Standards and Technology. 17 December 2004. Retrieved December 16, 2006.
• Paul E. Black, "Ω", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed., U.S. National Institute of Standards and Technology. 17 December 2004. Retrieved December 16, 2006.
• Paul E. Black, "ω", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed., U.S. National Institute of Standards and Technology. 29 November 2004. Retrieved December 16, 2006.
• Paul E. Black, "Θ", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed., U.S. National Institute of Standards and Technology. 17 December 2004. Retrieved December 16, 2006.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 روابط خارجية

• Introduction to Asymptotic Notations