تأثير زيمان

شق زيمان للمستوى 5s من Rb-87، بما في ذلك شق البنى الدقيقة وشديدة الدقة. هنا F = J + I، حيث I هي المغزل النووي. (فلـ Rb-87، فإن I = 3/2)

تأثير زيمان Zeeman effect لاحظ عالم الطبيعة الهولندي پيتر زيمان ظاهرة زيمان أو تأثير زيمان لأول مرة عام 1896. وهي تجزؤ خطوط الطيف عندما يوضع مصدر للضوء في مجال مغنطيسي. وتنشأ خطوط الطيف الضوئي عندما تنتقل إلكترونات الذرَّة من مستوى طاقة إلى مستوى طاقة آخر. ويشير نمط خطوط الطيف إلى مستويات الطاقة بالذرات، لأن الخطوط تتجزأ عندما تدخل الذرات في مجال مغنطيسي. وتفيد ظاهرة زيمان أن مستويات الطاقة بالذرَّة قد تغيَّرت.

ولم يدرك العلماء تمام الإدراك مدى أهمية ظاهرة زيمان حتى عشرينيات القرن العشرين حين اكتشفت نظرية ميكانيكا الكم. ويستطيع علماء الفيزياء أن يدرسوا الخصائص المغنطيسية للذرات والإلكترونات الموجودة بها من خلال ملاحظة خطوط الطيف المتجزئة. وتستخدم الظاهرة أيضًا في دراسة الجزيئات والنويات.

وهذا التأثير مشابه لتأثير آخر يسمى تأثير شتارك وهو انشقاق خطوط الطيف إلي عدة خطوط في حالة تعرض المصدر لمجال كهربائي. ويستخدم تأثير زيمان في تطبيقات عديدة في مطياف الرنين المغناطيسي، ومطياف رنين الدوران المغزلي للإلكترون، وفي التصوير بالرنين المغناطيسي (MRI). وكثيرا ما يستخدم تأثير زيمان للتعيين الدقيق للأطياف الامتصاصية للعناصر. وفي حالة قياس خطوط الطيف الامتصاصي، يسمى بتأثير زيمان العكسي.

رسم يوضح تأثير زيمان

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 مقدمة

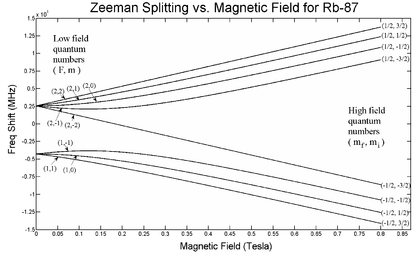
توجد في الذرات توزيعات مختلة للإلكترونات لها طاقة محددة واحدة . لذلك تظهر عدة قفزات للإلكترونات متماثلة علي هيئة خط واحد في الطيف . وفي وجود مجال مغناطيسي خارجي تنشق تلك التوزيعات ، حيث يتآثر كل منها مع المجال المغناطيسي بطريقة مختلفة بحسب الأعداد الكمومية لهذه التوزيعات، ذلك لأن الأعداد الكمومية المختلفة تُعبر عن حالات مختلفة لطاقتها وهي فروقا طفيفة . والنتيجة أنه بينما كانت هناك عدة توزيعات بنفس الطاقة ، نجد الآن عدة من مستويات الطاقة المختلفة قليلا ً تحت وطأة المجال المغناطيسي ، وهي تؤدي إلي انشقاق الخط الطيفي الواحد إلى عدة خطوط .

وطبقا للرسم التوضيحي ، تتسم التوزيعات a, b, c بحالة واحدة للطاقة ، كا ينطبق هذا علي التوزيعات d, e, f التي توجد في حالة طاقة محددة منخفضة عن حالة a, b, c . وفي وجود المجال المغناطيسي تنشق مستويات الطاقة . وينتج عن ذلك انه بينما كان يظهر لنا الانتقال من a, b, c إلى d, e, f في خط واحد ، يصبح لدينا عدة خطوط بسبب وجود عدة من الإنتقالات الممكنة بين a, b, c و d, e, f . ولكن لا يمكن للإلكترون القفز (الانتقال) إلى جميع المستويات المنخفضة d, e, f بلا اثتثناء ، وإنما هو محكوم بقفزات مسموحة وأخرى غير مسموحة ، بحسب قاعدة لذلك (انظر أسفله).

ونظرا لأن مقدار الانشقاق في خطوط الطيف تتناسب تناسباً طرديا ً مع شدة المجال المغناطيسي الخارجي ، يستخدم علماء الفلك تـاثير زيمان في قياس المجالات المغناطيسية للشـمس والنجوم الأخرى ومقارنتها.

 مثال : الإنتقال الخاص بخط لايمان-ألفا في الهيدروجين

يشتمل الانتقال المنتمي لخط لايمان-ألفا في الإيدروجين في وجود الارتباط المغزلي-المداري، على الانتقالات التالية:

$2P_{1/2}\to 1S_{1/2}$ و $2P_{3/2}\to 1S_{1/2}$ .

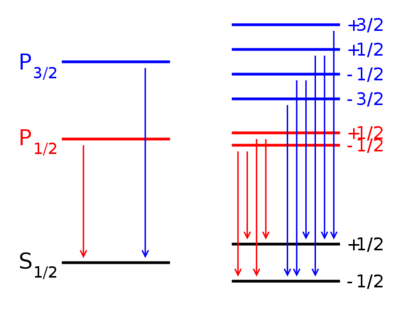
في وجود مجال مغناطيسي خارجي تنشق كل من الحالتين الكموميتين 1S_1/2 ; 2P_1/2 إلى مستويين اثنين وهما: $m_{j}=1/2,-1/2$ حيث $m_{j}$ عدد الكم المغناطيسي (وهو يحتوي في الحالة S على الدوران المغزلى للإلكترون فقط) ، وتنشق الحالة 2P_3/2 إلى أربعة مستويات للطاقة ($m_{j}=3/2,1/2,-1/2,-3/2$). معاملات-ج للاندي للمستويات الثلاث هي:

$g_{J}=2$ for $1S_{1/2}$ (j=1/2, l=0)

$g_{J}=2/3$ for $2P_{1/2}$ (j=1/2, l=1)

$g_{J}=4/3$ for $2P_{3/2}$ (j=3/2, l=1).

$m_{j}=3/2;1/2;-1/2;-3/2$ حيث أن l=1 للمدار P ، و $m_{j}$ في هذه الحالة هي محصلة الارطبات بين العزم المغزلي المغناطيسي للإلكترون والعزم المداري المغناطيسي ( انظر الشكل ).

ونلاحظ هنا :

• أن اتساع الانشقاق بين مستويات الطاقة مختلف باختلاف قيمة $m_{j}$ إذ أن مقدار الانشقاق يتناسب مع شدة تآثر الإلكترون مع المجال المغناطيسي الخارجي ، والذي يحدده معامل يسمي (g - factor) والذي يعتمد على $m_{j}$ . ونرى إلي اليسار انشقاق الحالة الكمومية P إلى مستويين , وهذا الانشقاق يحدث حتي في غياب المجال المغناطيسي الخارجي ، إذ أنه ناتج عن الارتباط المغزلي-المداري ، المذكور أعلاه. ونلاحظ علي يمين الرسم الانشقاق الإضافي الناشئ عن تأثير زيمان ، والذي يحدت تحت تأثير مجال مغناطيسي خارجي.

• أنه ليست جميع انتقالات الإلكترون من المستويات العليا إلى المستويات السفلى مسموح بها . فهناك انتقالات مسموحة ،وأخرى غير مسموحة ، و توجد قاعدة تتحكم في تصرف الإلكترون في هذا المجال.

 الاستخدامات

 الفيزياء الفلكية

Zeeman effect on a sunspot spectral line

George Ellery Hale was the first to notice the Zeeman effect in the solar spectra, indicating the existence of strong magnetic fields in sunspots. Such fields can be quite high, on the order of 0.1 Tesla or higher. Today, the Zeeman effect is used to produce magnetograms showing the variation of magnetic field on the sun.

 تبريد الليزر

The Zeeman effect is utilized in many Laser cooling applications such as a Magneto-optical trap and the Zeeman slower.

 انظر أيضاً

• ذرة
• تأثير شتارك
• magneto-optic Kerr effect
• Voigt effect
• Faraday effect
• Cotton-Mouton effect
• Polarization spectroscopy
• Magneto-optic Kerr effect
• Voigt effect
• Faraday effect
• Cotton-Mouton effect
• Polarization spectroscopy
• Zeeman energy
• Lamb shift
  • Electron configuration says at subshell p (l=1), there are 3 energy level ml=-1,0,1, but we see only two p1/2 and p3/2. for subshell s(l=0), there is only 1 energy level (ml=0), but here we have 2. l corresponding to fine structure, ml corresponding to hyperfine structure.

 الهامش

 تاريخي

• Condon, E. U.; G. H. Shortley (1935). The Theory of Atomic Spectra. Cambridge University Press. ISBN 0-521-09209-4. (Chapter 16 provides a comprehensive treatment, as of 1935.)
• Zeeman, P. (1897). "On the influence of Magnetism on the Nature of the Light emitted by a Substance". Phil. Mag. 43: 226.
• Zeeman, P. (1897). "Doubles and triplets in the spectrum produced by external magnetic forces". Phil. Mag. 44 (266): 55. doi:10.1080/14786449708621028.
• Zeeman, P. (11 February 1897). "The Effect of Magnetisation on the Nature of Light Emitted by a Substance". Nature. 55 (1424): 347. Bibcode:1897Natur..55..347Z. doi:10.1038/055347a0.

 حديث

• Feynman, Richard P., Leighton, Robert B., Sands, Matthew (1965). The Feynman Lectures on Physics, Vol. 3. Addison-Wesley. ISBN 0-201-02115-3.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Forman, Paul (1970). "Alfred Landé and the anomalous Zeeman Effect, 1919-1921". Historical Studies in the Physical Sciences. 2: 153–261. doi:10.2307/27757307.
• Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. ISBN 0-13-805326-X.
• Liboff, Richard L. (2002). Introductory Quantum Mechanics. Addison-Wesley. ISBN 0-8053-8714-5.
• Sobelman, Igor I. (2006). Theory of Atomic Spectra. Alpha Science. ISBN 1-84265-203-6.
• Foot, C. J. (2005). Atomic Physics. ISBN 0-19-850696-1.