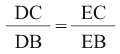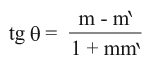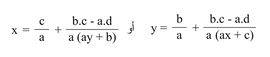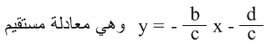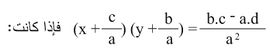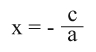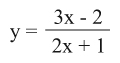المجانسة

Points A, B, C, D and A', B', C', D' are related by a projective transformation.

المجانسة homography أو التقابل المتجانس homographic correspondence هو التقابل بين متحولين جبريين حقيقيين x وy؛ كل منهما من الدرجة الأولى، تربطهما العلاقة axy + bx + cy + d = 0 حيث a, b, c, d ∈ R (a,b,c,d أعداد حقيقية). يمكن أن تكون x وy فاصلتي نقطتين على محور واحد (أو على محورين مختلفين)، أو أمثال توجيه مستقيمين، أو غير ذلك.

ملف:مجانسة1.jpg

الشكل (1)

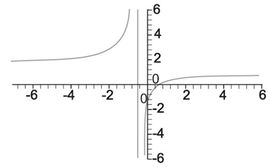
مثال (1): لتكن M(x, y) نقطة ما من منحني الدالة (التابع) (الشكل 1) إحداثياها x وy اللذان تربطهما علاقة المجانسة 2xy - 3x + y + 2 = 0.

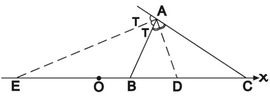
مثال (2): ليكن المثلث ABC (الشكل 2) فيه AD وAE منصفاً زاوية الرأس A (الداخلي والخارجي). يوجد تناسب بين أطوال القطع المستقيمة

فإذا اتخذ BC محوراً، واتخذت نقطة ما منه O (مثلاً) مبدأً للإحداثيات،

الشكل (2)

فإن الفاصلتين x وx`

الشكل (3)

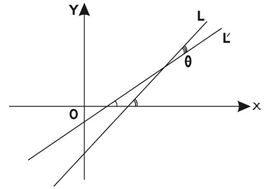
مثال (3): ليكن L وL` مستقيمين متقاطعين في المستوي المنسوب إلى المحورين الإحداثيين OX وOY ميلاهما m وm` والزاوية بينهما θ فإن:

فإذا كانت tg θ = α فإن الميلين m وm` تربطهما علاقة المجانسة:

α m m`+ m`- m + α = 0

خصائص أساسية لعلاقة المجانسة axy + bx + cy + d = 0:

1) في الحالة العامة عندما a ≠ 0 يمكن حساب أحد المتحولين بدلالة الآخر، مثلاً:

2) عندما a = 0 وb, c ≠ 0 يمكن التعبير عن أحد المتحولين كتابع للآخر بعلاقة خطية، مثلاً:

3) a ≠ 0 يجعل العلاقة axy + bx + cy + d = 0 مكافئة للعلاقة (ax + c) (ay + b) = b.c - a.d أو

آ) b.c - a.d ≠ 0 فكل قيمة منتهية

للمتحول y تقابلها قيمة منتهية للمتحول x. أما إذا اقتربت x من القيمة

فإن قيمة y تسعى إلى اللانهاية.

ملف:مجانسةjpg.14

ملف:مجانسةjpg.15

فإن قيمة x تصبح غير مُعرَّفة.

وإذا اقتربت y من القيمة

ملف:مجانسة 16.jpg

فإن قيمة x تسعى إلى اللانهاية. وإذا غدت

فإن قيمة x تصبح غير مُعرَّفة

ب) b.c - a.d = 0 فالعلاقة تصبح:

وتدعى شاذة singular أو معتلة improper، ولا تعين نقاط تقابل متجانس.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 انظر أيضاً

• Epipolar geometry
• W-curve

 المصادر

• الموسوعة العربية

• O. Chum and T. Pajdla and P. Sturm (2005). "The Geometric Error for Homographies". Computer Vision and Image Understanding. 97 (1): 86–102. doi:10.1016/j.cviu.2004.03.004.
• Gunter Ewald (1971) Geometry: An Introduction, page 263, Belmont:Wadsworth Publishing ISBN 0-534-00034-7 .
• Bill Goldman (2005) Transformations in Circle Geometry, course notes from University of Maryland.
• Frank Morley and F.V. Morley (1933) Inversive Geometry, page 38, London: G. Bell and Sons.

 وصلات خارجية

• M. Lourakis' homest is a GPL C/C++ library for robust, non-linear (based on the Levenberg-Marquardt algorithm) homography estimation from matched point pairs. homest can estimate fully projective and affine homographies with a variety of objective functions.
• OpenCV is a complete (open and free) computer vision software library that has many routines related to homography estimation (cvFindHomography) and re-projection (cvPerspectiveTransform). Download and documentation information is on the OpenCV Wiki.
• Computing the plane to plane homography
• How to compute a homography
• MATLAB Functions for Multiple View Geometry Matlab functions for calculating a homography and the fundamental matrix
• Explanation of Homography Estimation by David Kriegman