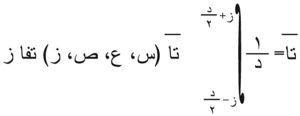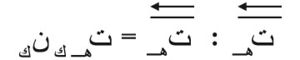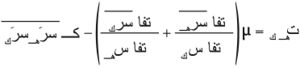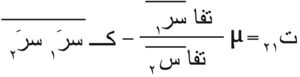اضطراب

Turbulent flow around an obstacle; the flow farther upstream is laminar

Laminar and turbulent water flow over the hull of a submarine

Turbulence in the tip vortex from an airplane wing

الاضطراب turbulence الحركة الاضطرابية هي حركة غير نظامية تنشأ في السائل أو الغاز الذي يجري حول جسم صلب أو داخل أنبوب أو على تماس مع وسط مائعي آخر.

والحركات الاضطرابية هي، من الوجهة العملية، أهم الحركات في ميكانيك الموائع. ويُعدّ الوصول إلى نظرية دقيقة في هذه الحركات، خطوة مهمة في هذا الفرع من الميكانيك، كما يمثل تقدماً كبيراً في حل إحدى مسائل الصراع للحيلولة دون تلوث المائِعَين المهمين للحياة الإنسانية الماء والهواء.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

تاريخ

وقد يكون العالم الألماني هاغِن Hagen هو أول من لاحظ التغير المفاجئ في سلوك حركة سائل يجري في أنبوب أسطواني عندما تتجاوز سرعة الجريان حداً معيناً. ففي حال سرع صغيرة للسائل ظهرت الحركة لهاغِن منتظمة وكان مسار كل جزيئة مستقيماً يوازي محور الأسطوانة، أما سرع جزيئات السائل فإنها تزداد بدءاً من الصفر على جدار الأسطوانة حتى تصل إلى قيمة عظمى على محورها. ويمكن تصور السائل مكوناً من طبقات أسطوانية محورها محور الأسطوانة، وسائل أي طبقة لايختلط بسائل طبقة أخرى. ويقال عن الحركة في مثل هذه الحالة إنها صفحية أو طبقية laminar. وعندما أخذ هاغِن يزيد من السرعة الوسطى للسائل تدريجياً (والسرعة الوسطى عند نقطة من نقاط محور الأسطوانة هي بالتعريف حاصل قسمة حجم السائل الذي يجتاز مقطعاً عمودياً على المحور عند هذه النقطة في واحدة الزمن على مساحة هذا المقطع) لاحظ أن حركة السائل قد أخذت شكلاً فوضوياً عندما تجاوزت السرعة الوسطى حداً معيناً، فمسارات الجزيئات لم تعد مستقيمات، وطبقات السائل أخذت تختلط بعضها ببعض. يقال عن هذه الحركة في هذه الحالة، إنها اضطرابية turbulent. ولإظهار الانتقال من الحركة الصفحية إلى الحركة الاضطرابية على نحو جلي عمد أُسبورْن رينولد (Osborne Reynolds (1842- 1912 عام 1882 إلى تلوين خيط من السائل الذي يجري في الأنبوب، فلاحظ أن هذا الخيط الذي أصابه التلوين يتحرك على نحو مستقيم في الحركة الصفحية من دون أن يختلط مع غيره من السائل. ولكن الأمر لم يستقم على هذه الحال عندما زاد رينولد من السرعة متجاوزاً حداً معيناً، فاللون انتشر داخل الأنبوب، وغدا السائل كله ملوناً، والحركة إذن انقلبت إلى اضطرابية. ويمكن كذلك ملاحظة الجريان الاضطرابي بفتح صنبور من الماء: فعندما تكون السرعة ضعيفة يكون شعاع الماء مستقراً وانزلاقياً، ولكن إذا تجاوزت السرعة حداً معيناً أضحت الحركة غير منتظمة وغير انزلاقية.

Laminar and turbulent flow of cigarette smoke.

والانتقال من الشكل الصفحي إلى الشكل الاضطرابي لايتم بزيادة السرعة فقط، بل يمكن أن يتم أيضاً بتغيير عامل اللزوجة (عن طريق تغيير درجة الحرارة) أو عن طريق تغيير نصف قطر الأنبوب. ولقد لاحظ رينولد أن هذا الانتقال يتم عندما يتجاوز عدد رينولد (ر) الذي يساوي قيمة معينة تدعى عدد رينولد الحرج رح حيث يكون نق: نصف قطر الأنبوب، سر: السرعة الوسطى للسائل، v عامل اللزوجة التحريكية للسائل، وحرف v حرف من الأبجدية اليونانية يقابل n في اللاتينية ويلفظ نو. وهكذا يتبين أن الجريان يكون صفحياً إذا كان ر ‹ رح (وهذا يحصل عندما تكون السرع الوسطى صغيرة، أو تكون الأنابيب ضيقة أو تكون السوائل شديدة اللزوجة)، أما إذا كان ر › رح فالجريان اضطرابي.

وقيمة رح ليست ثابتة بل تتعلق بالشروط التي تتم فيها التجربة. فقد لوحظ مثلاً أن هذه القيمة تزداد كلما جُعل الجدار الداخلي للأنبوب أكثر نعومة، وكلما أُضعف أثر الاضطرابات على السائل (إن مثل هذه الظاهرة تُذكِّر بظاهرة تأخر الغليان في السوائل النقية). ويمكن القول: إنه لا توجد قيمة عظمى لـ رح (أي أنه يمكن زيادة رح بالقدر الذي نشاء بتحسين الشروط)، ولكن هناك قيمة صغرى لـ رح، وحركة السائل تكون صفحية إذا كانت قيمة ر أصغر منها مهما كانت الشروط سيئة. والحركة الاضطرابية لا تحدث فقط في الأنابيب بل يمكن أن تحصل في سائل يجري بين صفيحتين مستويتين متوازيتين أو في سوائل تجري حول أجسام. ومما يميز الحركة الصفحية عن الحركة الاضطرابية هو أن انخفاض الضغط في السائل الذي يجري في أنبوب والناشئ عن الاحتكاك يتناسب طرداً مع السرعة الوسطى للجريان وعكساً مع مربع نصف قطر الأنبوب في حالة الجريان الصفحي، وهو يقترب من أن يكون متناسباً مع مربع السرعة الوسطى طرداً ومع نصف قطر الأنبوب عكساً في حالة الجريان الاضطرابي. وعدم الانتظام في الحركة الاضطرابية يجعل من العسير وصفها بجميع تفاصيلها بدءاً من معطيات مميزة آنية، والدراسة الوحيدة الممكنة، حالياً، تستند على نظريات إحصائية. ولدراسة الحركة الاضطرابية يمكن عدها ناشئة عن تركيب حركتين تدعى إحداهما الحركة الاضطرابية الوسطى والثانية هي حركة شبه دورية.

الحركة الاضطرابية الوسطى

تعرَّف القيمة الوسطى الزمنية تا لعنصر مميِّز كيفي تا لسائل (قد يكون هذا العنصر إحدى مركبات السرعة أو الضغط أو درجة الحرارة) في نقطة ن من الجريان بـ:

يفترض في هذا التعريف وجود زمن د، كبير بالمقارنة مع أدوار التراوحات fluctuationsالاضطرابية، وصغير بالمقارنة مع زمن مميز للحركة الوسطى (الزمن المميز في حالة الجريان في الأنبوب مثلاً هو النسبة بين قطر الأنبوب والسرعة الوسطى للسائل الذي يجري فيه). تتعرف عندئذ الحركة الوسطى بحقل مركبات السرع الوسطى سرھ. فإذا كانت جميع العناصر المميزة الوسطى للسائل في النقطة المفروضة ن ثابتة مهما كانت اللحظة ز، أي إن

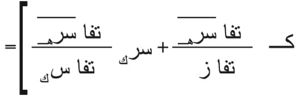
فيقال إن الحركة الاضطرابية مستقرة وسطياً. وأما التراوح تا َ للعنصر المميز المفروض فإنه يعطَى بعلاقة تربط القيمة الآنية لهذا العنصر بالقيمة الوسطى تا= تا + تاَ وبـ تاَ=0 (استناداً إلى التعريف). وتتعرف الحركة الخضِّية agitation بتراوحات مركبات السرع سرھ. ولقد أوضح تسجيل تراوحات السرع وجود طيف تواتر كبير، وذلك بافتراض وجود أعاصير (دوامات) vortices من حجم وشدة متغيرين. ويمكن كتابة المعادلات الموضعية للحركة الوسطى (معادلات رينولد) بالشكل المبسط التالي:

(حيث: ض: الضغط، u عامل اللزوجة، كـ: الكثافة الحجمية)، وحيث تمّ الأخذ بمصطلح الجمع في هذه العلاقات (ينص مصطلح الجمع على مايلي: إذا تكرر دليلٌ مرتين في حد واحد فإن هناك عملية جمع في هذا الدليل تمتد بقدر أبعاد الفضاء الذي تُبحث فيه الظاهرة، فالمعادلة الثانية الأخيرة

ويكون للمقاومة ت الناشئة عن الاحتكاك، في الحركة الوسطى، في موضع ن، عنصرُ السطح عنده ن، المركبات

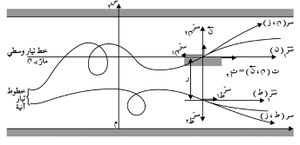
وفي الحالة الخاصة، حالة الجريان بين صفيحتين مستويتين، تكون الحركة الوسطى في اتجاه المحور م س1 (انظر الشكل) ويكون:

وباستثناء الجوار المباشر للجدار تكون مقاومة نيوتن الصفحية

مهملة أمام مقاومة رينولد الاضطرابية التي هي مسؤولة عن تبدد dissipation الطاقة وسط السائل، وبهذا يتضح الدور المهم الذي يؤديه موتر tensor المقاومة الاضطرابية في دراسة الاضطراب. إن معادلات رينولد الموضعية الأربع تشتمل على عشرة مجاهيل وهي الضغط ض، ومركبات السرعة الوسطى سرھ الثلاث، ومركبات موتر المقاومات الاضطرابية وعددها، بسبب تناظر الموتر، ست مركبات. وهكذا يتبين أنه إذا لم تكن هناك فرضيات إضافية فإن هذه المجموعة من المعادلات تبقى غير معينة، ولإزالة عدم التعيين هذا يُلجأ إلى نماذج الاضطراب مثل طول خليط برانتل Prandtl، والعلاقات التجريبية التي تتصل ببنية الجريان الاضطرابي على نحوٍ مماثل لقوانين الحركة المتعلقة بطبيعة السائل.

البنية الداخلية للجريانات الاضطرابية

شدة الاضطراب: إن عدم استقرار الجريان يولد أعاصير (دوامات) تنتشر في الجريان الوسطي ثم تتجزأ بعد ذلك إلى أعاصير أصغر تتبدد طاقتها الميكانيكية إلى حرارة. فالطاقة الحركية الوسطى للسائل مثلاً تتفرق إلى طاقة حركية للحركة الوسطى وإلى طاقة حركية للحركة الخضّية. ولذا فمن الطبيعي إظهار أهمية المزيج الاضطرابي، وذلك بحساب نسبة الطاقة الحركية للخض إلى الطاقة الحركية للحركة الوسطى، ويسمى الجذر التربيعي لهذه النسبة شدة الاضطراب، ويرمز لشدة الاضطراب بـ س وينظر لها على أنها الوسيط الاحداثي الأول للجريان الاضطرابي. وعلى سبيل المثال فإن س ≈ 0.001 في الجو وإن س ≈ -0.1 في السَيْل. ويقال عن الاضطراب إنه متماثل المناحي isotropic إذا كان في كل موضع ن، ويقال عنه إنه متجانس إذا كانت هذه القيمة ثابتة ومستقلة عن النقطة ن.

سلم الاضطراب

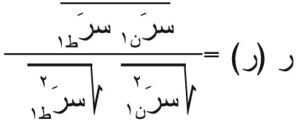
إن التوزيع المكاني لشدة الاضطراب لا يكفي وحده لتعرف الحركة الخضّية تعرفاً متكاملاً، ولابد أيضاً من معرفة التأثير الخاص لجزيئات السائل المختلفة على بعض عناصرها المميزة، وهذا مايسمى بلغة الإحصاء، الارتباط [ر] correlation. وعلى سبيل المثال إذا كان هناك جريان بين صفيحتين متوازيتين واختيرت نقطتان ن، ط في مستو عمودي على الجريان الوسطي تفصلهما مسافة ر، ورُمز لسرعتي هاتين النقطتين بـ سرن، سرط فإن معامل الارتباط ر (ر) بين سرعتي التراوح سرَن1 ،سرَط1 هو:

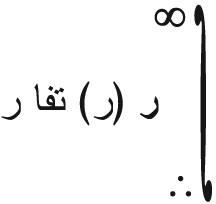
وإن سلم الاضطراب في الاتجاه يعطى تعريفاً بالعبارة:

ويفيد هذا الوسيط الإحصائي الجديد في تحديد القدّ (الحجم) الوسطي للإعصار في الاتجاه المفروض.

أنظر أيضاً

المصادر

الموسوعة العربية

قراءات أخرى

عام

Falkovich, Gregory and Sreenivasan, Katepalli R. Lessons from hydrodynamic turbulence, Physics Today, vol. 59, no. 4, pages 43-49 (April 2006).[1]
U. Frisch. Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press, 1995.[2]
T. Bohr, M.H. Jensen, G. Paladin and A.Vulpiani. Dynamical Systems Approach to Turbulence, Cambridge University Press, 1998.[3]
P.E. Dimotakis [4] High-speed digital-image data acquisition, processing, and Visualization system for turbulent mixing and combustion 2007

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Original scientific research papers

Kolmogorov, Andrey Nikolaevich (1941). "The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers". Proceedings of the USSR Academy of Sciences. 30: 299–303. (بالروسية), translated into English by Kolmogorov, Andrey Nikolaevich (July 8 1991). "The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers". Proceedings of the Royal Society of London, Series A: Mathematical and Physical Sciences. 434 (1980): 9–13. {{cite journal}}: Check date values in: |date= (help)
Kolmogorov, Andrey Nikolaevich (1941). "Dissipation of energy in locally isotropic turbulence". Proceedings of the USSR Academy of Sciences. 32: 16–18. (بالروسية), translated into English by Kolmogorov, Andrey Nikolaevich (July 8 1991). "The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers". Proceedings of the Royal Society of London, Series A: Mathematical and Physical Sciences. 434 (1980): 15–17. {{cite journal}}: Check date values in: |date= (help)

وصلات خارجية