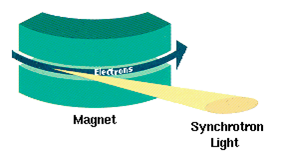
إشعاع سنكروتروني
الإشعاع السنكروتروني (Synchrotron radiation أو إشعاع برمزشترالونگ المغناطيسي magnetobremsstrahlung radiation) هو إشعاع كهرومغناطيسي ينطلق حين تتعرض الجسيمات المشحونة لتسارع قطري، أي حين تتعرض لتسارع عمودي على سرعتها (a ⊥ v). وتُنتَج، على سبيل المثال، في السنكروترونات باستخدام مغناطيسات منحنية، متموجات و/أو متمايلات. إذا كان الجسيم غير نسباوي، فإن الإشعاع يُدعى إشعاع سيكلوتروني. أما إذا كانت الجسيمات نسباوية، فأحياناً يشار إليها بإسم فائق النسباوية، والإشعاع يسمى "إشعاع سنكروتروني".[1] الإشعاع السنكروتروني قد يتحقق اصطناعياً في السنكروترونات أو حلقات التخزين، أو طبيعياً بسبب مرور إلكترونات سريعة خلال مجالات مغناطيسية. الإشعاع الناتج بهذه الطريقة تكون له استقطاب مميز والترددات المتولدة يمكن أن تنتشر على كامل نطاق الطيف الكهرومغناطيسي، ويسمى ذلك الإشعاع أيضاً إشعاع متصل.
من خلال إلكترونيات سريعة الحركة أثناء دورانها في مجال مغناطيسي قوى. والإشعاع السنكروتروني هو سبب الضوضاء والتشويش الراديوي الذي يصدر من خلال معظم المنابع الراديوية في الكون.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
إشعاع سنكروتروني في علم الفلك
تُولد الإشعاعات السنكروترونية في الطبيعة في النجوم و المجرات من الإلكترونات السريعة التي تنتشر بسرعات مقاربة لسرعة الضوء وتقع تحت تأثير مجالات مغناطيسية شديدة فيكون مسارها على هيئة مسارات حلزونية يمكن مراقبتها من الأرض . وهذه تتسم بخاصتين : الخاصة الأولى ، وهو أن طيفها ليس من نوع الطيف العادي الذي ينشأ عن الحرارة ، وهذه تتميز بتوزيع يعرف في الفيزياء بتوزيع الفوتونات الصادرة من الجسم الأسود وتعادل طيف الشمس . والخاصية الثانية ، الاستقطاب.
سدم رياح النباضات
التاريخ
Synchrotron radiation was first observed by technician Floyd Haber, on April 24, 1947, at the 70 MeV electron synchrotron of the General Electric research laboratory in Schenectady, New York.[2] While this was not the first synchrotron built, it was the first with a transparent vacuum tube, allowing the radiation to be directly observed.[3]
As recounted by Herbert Pollock:[4]
On April 24, Langmuir and I were running the machine and as usual were trying to push the electron gun and its associated pulse transformer to the limit. Some intermittent sparking had occurred and we asked the technician to observe with a mirror around the protective concrete wall. He immediately signaled to turn off the synchrotron as "he saw an arc in the tube". The vacuum was still excellent, so Langmuir and I came to the end of the wall and observed. At first we thought it might be due to Cherenkov radiation, but it soon became clearer that we were seeing Ivanenko and Pomeranchuk radiation.[5]
الوصف
A direct consequence of Maxwell's equations is that accelerated charged particles always emit electromagnetic radiation. Synchrotron radiation is the special case of charged particles moving at relativistic speed undergoing acceleration perpendicular to their direction of motion, typically in a magnetic field. In such a field, the force due to the field is always perpendicular to both the direction of motion and to the direction of field, as shown by the Lorentz force law.
The power carried by the radiation is found (in SI units) by the relativistic Larmor formula:[6][7]
- is the vacuum permittivity,
- is the particle charge,
- is the magnitude of the acceleration,
- is the speed of light,
- is the Lorentz factor,
- ,
- is the radius of curvature of the particle trajectory.
The force on the emitting electron is given by the Abraham–Lorentz–Dirac force.
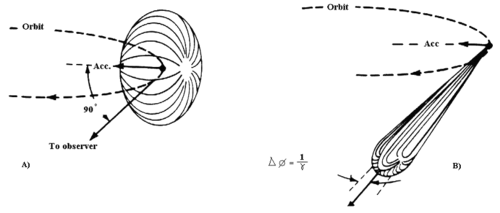
When the radiation is emitted by a particle moving in a plane, the radiation is linearly polarized when observed in that plane, and circularly polarized when observed at a small angle. Considering quantum mechanics, however, this radiation is emitted in discrete packets of photons and has significant effects in accelerators called quantum excitation. For a given acceleration, the average energy of emitted photons is proportional to and the emission rate to .
من المعجلات
Circular accelerators will always produce gyromagnetic radiation as the particles are deflected in the magnetic field. However, the quantity and properties of the radiation are highly dependent on the nature of the acceleration taking place. For example, due to the difference in mass, the factor of in the formula for the emitted power means that electrons radiate energy at approximately 1013 times the rate of protons.[8]
Energy loss from synchrotron radiation in circular accelerators was originally considered a nuisance, as additional energy must be supplied to the beam in order to offset the losses. However, beginning in the 1980s, circular electron accelerators known as light sources have been constructed to deliberately produce intense beams of synchrotron radiation for research.[9]
في الفلك
Synchrotron radiation is also generated by astronomical objects, typically where relativistic electrons spiral (and hence change velocity) through magnetic fields. Two of its characteristics include power-law energy spectra and polarization.[10] It is considered to be one of the most powerful tools in the study of extra-solar magnetic fields wherever relativistic charged particles are present. Most known cosmic radio sources emit synchrotron radiation. It is often used to estimate the strength of large cosmic magnetic fields as well as analyze the contents of the interstellar and intergalactic media.[11]
History of detection
This type of radiation was first detected in a jet emitted by Messier 87 in 1956 by Geoffrey R. Burbidge,[12] who saw it as confirmation of a prediction by Iosif S. Shklovsky in 1953. However, it had been predicted earlier (1950) by Hannes Alfvén and Nicolai Herlofson.[13] Solar flares accelerate particles that emit in this way, as suggested by R. Giovanelli in 1948 and described by J.H. Piddington in 1952.[14]
T. K. Breus noted that questions of priority on the history of astrophysical synchrotron radiation are complicated, writing:
In particular, the Russian physicist V.L. Ginzburg broke his relationships with I.S. Shklovsky and did not speak with him for 18 years. In the West, Thomas Gold and Sir Fred Hoyle were in dispute with H. Alfven and N. Herlofson, while K.O. Kiepenheuer and G. Hutchinson were ignored by them.[مطلوب توضيح][15]

From supermassive black holes
It has been suggested that supermassive black holes produce synchrotron radiation in "jets", generated by the gravitational acceleration of ions in their polar magnetic fields. The nearest such observed jet is from the core of the galaxy Messier 87. This jet is interesting for producing the illusion of superluminal motion as observed from the frame of Earth. This phenomenon is caused because the jets are traveling very near the speed of light and at a very small angle towards the observer. Because at every point of their path the high-velocity jets are emitting light, the light they emit does not approach the observer much more quickly than the jet itself. Light emitted over hundreds of years of travel thus arrives at the observer over a much smaller time period, giving the illusion of faster than light travel, despite the fact that there is actually no violation of special relativity.[16]
Pulsar wind nebulae
A class of astronomical sources where synchrotron emission is important is pulsar wind nebulae, also known as plerions, of which the Crab nebula and its associated pulsar are archetypal. Pulsed emission gamma-ray radiation from the Crab has recently been observed up to ≥25 GeV,[17] probably due to synchrotron emission by electrons trapped in the strong magnetic field around the pulsar. Polarization in the Crab nebula[18] at energies from 0.1 to 1.0 MeV, illustrates this typical property of synchrotron radiation.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Interstellar and intergalactic media
Much of what is known about the magnetic environment of the interstellar medium and intergalactic medium is derived from observations of synchrotron radiation. Cosmic ray electrons moving through the medium interact with relativistic plasma and emit synchrotron radiation which is detected on Earth. The properties of the radiation allow astronomers to make inferences about the magnetic field strength and orientation in these regions. However, accurate calculations of field strength cannot be made without knowing the relativistic electron density.[11]
في المستعرات العظمى
When a star explodes in a supernova, the fastest ejecta move at semi-relativistic speeds approximately 10% the speed of light.[19] This blast wave gyrates electrons in ambient magnetic fields and generates synchrotron emission, revealing the radius of the blast wave at the location of the emission.[20] Synchrotron emission can also reveal the strength of the magnetic field at the front of the shock wave, as well as the circumstellar density it encounters, but strongly depends on the choice of energy partition between the magnetic field, proton kinetic energy, and electron kinetic energy. Radio synchrotron emission has allowed astronomers to shed light on mass loss and stellar winds that occur just prior to stellar death.[21][22]
الصياغة
مجال لينار-ڤيكرت
فلنبدأ بتعبيرات عن مجال لينار-ڤيكرت لشحنة نقطية بكتلة and charge :
where R(t′) = r − r0(t′), R(t′) = |R(t′)|, and n(t′) = R(t′)/R(t′), which is the unit vector between the observation point and the position of the charge at the retarded time, and t′ is the retarded time.
In equation (1), and (2), the first terms for B and E resulting from the particle fall off as the inverse square of the distance from the particle, and this first term is called the generalized Coulomb field or velocity field. These terms represents the particle static field effect, which is a function of the component of its motion that has zero or constant velocity, as seen by a distant observer at r. By contrast, the second terms fall off as the inverse first power of the distance from the source, and these second terms are called the acceleration field or radiation field because they represent components of field due to the charge's acceleration (changing velocity), and they represent E and B which are emitted as electromagnetic radiation from the particle to an observer at r.
If we ignore the velocity field in order to find the power of emitted EM radiation only, the radial component of Poynting's vector resulting from the Liénard–Wiechert fields can be calculated to be
لاحظ أن
- The spatial relationship between β← and قالب:Overset determines the detailed angular power distribution.
- The relativistic effect of transforming from the rest frame of the particle to the observer's frame manifests itself by the presence of the factors (1 − β←⋅n̂) in the denominator of Eq. (3).
- For ultrarelativistic particles the latter effect dominates the whole angular distribution.
The energy radiated into per solid angle during a finite period of acceleration from t′ = T1 to t′ = T2 is
Integrating Eq. (4) over the all solid angles, we get the relativistic generalization of Larmor's formula
However, this also can be derived by relativistic transformation of the 4-acceleration in Larmor's formula.
السرعة العمودية على التسارع (v ⟂ a): الإشعاع السنكروتروني
When the charge is in instantaneous circular motion, its acceleration قالب:Overset is perpendicular to its velocity β←. Choosing a coordinate system such that instantaneously β← is in the z direction and قالب:Overset is in the x direction, with the polar and azimuth angles θ and φ defining the direction of observation, the general formula Eq. (4) reduces to
In the relativistic limit , the angular distribution can be written approximately as
The factors (1 − βcosθ) in the denominators tip the angular distribution forward into a narrow cone like the beam of a headlight pointing ahead of the particle. A plot of the angular distribution (dP/dΩ vs. γθ) shows a sharp peak around θ = 0.
If we neglect any electric force on the particle, the total power radiated (over all solid angle) from Eq. (4) is
where E is the particle's total (kinetic plus rest) energy, B is the magnetic field, and ρ is the radius of curvature of the track in the field. Note that the radiated power is proportional to 1/m4, 1/ρ2, and B2. In some cases the surfaces of vacuum chambers hit by synchrotron radiation have to be cooled because of the high power of the radiation.
باستخدام
where α is the angle between the velocity and the magnetic field and r is the radius of the circular acceleration, the power emitted is:
Thus the power emitted scales as energy to the fourth, and decreases with the square of the radius and the fourth power of particle mass. This radiation is what limits the energy of an electron-positron circular collider. Generally, proton-proton colliders are instead limited by the maximum magnetic field; this is why, for example, the LHC has a center-of-mass energy 70 times higher than the LEP even though the proton mass is 2000 times the electron mass.
تكامل الإشعاع
The energy received by an observer (per unit solid angle at the source) is
Using the Fourier transformation we move to the frequency space
Angular and frequency distribution of the energy received by an observer (consider only the radiation field)
Therefore, if we know the particle's motion, cross products term, and phase factor, we could calculate the radiation integral. However, calculations are generally quite lengthy (even for simple cases as for the radiation emitted by an electron in a bending magnet, they require Airy function or the modified Bessel functions).
مثال 1: المغناطيس المنحني
التكامل
مسار قوس محيط هو
In the limit of small angles we compute
Substituting into the radiation integral and introducing
حيث الدالة K is a modified Bessel function of the second kind.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
توزيع تردد الطاقة المنبعثة
From Eq.(10), we observe that the radiation intensity is negligible for . Critical frequency is defined as the frequency when ξ = 1/2 and θ = 0. So,
and critical angle is defined as the angle for which and is approximately
For frequencies much larger than the critical frequency and angles much larger than the critical angle, the synchrotron radiation emission is negligible.
Integrating on all angles, we get the frequency distribution of the energy radiated.
فإذا عرّفنا
حيث y = ω/ωc. فإن
Note that , if , and , if
The formula for spectral distribution of synchrotron radiation, given above, can be expressed in terms of a rapidly converging integral with no special functions involved[24] (see also modified Bessel functions ) by means of the relation:
انبعاث الإشعاع السنكروتروني كدالة في طاقة الشعاع
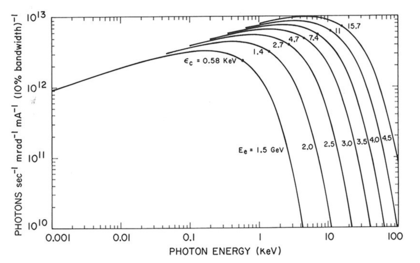
First, define the critical photon energy as
Then, the relationship between radiated power and photon energy is shown in the graph on the right side. The higher the critical energy, the more photons with high energies are generated. Note that, there is no dependence on the energy at longer wavelength.
استقطاب الإشعاع السنكروتروني
In Eq.(10), the first term is the radiation power with polarization in the orbit plane, and the second term is the polarization orthogonal to the orbit plane.
In the orbit plane , the polarization is purely horizontal. Integrating on all frequencies, we get the angular distribution of the energy radiated
Integrating on all the angles, we find that seven times as much energy is radiated with parallel polarization as with perpendicular polarization. The radiation from a relativistically moving charge is very strongly, but not completely, polarized in the plane of motion.
المثال 2: المتموج undulator
حل معادلة الحركة ومعادلة المتموج
يتكون المتموج من مصفوفة دورية من المغناطيسات، بحثي يعطوا مجال مغناطيسي جيبي.
حل معادلة الحركة هو
حيث
و
and the parameter is called the undulator parameter.
Condition for the constructive interference of radiation emitted at different poles is
Expanding and neglecting the terms in the resulting equation, one obtains
For , one finally gets
هذه المعادلة تسمى معادلة المتموج undulator equation.
الإشعاع من المتموج
تكامل الإشعاع هو
Using the periodicity of the trajectory, we can split the radiation integral into a sum over terms, where is the total number of bending magnets of the undulator.
where
, and , , and
The radiation integral in an undulator can be written as
where is the frequency difference to the n-th harmonic. The sum of δ generates a series of sharp peaks in the frequency spectrum harmonics of fundamental wavelength
and Fn depends on the angles of observations and K
On the axis (θ = 0, φ = 0), the radiation integral becomes
و
where
لاحظ أن only odd harmonics are radiated on-axis, and as K increases higher harmonic becomes stronger.
المصادر
- مؤمن, عبد الأمير (2006). قاموس دار العلم الفلكي. بيروت، لبنان: دار العلم للملايين.
{{cite book}}: Cite has empty unknown parameter:|طبعة أولى coauthors=(help)
انظر أيضا
- منبع راديوي
- إشعاع كهرومغناطيسي
- إشعاع
- Synchrotron for this type of particle accelerator
- Synchrotron light source for laboratory generation and applications of synchrotron radiation
- Cyclotron Radiation
- Relativistic beaming
- Radiation reaction
- Sokolov–Ternov effect
ملاحظات
- ^ Yale Astronomy http://www.astro.yale.edu/vdbosch/astro320_summary27.pdf
- ^ Elder, F. R.; Gurewitsch, A. M.; Langmuir, R. V.; Pollock, H. C. (1 June 1947). "Radiation from Electrons in a Synchrotron". Physical Review. American Physical Society. 71 (11): 829–830. Bibcode:1947PhRv...71..829E. doi:10.1103/physrev.71.829.5. ISSN 0031-899X.
- ^ Mitchell, Edward; Kuhn, Peter; Garman, Elspeth (May 1999). "Demystifying the synchrotron trip: a first time user's guide". Structure. 7 (5): R111–R121. doi:10.1016/s0969-2126(99)80063-x. PMID 10378266.
- ^ Pollock, Herbert C. (March 1983). "The discovery of synchrotron radiation". American Journal of Physics. 51 (3): 278–280. Bibcode:1983AmJPh..51..278P. doi:10.1119/1.13289.
- ^ Iwanenko, D.; Pomeranchuk, I. (1 June 1944). "On the Maximal Energy Attainable in a Betatron". Physical Review. American Physical Society. 65 (11–12): 343. Bibcode:1944PhRv...65..343I. doi:10.1103/physrev.65.343. ISSN 0031-899X.
- ^ Wilson, E. J. N. (2001). An introduction to particle accelerators. Oxford: Oxford University Press. pp. 221–223. ISBN 0-19-850829-8.
- ^ Fitzpatrick, Richard. Classical Electromagnetism (PDF) (in الإنجليزية). p. 299.
- ^ Conte, Mario; MacKay, William (2008). An introduction to the physics of particle accelerators (2nd ed.). Hackensack, N.J.: World Scientific. p. 166. ISBN 978-981-277-960-1.
- ^ "History: Of X-rays and synchrotrons". lightsources.org. 21 September 2017. Retrieved 13 December 2021.
- ^ Vladimir A. Bordovitsyn, "Synchrotron Radiation in Astrophysics" (1999) Synchrotron Radiation Theory and Its Development, ISBN 981-02-3156-3
- ^ أ ب Klein, Ulrich (2014). Galactic and intergalactic magnetic fields. Cham, Switzerland & New York: Springer. ISBN 978-3-319-08942-3. OCLC 894893367.
- ^ Burbidge, G. R. (1956). "On Synchrotron Radiation from Messier 87". The Astrophysical Journal. IOP Publishing. 124: 416. Bibcode:1956ApJ...124..416B. doi:10.1086/146237. ISSN 0004-637X.
- ^ Alfvén, H.; Herlofson, N. (1 June 1950). "Cosmic Radiation and Radio Stars". Physical Review. APS. 78 (5): 616. Bibcode:1950PhRv...78..616A. doi:10.1103/physrev.78.616. ISSN 0031-899X.
- ^ Piddington, J. H. (1953). "Thermal Theories of the High-Intensity Components of Solar Radio-Frequency Radiation". Proceedings of the Physical Society. Section B. IOP Publishing. 66 (2): 97–104. Bibcode:1953PPSB...66...97P. doi:10.1088/0370-1301/66/2/305. ISSN 0370-1301.
- ^ Breus, T. K., "Istoriya prioritetov sinkhrotronnoj kontseptsii v astronomii %t (Historical problems of the priority questions of the synchrotron concept in astrophysics)" (2001) in Istoriko-Astronomicheskie Issledovaniya, Vyp. 26, pp. 88–97, 262 (2001)
- ^ Chase, Scott I. "Apparent Superluminal Velocity of Galaxies". Retrieved 22 August 2012.
- ^ Aliu, E.; Anderhub, H.; Antonelli, L. A.; Antoranz, P.; Backes, M.; et al. (21 November 2008). "Observation of Pulsed γ-Rays Above 25 GeV from the Crab Pulsar with MAGIC". Science. 322 (5905): 1221–1224. arXiv:0809.2998. Bibcode:2008Sci...322.1221A. doi:10.1126/science.1164718. ISSN 0036-8075. PMID 18927358. S2CID 5387958.
- ^ Dean, A. J.; Clark, D. J.; Stephen, J. B.; McBride, V. A.; Bassani, L.; et al. (29 August 2008). "Polarized Gamma-Ray Emission from the Crab". Science. American Association for the Advancement of Science (AAAS). 321 (5893): 1183–1185. Bibcode:2008Sci...321.1183D. doi:10.1126/science.1149056. ISSN 0036-8075. PMID 18755970. S2CID 206509342.
- ^ Soderberg, A.; Chevalier, R. A.; Kulkarni, S. R.; Frail, D. A. (November 2006). "The Radio and X-Ray Luminous SN 2003bg and the Circumstellar Density Variations around Radio Supernovae". The Astrophysical Journal. 651 (2): 1005–1018. arXiv:astro-ph/0512413. Bibcode:2006ApJ...651.1005S. doi:10.1086/507571.
- ^ Chevalier, R. A. (May 1998). "Synchrotron Self-Absorption in Radio Supernovae". The Astrophysical Journal. 499 (2): 810–819. Bibcode:1998ApJ...499..810C. doi:10.1086/305676.
- ^ Margutti, Raffaella; et al. (February 2017). "Ejection of the Massive Hydrogen-rich Envelope Timed with the Collapse of the Stripped SN 2014C". The Astrophysical Journal. 835 (2): 140. arXiv:1601.06806. Bibcode:2017ApJ...835..140M. doi:10.3847/1538-4357/835/2/140. hdl:10150/624387. PMC 5495200. PMID 28684881.
- ^ DeMarchi, Lindsay; et al. (October 2022). "Radio Analysis of SN2004C Reveals an Unusual CSM Density Profile as a Harbinger of Core Collapse". The Astrophysical Journal. 938 (1): 84. arXiv:2203.07388. Bibcode:2022ApJ...938...84D. doi:10.3847/1538-4357/ac8c26.
- ^ Jackson, John David (1999). Classical Electrodynamics (3rd ed.). Chichester: Wiley. p. 680. ISBN 978-0-471-30932-1.
- ^ M.Kh.Khokonov. Cascade Processes of Energy Loss by Emission of Hard Photons // JETP, V.99, No.4, pp. 690-707 \ (2004).
وصلات خارجية
- Cosmic Magnetobremsstrahlung (synchrotron Radiation), by Ginzburg, V. L., Syrovatskii, S. I., ARAA, 1965
- Developments in the Theory of Synchrotron Radiation and its Reabsorption, by Ginzburg, V. L., Syrovatskii, S. I., ARAA, 1969
- Lightsources.org
- X-Ray Data Booklet















![{\displaystyle {\begin{aligned}\mathbf {B} (\mathbf {r} ,t)&=-{\frac {\mu _{0}q}{4\pi }}\left[{\frac {c\,{\hat {\mathbf {n} }}\times {\vec {\beta }}}{\gamma ^{2}R^{2}\,(1-{\vec {\beta }}\mathbf {\cdot } {\hat {\mathbf {n} }})^{3}}}+{\frac {{\hat {\mathbf {n} }}\times [\,{\dot {\vec {\beta }}}+{\hat {\mathbf {n} }}\times ({\vec {\beta }}\times {\dot {\vec {\beta }}})]}{R\,(1-{\vec {\beta }}\mathbf {\cdot } {\hat {\mathbf {n} }})^{3}}}\right]_{\mathrm {retarded} },\qquad &(1)\\\mathbf {E} (\mathbf {r} ,t)&={\frac {q}{4\pi \varepsilon _{0}}}\left[{\frac {{\hat {\mathbf {n} }}-{\vec {\beta }}}{\gamma ^{2}R^{2}\,(1-{\vec {\beta }}\mathbf {\cdot } {\hat {\mathbf {n} }})^{3}}}+{\frac {{\hat {\mathbf {n} }}\times [({\hat {\mathbf {n} }}-{\vec {\beta }})\times {\dot {\vec {\beta }}}\,]}{c\,R\,(1-{\vec {\beta }}\mathbf {\cdot } {\hat {\mathbf {n} }})^{3}}}\right]_{\mathrm {retarded} },\qquad &(2)\end{aligned}}}](https://www.marefa.org/api/rest_v1/media/math/render/svg/90d5c533eb6d171a339f099c63e6d1af95876ca1)
![{\displaystyle [\mathbf {S\cdot } {\hat {\mathbf {n} }}]={\frac {q^{2}}{16\pi ^{2}\varepsilon _{0}c}}\left\{{\frac {1}{R^{2}}}\left|{\frac {{\hat {\mathbf {n} }}\times [({\hat {\mathbf {n} }}-{\vec {\beta }})\times {\dot {\vec {\beta }}}]}{(1-{\vec {\beta }}\mathbf {\cdot } {\hat {\mathbf {n} }})^{3}}}\right|^{2}\right\}_{\text{retarded}}.\qquad \qquad (3)}](https://www.marefa.org/api/rest_v1/media/math/render/svg/f9f2b79c35184ff494c80d6bd3561dc441d48604)
![{\displaystyle {\begin{aligned}{\frac {\mathrm {d} P}{\mathrm {d} {\mathit {\Omega }}}}&=R(t')^{2}\,[\mathbf {S} (t')\mathbf {\cdot } {\hat {\mathbf {n} }}(t')]\,{\frac {\mathrm {d} t}{\mathrm {d} t'}}=R(t')^{2}\,\mathbf {S} (t')\mathbf {\cdot } {\hat {\mathbf {n} }}(t')\,[1-{\vec {\beta }}(t')\mathbf {\cdot } {\hat {\mathbf {n} }}(t')]\\&={\frac {q^{2}}{16\pi ^{2}\varepsilon _{0}c}}\,{\frac {|{\hat {\mathbf {n} }}(t')\times \{[{\hat {\mathbf {n} }}(t')-{\vec {\beta }}(t')]\times {\dot {\vec {\beta }}}(t')\}|^{2}}{[1-{\vec {\beta }}(t')\mathbf {\cdot } {\vec {\mathbf {n} }}(t')]^{5}}}.\qquad \qquad (4)\end{aligned}}}](https://www.marefa.org/api/rest_v1/media/math/render/svg/3e7a67ef7a47cf6ad1c46605edb2f5f1d22e4c5e)
![{\displaystyle P={\frac {q^{2}}{6\pi \varepsilon _{0}c}}\gamma ^{6}\left[\left|{\dot {\vec {\beta }}}\right|^{2}-\left|{\vec {\beta }}\times {\dot {\vec {\beta }}}\right|^{2}\right].\qquad (5)}](https://www.marefa.org/api/rest_v1/media/math/render/svg/b24422e3c3923fcb308a20ddc65a0a95a367d28b)
![{\displaystyle {\frac {\mathrm {d} P}{\mathrm {d} {\mathit {\Omega }}}}={\frac {q^{2}}{16\pi ^{2}\epsilon _{0}c}}{\frac {|{\dot {\vec {\beta }}}|^{2}}{(1-\beta \cos \theta )^{3}}}\left[1-{\frac {\sin ^{2}\theta \cos ^{2}\phi }{\gamma ^{2}(1-\beta \cos \theta )^{2}}}\right].\qquad (6)}](https://www.marefa.org/api/rest_v1/media/math/render/svg/f8c8b45efe4509cdbcc6ab6a94e85c3fcdceba77)

![{\displaystyle {\frac {\mathrm {d} P}{\mathrm {d} {\mathit {\Omega }}}}\simeq {\frac {2}{\pi }}{\frac {q^{2}}{c^{3}}}\gamma ^{6}{\frac {|{\dot {\mathbf {v} }}|^{2}}{(1+\gamma ^{2}\theta ^{2})^{3}}}\left[1-{\frac {4\gamma ^{2}\theta ^{2}\cos ^{2}\phi }{(1+\gamma ^{2}\theta ^{2})^{2}}}\right].\qquad \qquad (7)}](https://www.marefa.org/api/rest_v1/media/math/render/svg/0c3edcff9a371724a3913a7c074caaf5fd3fe897)





![{\displaystyle {\frac {d^{3}W}{d\Omega d\omega }}=2c\varepsilon _{0}R^{2}\left|{\vec {E}}(\omega )\right|^{2}={\frac {q^{2}}{4\pi \varepsilon _{0}4\pi ^{2}c}}\left|\int _{-\infty }^{\infty }{\frac {{\hat {n}}\times \left[\left({\hat {n}}-{\vec {\beta }}\right)\times {\dot {\vec {\beta }}}\right]}{\left(1-{\hat {n}}\cdot {\vec {\beta }}\right)^{2}}}e^{i\omega (t-{\hat {n}}\cdot {\vec {r}}(t)/c)}dt\right|^{2}.\qquad (9)}](https://www.marefa.org/api/rest_v1/media/math/render/svg/b66f6e1f938090098d769261e13048d7ca3b6025)


![{\displaystyle {\hat {n}}\times \left({\hat {n}}\times {\vec {\beta }}\right)=\beta \left[-{\vec {\varepsilon }}_{\parallel }\sin \left({\frac {\beta ct}{\rho }}\right)+{\vec {\varepsilon }}_{\perp }\cos \left({\frac {\beta ct}{\rho }}\right)\sin \theta \right]}](https://www.marefa.org/api/rest_v1/media/math/render/svg/3697c27de9faf5e34aa018a84fdc100b0e20bc3a)
![{\displaystyle \omega \left(t-{\frac {{\hat {n}}\cdot {\vec {r}}(t)}{c}}\right)=\omega \left[t-{\frac {\rho }{c}}\sin \left({\frac {\beta ct}{\rho }}\right)\cos \theta \right]}](https://www.marefa.org/api/rest_v1/media/math/render/svg/501ef90445477e3338d71afa51ab7bdd1c334d6d)

![{\displaystyle {\frac {d^{3}W}{d\Omega d\omega }}={\frac {3q^{2}}{16\pi ^{3}\varepsilon _{0}c}}\left({\frac {2\omega \rho }{3c\gamma ^{2}}}\right)^{2}\left(1+\gamma ^{2}\theta ^{2}\right)^{2}\left[K_{2/3}^{2}(\xi )+{\frac {\gamma ^{2}\theta ^{2}}{1+\gamma ^{2}\theta ^{2}}}K_{1/3}^{2}(\xi )\right]\qquad (10),}](https://www.marefa.org/api/rest_v1/media/math/render/svg/eec2f418d41ecf3dadc72fc219072ffc8e41102b)














![{\displaystyle \int _{\xi }^{\infty }K_{5/3}(x)dx={\frac {1}{\sqrt {3}}}\,\int _{0}^{\infty }\,{\frac {9+36x^{2}+16x^{4}}{(3+4x^{2}){\sqrt {1+x^{2}/3}}}}\exp \left[-\xi \left(1+{\frac {4x^{2}}{3}}\right){\sqrt {1+{\frac {x^{2}}{3}}}}\right]\ dx}](https://www.marefa.org/api/rest_v1/media/math/render/svg/ef2cee0b1d4767df120a2da5c695ee0103735860)




![{\displaystyle {\frac {d^{2}W}{d\Omega }}=\int _{0}^{\infty }{\frac {d^{3}W}{d\omega d\Omega }}d\omega ={\frac {7q^{2}\gamma ^{5}}{64\pi \varepsilon _{0}\rho }}{\frac {1}{(1+\gamma ^{2}\theta ^{2})^{5/2}}}\left[1+{\frac {5}{7}}{\frac {\gamma ^{2}\theta ^{2}}{1+\gamma ^{2}\theta ^{2}}}\right].\qquad (12)}](https://www.marefa.org/api/rest_v1/media/math/render/svg/aca2682bcabc7abedfe0676d97f3b7411a71d69e)













![{\displaystyle {\frac {d^{3}W}{d\Omega d\omega }}={\frac {q^{2}}{4\pi \varepsilon _{0}4\pi ^{2}c}}\left|\int _{-\infty }^{\infty }{\frac {{\hat {n}}\times \left[\left({\hat {n}}-{\vec {\beta }}\right)\times {\dot {\vec {\beta }}}\right]}{\left(1-{\hat {n}}\cdot {\vec {\beta }}\right)^{2}}}e^{i\omega (t-{\hat {n}}\cdot {\vec {r}}(t)/c)}dt\right|^{2}.}](https://www.marefa.org/api/rest_v1/media/math/render/svg/799e945d121a99aee45d3c37578f64a38428466d)















![{\displaystyle F_{n}(K,0,0)={\frac {n^{2}K^{2}}{1+K^{2}/2}}\left[J_{\frac {n+1}{2}}(Z)-J_{\frac {n-1}{2}}(Z)\right]^{2},}](https://www.marefa.org/api/rest_v1/media/math/render/svg/c44b94205029811a5970b343c78455f8acf073cf)
