أحجية المربع المفقود
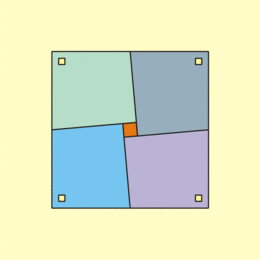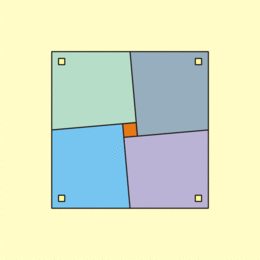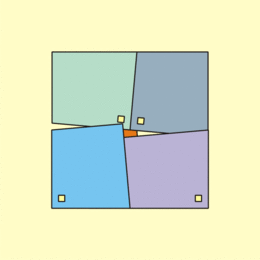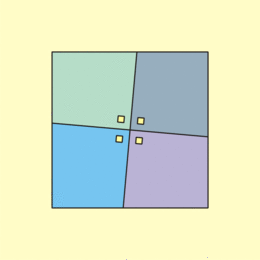
أحجية المربع المفقود هي خدعة بصرية تستعمل في مادة الهندسة]] الرياضية لمساعدة الطلاب في التفكير بالأشكال الهندسية وحساب مساحتها، بالإضافة إلى مساعدتهم في التفكير بتطابق وتشابه المثلثات ومدى تأثير استقامة الخطوط على مساحة أي شكل هندسي مرسوم.
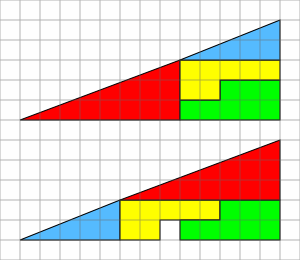
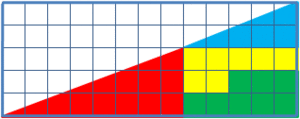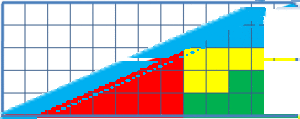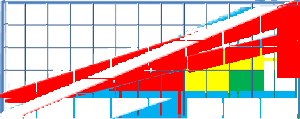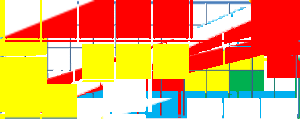
تصوّر الأحجية ترتيبان من الأشكال كل منهما يظهر على شكل مثلث قائم الزاوية، وتبدو أطوال أضلاع كل منهما على أنها 13*5 سم.
مع أن المثلثين يبدوان متطابقان بالحجم عند النظرة الأولى، و ذا الأشكال التي يتألف منها المثلثان، تنقص مساحة مربع واحد من المثلث الأسفل عند ترتيب القطع بشكل مختلف عما كانت عليه. وتبلغ مساحة القطعة الناقصة 1 سم مربع، أي مربع صغير واحد.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
الحل
عند حساب المساحة الإجمالية للأشكال الموجودة مفترقة بواسطة جمع مساحات الأشكال، نحصل على مجموع قيمته 32 سم مربع. أما عند حسابنا للمثلث الصحيح كاملا نحصل على مساحة إجمالية قدرها 32.5 سم مربع (13 سم * 5 سم * 1/2)
فيما تبلغ مساحة المثلث الأول 32 سم مربع، نجد أن مساحة المثلث الأسفل هي 33 سم مربع. اختلاف المساحات هذا ينتج عن عدم تطابق زاويتي المثلثين الأحمر والأزرق (غير متشابهان هندسيا). وبهذا يحتوي كلا "المثلثان" على إنحناء بسيط في امتداد الخط الأحمر إلى المثلث الأزرق.
نستنتج من هذا إذا، أن الضلع الفوقي ليس خطا مستقيما. يمكن التعرف على عدم الإستقامة هذه عند نقطة إلتقاء الأحمر بالإزرق.
كخلاصة، يمكننا القول أن حل الأحجية يكمن في أن كلا المثلثين ليسا بمثلثين، بل هما في الحقيقة مقعّر ومحدّب على التوالي، مع فرق بالمساحة تبلغ قيمته 1 سم مربع، هي تماما مساحة المربع المفقود.