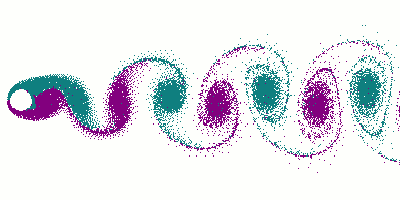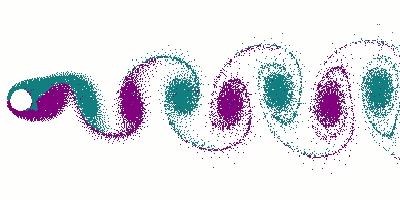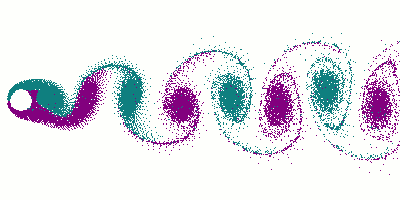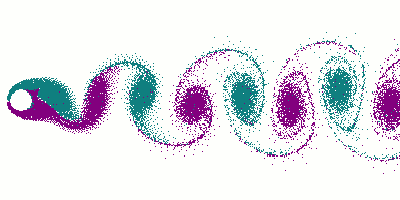شارع دوامات كارمان
في ديناميكا الموائع، شارع دوامات كارمان Kármán vortex street (أو von Kármán vortex sheet)، هو نموذج متكرر من الدوامات الحلزونية التي يسببها انفصال تدفق الموائع حول الأجسام. سميت على اسم المهندس وديناميكي الموائع تيودور فون كارمان،[1] ويكون مسئول عن ظواهر مثل "إنفراد" خطوط الهاتف أو الطاقة المعلقة، واهتزاز هوائي السيارة عند سرعات معينة.
تحليل
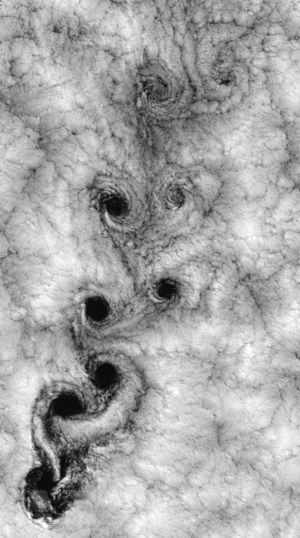
ظاهرة الدوامات وشوارع الدوامات هي ظاهرة تحدث كثيراً، ولكن تصعب مشاهدتها أحياناً. هذا لصعوبة رؤية الرياح وجريان الهواء. الأمر نفسه بالنسبة إلى دوامات الماء يصعب رؤياها بسبب شفافية الماء. ومع ذلك فيمكن بالتمعن رؤي دوامات في حوض مثلا عندما يكون الماء ساكنا ونقطعه بأحد أصابعنا. عندئذ يمكننا مشاهدة "شارع دوامات".
وإذا استبدلنا الماء بسائل ذو لزوجة عالية مثل مخلوط ماء وگلسرين، مع إضافة لون من ألوان الأطعمة، مثل شراب الكرز أو الفرولة، عندئذ نستطيع رؤية أوتار وخيوط ملونة اللون تدور في اتجاه دوران الدوامات.
يمكن حدوث شوراع دوامات كارمان مثلاً خلف جزيرة عالية أو عدة دزر عالية في البحر، ونجدها تعلو عن سطح الماء. وتظهر تلك الدوامات أثناء التصوير من الجو أو من قمر صناعي في هيئة تشكيلات صخمة من السحب.
في الأرصاد الجوية
رصد جبال وجزر تتشهر بتسببها في حدوث شارع دوامات كارمان
- جزيرة گوادالوپه.[2]
- بركان هالسان، جزيرة جيجو، كوريا الجنوبية.[3]
- جزيرة ياكشويما، اليابان.[4]
- جزيرة سكورو، جزيرة بركانية صغيرة ضمن جزر رڤيلاگيگدو، تابعة للمكسيك.[5]
- جميع جزر الكناري.[6]
- جزيرة ماديرا.[7]
- معظم جزر الرأس الأخضر.[8]
- بركان بيرنبرگ، جزيرة يان ماين.[9][10]
- جزيرة هرالد، روسيا.[11]
- جزيرة سانت هلينا.[12]
- جزيرة بروتونا، روسيا.[13]
- جزر چيورنه برايتا، روسيا.[13]
- بركان زاڤودوڤسكي، المحيط الأطلسي الجنوبي.
- تريستان دا كونيا، المحيط الأطلسي الجنوبي.[14]
- جزر ساندوتش الجنوبية.[15]
- الجزر الإليوسية، آلاسكا.[16]
- جزيرة هيرد، جنوب المحيط الهندي.[17]
- جزر گالاپگوس.[18]
- جزر خون فرنانديز، تشيلي.[19]
- جزيرة ريشيري، اليابان.[20]
- جزر كروزت، جنوب المحيط الهندي.[21]
- جزر كوريل.[22]
المشكلات الهندسية
تردد الانفصال
يمكن الحصول على "تردد انفصال" دوامة (انفصال عن العائق) باستخدام رقم ستروهال . تنطبق المعادلة:
- ,
حيث:
- سرعة جريان الوسط، وليكن الماء مثلا،
- و مقاييس الجسم العائق.
يعتمد عدد ستروهال على شكل العائق وعلى رقم رينولد، وهو عدد خاص بالموائع. وبافتراض أن العائق شكله اسطواني فإن عدد رينولد الخاص به بين 0,18-0,22. وسنختار في مثالنا هنا . والبعد الهام بالنسبة لتكون الدوامات هو قطر الأسطوانة حيث تكون الأسطوانة قائمة عموديا في الماء. وبناء على ذلك ينتج هوائي سيارة ذو قطر يبلغ 4 مليمتر ويكون منصوبا على سقف سيارة تسير بسرعة 25 متر في الثانية (90 كم/س)، تنتج صوتا (موسيقى) عاليا واضحا بالتردد:
- .
ومثال آخر:
وهو تصفير خطوط الضغط العالي عند مرور الريح عليها.
ونطرا لكون العلاقة بين "تردد الانفصال" وسرعة جريان المائع هي علاقة خطية (أي تتناسب طرديا مع سرعة جريان المائع)، فيستخدم " مقياس جريان المائع" لتعيين لزوجة المواد ذات لزوجة منخفضة.
التاريخ
بالرغم من تسميته على اسم تيودور فون كارمان،[23][24] إلا أنه اعترف[25] بأن شارع الدوامة سبق دراستها مبكراً بواسطة مالوك[26] وبنار.[27]
انظر أيضاً
- إدي (ديناميكا الموائع)
- Kelvin–Helmholtz instability
- Vortex shedding
- Vortex-induced vibration
- تأثير كواندا
المصادر
- ^ Theodore von Kármán, Aerodynamics. McGraw-Hill (1963): ISBN 978-0-07-067602-2. Dover (1994): ISBN 978-0-486-43485-8.
- ^ "Atmospheric Vortices near Guadalupe Island : Image of the Day". Earthobservatory.nasa.gov. Retrieved 2013-12-20.
- ^ "Miscellaneous". Hko.gov.hk. Retrieved 2013-12-20.
- ^ "Seen from Space - Striped Clouds Crossing over the Sea of Japan". EORC. Retrieved 2013-12-20.
- ^ "Swirls of Lace : Image of the Day". Earthobservatory.nasa.gov. Retrieved 2013-12-20.
- ^ "Rapid Response - LANCE - Terra/MODIS 2010/226 14:55 UTC". Rapidfire.sci.gsfc.nasa.gov. Retrieved 2013-12-20.
- ^ "NASA Visible Earth: Vortex street near Madeira Island". Visibleearth.nasa.gov. Retrieved 2013-12-20.
- ^ [1]
- ^ "A Vortex Street in the Arctic : Image of the Day". Earthobservatory.nasa.gov. Retrieved 2013-12-20.
- ^ http://earthobservatory.nasa.gov/NaturalHazards/view.php?id=77654
- ^ "Wrangel Island, Russia : Image of the Day". Earthobservatory.nasa.gov. Retrieved 2013-12-20.
- ^ "Cloud Vortices off St. Helena : Image of the Day". Earthobservatory.nasa.gov. Retrieved 2013-12-20.
- ^ أ ب "Von Karman Vortices over Broutona : Image of the Day". Earthobservatory.nasa.gov. Retrieved 2013-12-20.
- ^ http://rapidfire.sci.gsfc.nasa.gov/cgi-bin/imagery/single.cgi
- ^ "Rapid Response - LANCE - Terra/MODIS 2012/118 16:20 UTC". Rapidfire.sci.gsfc.nasa.gov. Retrieved 2013-12-20.
- ^ "Rapid Response - LANCE - Terra/MODIS 2012/108 22:40 UTC". Rapidfire.sci.gsfc.nasa.gov. Retrieved 2013-12-20.
- ^ "Rapid Response - LANCE - Terra/MODIS 2011/262 04:30 UTC". Rapidfire.sci.gsfc.nasa.gov. Retrieved 2013-12-20.
- ^ "Rapid Response - LANCE - Terra/MODIS 2010/251 16:35 UTC". Rapidfire.sci.gsfc.nasa.gov. Retrieved 2013-12-20.
- ^ "Rapid Response - LANCE - Terra/MODIS 2010/020 19:20 UTC". Rapidfire.sci.gsfc.nasa.gov. Retrieved 2013-12-20.
- ^ Čeština. "Rishiri Island - Wikipedia, the free encyclopedia". En.wikipedia.org. Retrieved 2013-12-20.
- ^ "NASA Visible Earth: Cloud vortices off the Crozet Islands, south Indian Ocean". Visibleearth.nasa.gov. Retrieved 2013-12-20.
- ^ "Von Karman vortices. Coloured composite satellite image of clouds forming von Karman vortices, an effect that occurs when an object disturbs the flow of a fluid, leading to the creation of a chain of spiral eddies (a vortex street). In this case, the objects causing vortex streets to form are islands in the Kuril Islands chain between Russia and Japan. The effect occurs at all scales and it is imp - Stock Photos". Masterfile.com. Retrieved 2013-12-20.
- ^ T. von Kármán: Nachr. Ges. Wissenschaft. Göttingen Math. Phys. Klasse pp. 509–517 (1911) and pp. 547–556 (1912).
- ^ T. von Kármán: and H. Rubach, 1912: Phys. Z.", vol. 13, pp. 49–59.
- ^ T. Kármán, 1954. Aerodynamics: Selected Topics in the Light of Their Historical Development (Cornell University Press, Ithaca), pp. 68–69.
- ^ A. Mallock, 1907: On the resistance of air. Proc. Royal Soc., A79, pp. 262–265.
- ^ H. Bénard, 1908: Comptes rendus de l'Académie des Sciences (Paris), vol. 147, pp. 839–842, 970–972.
وصلات خارجية
- Encyclopedia of Mathematics article on von Karman vortex shedding
- Kármán vortex street formula calculator
- 3D animation of the Vortex Flow Measuring Principle
- Vortex streets and Strouhal instability
- How Insects Fly (which can produce von Kármán vortices)
- YouTube — Flow visualisation of the vortex shedding mechanism on circular cylinder using hydrogen bubbles illuminated by a laser sheet in a water channel
- Various Views of von Karman Vortices, NASA page