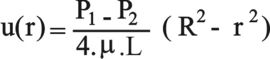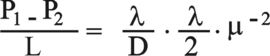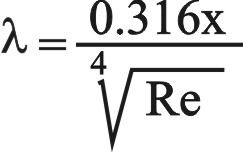طبقة حدية
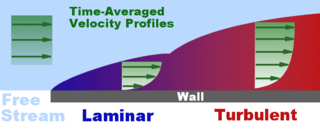
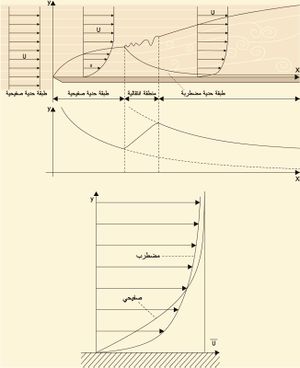
تعتمد نظرية الطبقة الحدية boundary layer على تقسيم الجريان حول جسم ما إلى منطقتين؛ منطقة ملاصقة للجسم تسمى الطبقة الحدِّية، وهي تتميز بتغير كبير في توزع سرعة السائل وبظهور كبير لأثر لزوجته، إذ تنعدم هذه السرعة عند جدار الجسم بسبب كون السائل لزجاً وتزداد بشكل كبير في الطبقة الحدية إلى أن يصبح توزع السرع ثابتاً خارجها، وعندئذ يجري الحديث عن منطقة الجريان المثالي. يوضح الشكل (1) توزع سُرَع الجريان على صفيحة مستوية، إذ يكون الجريان قبل الصفيحة جرياناً منتظماً سرعته U، وعند ملامسة جزيئات السائل لجدار الصفيحة تخضع للكبح نتيجة الاحتكاك ولزوجة السائل، وتنعدم سرعتها عند الجدار. تتزايد سرعة الجزيئات في الطبقة الحدية مع الابتعاد عن الجدار إلى أن تصل إلى منطقة تكون فيها سرعة السائل ثابتة.
أول من طرح فكرة تقسيم الجريان حول الجسم هوالعالم الألماني براندل Prandtl عام 1904، إلا أن البروفسور الألماني شليشتينغ Schlichting هوالذي وضع الأساس النظري والرياضي لنظرية الطبقة الحدية عام 1955، والتي شكَّلت المنطلق لجميع الدراسات الحديثة في مجال ميكانيك السوائل fluid mechanics وديناميك الهواء aerodynamics.
إجهاد الاحتكاك t0 المؤثر في جسم يتعرض للجريان
يكتسب السائل في السوائل الحقيقية (اللزجة) سرعة الجدار الملامس له. أي إن سرعة السائل تكون معدومة على سطح الجدار ثم تتزايد بشكل كبير داخل الطبقة الحدية المحيطة بالجسم إلى أن تأخذ قيمتها النهائية والثابتة خارج الطبقة الحدية. وتعطى قيمة إجهاد الاحتكاك أواللزوجة حسب قانون نيوتن للسوائل اللزجة
الطبقة الحدية الصفيحية والطبقة الحدية المضطربة
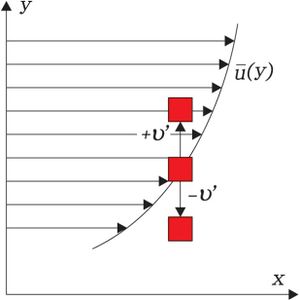
تتحرك جزيئات السائل في بداية الجريان داخل الطبقة الحدية بشكل صفيحي، وبالتالي تتعرض إلى تغير في قيمة السرعة المؤثرة على الجزيئة بسبب توزع السرع في الطبقة الحدية, مما يؤدي إلى ظهور اضطرابات عرضية واهتزازات يتزايد مطالها مع تقدم الجريان كما يظهر في الشكل (1) كذلك, عندئذ يقال إن الجريان في الطبقة الحدية تحوَّل من جريان صفيحي laminar إلى جريان مضطرب turbulent، ويؤدي هذا الاضطراب إلى تبادل في طاقة الجزيئات، وبالتالي إلى توزع سرع أكثر انتظاماً داخل الطبقة الحدية ولكن مع بقاء سرعة الجريان عند الجدار معدومة بسبب اللزوجة.
إذا نُظِر إلى توزع السرع في طبقة حدية صفيحية وأخرى مضطربة وُجِد أن تدرُّج توزع السرع عند سطح الجسم له قيمة أكبر في الطبقة الحدية المضطربة، كما هوواضح في الشكل (2)، مما يبين سبب زيادة الإجهاد المماسي τ0، وبالتالي زيادة مقاومة قوة الكبح التي يتعرض لها الجسم عندما تكون الطبقة الحدية مضطربة.
سماكة الطبقة الحدية
تدل الدراسات على أن سماكة الطبقة الحدية الصفيحية، والتي يرمز لها بـ δ، تعطى عند البعد x عن مقدمة الصفيحة بدلالة عدد رينولد Re تصغير|توزع السرع عند انفصال الطبقة الحدية وتدل التجارب على أن الطبقة الحدية تبقى صفيحية عندما تكون قيمة عدد رينولد أصغر من s3 × s103 وبعد ذلك تنقلب الطبقة الحدية إلى مضطربة.
انفصال الطبقة الحدية boundary layer separation
عند تعرض الجريان إلى تزايد في الضغط (dp/dx > 0) نتيجة لتغير شكل الجدار الذي يمر عليه السائل أولتغير المقطع الذي يمر عبره، فإن سرعة جريان السائل في الطبقة الحدية تتعرض إلى تباطؤ وارتفاع في الضغط وبالتالي يتغير توزع السرع
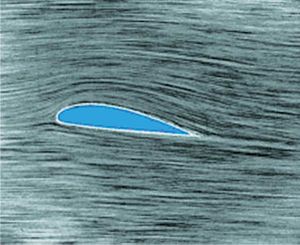
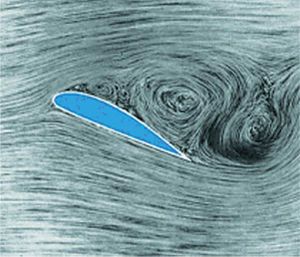
ما هوالحال في الشكل (4)، وتمثل هذه النقطة بداية ظهور جريان محلي يتجه باتجاه معاكس للجريان الأصلي مشكلاً دوّامة كما في الشكل (5)، دافعاً الطبقة الحدية النظامية إلى الخارج وعندئذ يجري الحديث عن انفصال الطبقة الحدية. وتترافق هذه الظاهرة مع ارتفاع كبير في قيمة الكبح الذي يتعرض له الجسم. ويعمل مهندسو الطيران جاهدين على تلافي ظهور هذه الظاهرة مهما كانت حالة الجريان.
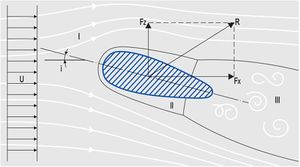
القوى المؤثرة على جسم يتعرض إلى جريان خارجي: عند تعرض جسم ما إلى جريان خارجي سرعته U يمكن تقسيم الجريان المحيط بالجسم إلى ثلاث مناطق بحسب الشكل (6):
I ـ منطقة الطبقة الحدية الصفيحية.
II ـ منطقة الطبقة الحدية المضطربة.
III ـ منطقة انفصال الجريان.
يولِّد الجريان في هذه المناطق الثلاث توزع إجهاد الاحتكاك وتوزع الضغط حول الجسم مشكلاً قوة احتكاك Fx في اتجاه الجريان وقوة رفع Fz عمودية على اتجاه الجريان.
الجريان الداخلي
عندما يدخل جريان منتظم سرعته U إلى أنبوب أوقناة تبدأ، نتيجة للزوجة السائل، طبقة حدية صفيحية بالتشكل مع تزايد في سماكتها إلى أن تحتل كامل مقطع الأنبوب في نهاية المرحلة الانتقالية التي يبلغ طولها Le يأخذ بعدها الجريان شكلاً صفيحياً مستقراً وله توزع سرع ثابت إذا لم يتجاوز عدد رينولد Re القيمة 2000.
نتيجة لتعرض السائل إلى احتكاك مماسي τ وإلى احتكاك مع جدار الأنبوب الداخلي tτ00 فإن هناك حاجة إلى قوة تدفع السائل عبر الأنبوب تغطي الطاقة الضائعة بالاحتكاك. وهذه القوة الدافعة هي فرق الضغط P1- P2 الواجب تطبيقه بين طرفي الأنبوب واللازم لتغطية فواقد الاحتكاك.
ويبرهن على أن توزع السرعة في أنبوب أسطواني يعطى بدلالة أبعاد الأنبوب وعامل لزوجة السائل
ويبرهن على أن توزع السرعة في أنبوب أسطواني يعطى بدلالة أبعاد الأنبوب وعامل لزوجة السائل μ بالعلاقة:العلاقة رقم (1)
وبمكاملة توزع السرع في مقطع الأنبوب نحصل على الغزارة Q المارة عبره مقدرة بالمتر المكعب في الثانية (m3/s).العلاقة رقم (2)
يلجأ مهندسو المياه إلى إعطاء هبوط الضغط بدلالة السرعة المتوسطة على شكل لا بعدي من خلال ثابت احتكاك الأنبوب lλ والمحدد بالعلاقة ويكون عندها:العلاقة رقم (3)
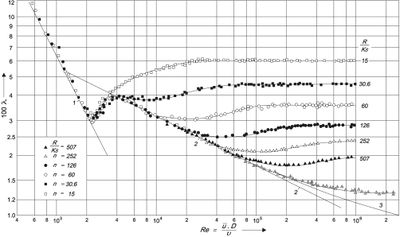
تدل التجارب على أن النتائج المذكورة أعلاه صحيحة عندما يكون عدد رينولد أصغر من 2300 أي عندما يكون الجريان صفيحياً وعندها يكون هبوط الضغط متناسباً مع مربع السرعة. وعندئذ تتعلق قيمة lλ بعدد رينولد فقط ولا يوجد أي تأثير لنعومة السطح الداخلي للأنبوب (الخط 1 من الشكل 8) أما إذا تجاوز عدد رينولد هذه القيمة فإن هبوط الضغط لا يبقى متناسباً مع السرعة بل مع مربعها بسبب تحول الجريان داخل الأنبوب إلى جريان مضطرب.
يعطى ثابت الاحتكاك lλ في حالة الجريان المضطرب والأنبوب الأملس (الخط2 وفق الشكل 9) بالعلاقة:العلاقة رقم (3)
أما في حالة الأنابيب الخشنة ذات الخشونة المطلقة متوسطة Ks والخشونة النسبية فإن ثابت الاحتكاك λ يصبح تابعاً لكل من عدد رينولد والخشونة النسبية وذلك عندما يكون عدد رينولد بين s3 ×s103 و s1 × s103 ويبقى ثابت الاحتكاك λ بعد ذلك تابعاً فقط للخشونة النسبية.
التأثير على الطبقة الحدية
يجهد مهندسو الطيران على إبقاء الطبقة الحدية صفيحية أطول مسافة ممكنة وذلك للإبقاء على المقاومة التي يتعرض لها الجسم صغيرة. وهناك عدة طرق للمحافظة على الطبقة الحدية صفيحية وتلافي تحوُّلها إلى مضطربة وتلافي انفصال الطبقة المضطربة لتشكل دوامات، ومن أهم هذه الطرق:
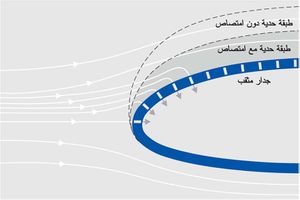
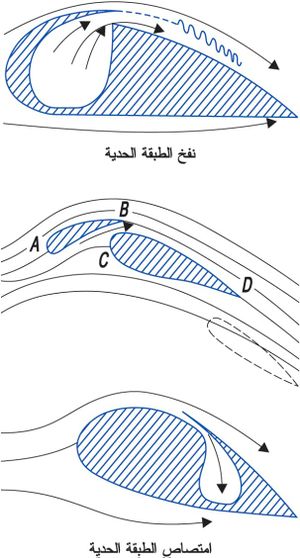
- امتصاص الطبقة الحدية من خلال شقوق أوثقوب صغيرة تتوضع على جدار الجسم يتم فيها امتصاص الطبقة الحدية وجعلها تلتصق بالجدار كما هوواضح في الشكل (9).
- نفخ الطبقة الحدية من خلال ضخ طبقة رقيقة من السائل بسرعة كبيرة في اتجاه الجريان مما يمنع انفصال الجريان كما يبين ذلك الشكل (10).
الطبقة الحدية في السرعات الصوتية
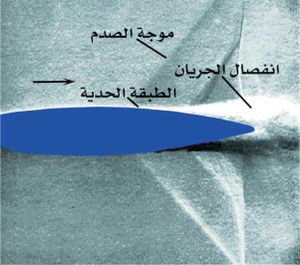
يرافق الجريان بسرعات صوتية ظهور ارتفاع مفاجئ في الضغط والكثافة ودرجة الحرارة نتيجة تحوُّل الجريان فوق الصوتي إلى جريان تحت صوتي مشكلاً موجة صدم shock wave. يؤدي تشكل موجة الصدم هذه إلى انفصال الطبقة الحدية وبالتالي إلى ارتفاع كبير في المقاومة التي يتعرض لها االجسم كما يظهر في الشكل (11)، لذا يلجأ مهندسو الطيران إلى انتقاء مقاطع لجناح الطائرة لا تسمح
أنظر أيضاً
- Boundary layer separation
- Boundary layer suction
- Boundary layer control
- Coandă effect
- Facility for Airborne Atmospheric Measurements
- Logarithmic law of the wall
- Planetary boundary layer
- Shape factor (boundary layer flow)
- Shear stress
المصادر
- Chanson, H. (2009). Applied Hydrodynamics: An Introduction to Ideal and Real Fluid Flows. CRC Press, Taylor & Francis Group, Leiden, The Netherlands, 478 pages. ISBN 978-0-415-49271-3.
{{cite book}}: External link in|title= - A.D. Polyanin and V.F. Zaitsev, Handbook of Nonlinear Partial Differential Equations, Chapman & Hall/CRC Press, Boca Raton - London, 2004. ISBN 1-58488-355-3
- A.D. Polyanin, A.M. Kutepov, A.V. Vyazmin, and D.A. Kazenin, Hydrodynamics, Mass and Heat Transfer in Chemical Engineering, Taylor & Francis, London, 2002. ISBN 0-415-27237-8
- Hermann Schlichting, Klaus Gersten, E. Krause, H. Jr. Oertel, C. Mayes "Boundary-Layer Theory" 8th edition Springer 2004 ISBN 3-540-66270-7
- John D. Anderson, Jr, "Ludwig Prandtl's Boundary Layer", Physics Today, December 2005
- Anderson, John (1992). Fundamentals of Aerodynamics (2nd edition ed.). Toronto: S.S.CHAND. pp. 711–714. ISBN 0-07-001679-8.
{{cite book}}:|edition=has extra text (help)
وصلات خارجية
- National Science Digital Library - Boundary Layer
- Moore, Franklin K., "Displacement effect of a three-dimensional boundary layer". NACA Report 1124, 1953.
- Benson, Tom, "Boundary layer". NASA Glenn Learning Technologies.
- Boundary layer separation
- Boundary layer equations: Exact Solutions - from EqWorld
- What is the Boundary Layer as it relates to Megasonic cleaning?